Adding Vector and Solving Vector Equations

Section 1.3 Adding Vector and Solving Vector Equations

Subsection 1.3.1 Adding Vectors

Subsubsection 1.3.1.1 Adding Vectors Component-by-Component

You can add vectors diagramatically or analytically. I will show first how to do it analytically using the coordinate-form of the vectors. Suppose you have two position vectors \(\vec r_1 \) and \(\vec r_2 \) and you want their sum \(\vec r_{\text{sum}} \text{.}\) Formally, we write this as a vector equation

\begin{equation} \vec r_{\text{sum}} = \vec r_1 + \vec r_2.\label{eq-vector-sum}\tag{1.3.1} \end{equation}

This is just a formal definition. THIS DOES NOT MEAN LENGTH OF THE SUM VECTOR IS EQUAL TO THE SUM OF THE LENGTHS OF THE TWO VECTORS BEING SUMMED!!!. Writing this definition of sum by coordinate representations of the three vectors, we might write it like the following.

\begin{equation*} \left( x_{\text{sum}}, x_{\text{sum}}\right) = (x_1, y_1) + (x_2, y_2). \end{equation*}

You will learn below that you can sum two vectors by placing one vector at the tip of the other vector and the sum will be from the tail of the first to the tip of the second. If you look at the diagram, you will immediately see that \(x_\text{sum}\) is just sum of \(x_1\) and \(x_2\text{,}\) and similarly for the \(y\) parts.

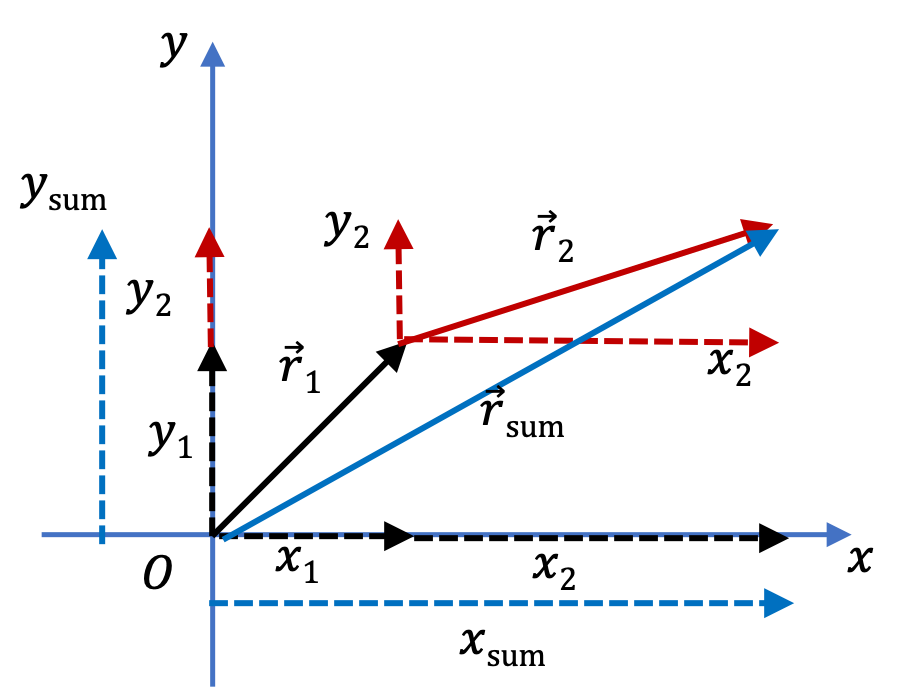
\begin{align} \amp x_{\text{sum}} = x_1 + x_2,\tag{1.3.2}\\ \amp y_{\text{sum}} = y_1 + y_2.\tag{1.3.3} \end{align}

Now, if we wanted the magnitude and direction of the sum vector, we can just use the \((x,y) \) to \((r, \theta)\) transformations, as we do for any vector.

\begin{align} \amp r_{\text{sum}} = \sqrt{ x_{\text{sum}}^2 + y_{\text{sum}}^2 }\tag{1.3.4}\\ \amp \tan \theta_{\text{sum}} = \dfrac{ y_{\text{sum}} }{ x_{\text{sum}} } \tag{1.3.5} \end{align}

Once we get the angle, we deduce the direction from the angle value based on the quadrant the vector is pointed, and then we state the direction as clockwise or counterclockwise angles from Cartesian axes.

Often a table of components helps organize the calculations. This is illustrated in Example 1.3.5.

Checkpoint 1.3.2. Adding Two Forces Given in Component Form.

Suppose a box is being pushed by two forces, which are given to us in component form, as \((F_x, F_y)\text{:}\)

\begin{equation*} \vec F_1 = (20\text{ N}, 25\text{ N}),\ \ \vec F_2 = (10\text{ N}, 15\text{ N}) \end{equation*}

What are the magnitude and direction of their sum, also called the net force, \(\vec F_{\text{net}}\text{.}\)

Hint

Add components first.

Answer

\(50\text{ N},\, 53.1^{\circ} \) counterclockwise from positive \(x \) axis.

Solution

From the discusssion of this section, we know that the components of the sum can be easily obtained from the components of the summand.

\begin{align*} \amp F_{\text{net},x} = F_{1x} + F_{2x} = 20\text{ N} + 10\text{ N} = 30\text{ N}. \\ \amp F_{\text{net},y} = F_{1y} + F_{2y} = 25\text{ N} + 15\text{ N} = 40\text{ N}. \end{align*}

Therefore, the magnitude of the sum is

\begin{equation*} \text{Magnitude, } F_{\text{net}} = \sqrt{30^2 + 40^2} = 50\text{ N}. \end{equation*}

To get the direction, we find the angle first by

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{40}{30}\right) = 53.1^{\circ}. \end{equation*}

Since point \((30, 40)\) is in the first quadrant, the direction of the net force is counterclockwise from the positive \(x \) axis.

Checkpoint 1.3.3. Adding Two Forces Given in Magnitude-Direction Form.

Suppose a box is being pushed by two forces, which are given to us in magnitude-direction form in the \(xy\) plane:

\begin{equation*} \vec F_1 = (30\text{ N},\, \text{East}),\ \ \vec F_2 = (40\text{ N},\, \text{South}) \end{equation*}

Use coordinate axes with positive \(x \) towards East and positive \(y \) towards North. What are the magnitude and direction of their sum? Note: magnitude is not equal to \(70\text{ N}\text{.}\)

Hint

First write the given forces in the component forms.

Answer

\(50\text{ N},\, 53.1^{\circ} \) clockwise from positive \(x \) axis.

Solution

We will need to first write the given forces in their component forms. Let \(x \) axis be towards East and the \(y \) axis towards North. Then, here the component forms of the two given forces are easy to work out.

\begin{align*} \amp \vec F_1 = (30\text{ N},\ 0),\\ \amp \vec F_2 = (0,\ -40\text{ N}) \end{align*}

Let's write \(\vec F \) for the sum vector. The components of the sum are then

\begin{align*} \amp F_{x} = F_{1x} + F_{2x} = 30\text{ N} + 0 = 30\text{ N}. \\ \amp F_{y} = F_{1y} + F_{2y} = 0 + (-40\text{ N}) = -40\text{ N}. \end{align*}

Therefore, the magnitude of the sum is

\begin{equation*} \text{Magnitude, } F_{\text{net}} = \sqrt{30^2 + 40^2} = 50\text{ N}. \end{equation*}

To get the direction, we find the angle first by

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{-40}{30}\right) = - 53.1^{\circ}. \end{equation*}

Since point \((30, -40)\) is in the fourth quadrant, the direction of the net force is clockwise from the positive \(x \) axis.

Checkpoint 1.3.4. Adding Two Force Vectors.

Consider two force vectors, \(\vec F_1 \) that has a magnitude \(25.0\text{ N}\) in the direction of East, and \(\vec F_2 \) that has a magnitude \(40.0\text{ N}\) in the direction of \(30^{\circ}\) North of East. What are the magnitude and direction of their sum, \(\vec F_1 + \vec F_2\text{?}\) For stating directions in space, let \(x \) axis be pointed towards East, \(y \) axis be pointed towards North, and \(z \) axis be pointed Up.

Hint

Add \(x \) components separately from the \(y \) components.

Answer

\(62.9\text{ N}, 18.6^{\circ} \) counterclockwise from East towards North.

Solution

First we find the component forms of each vector, and then will sum components in each direction separately.

\begin{align*} \amp F_{1x} = 25.0\text{ N},\ \ F_{1y} = 0,\\ \amp F_{2x} = 40.0 \cos\, 30^{\circ} = 34.6\text{ N}, \\ \amp F_{2y} = 40.0 \sin\, 30^{\circ} = 20.0\text{ N}, \end{align*}

Now, adding values along each axis separartely, we get \(x \) and \(y \) components of the sum. Let us denote them by \(F_x \) and \(F_y\text{.}\)

\begin{align*} \amp F_{x} = F_{1x} + F_{2x} = 25.0 + 34.6 = 59.6\text{ N},\\ \amp F_{y} = F_{1y} + F_{2y} = 20.0\text{ N}, \end{align*}

From these components, we can get the magnitude and direction. Since the values of \(F_x \) and \(F_y\) places the vector in the first quadrant, the angle will just be the counterclockwise from the positive \(x \) axis.

\begin{align*} \amp \text{Magnitude, }F = \sqrt{F_{x}^2 + F_{y}^2 } = \sqrt{59.6^2 + 20.0^2} = 62.9\text{ N},\\ \amp \theta = \tan^{-1}\left( \dfrac{F_y}{F_x} \right) = \tan^{-1}\left( \dfrac{20}{59.6} \right) = 18.6^{\circ}. \end{align*}

Example 1.3.5. Adding Forces Using an Organizing Table.

Suppose we want to add three forces shown in Figure 1.3.6.

(1) \(15.0\text{ N} \) force pointed down, (2) \(12\text{ N} \) force pointed \(54^{\circ}\) below horizon, and (3) \(10.0 \text{ N} \) force pointed up.

(a) Organize the components of these forces in a table and find the components of the sum.

(b) Find the magnitude and direction of the sum.

Hint

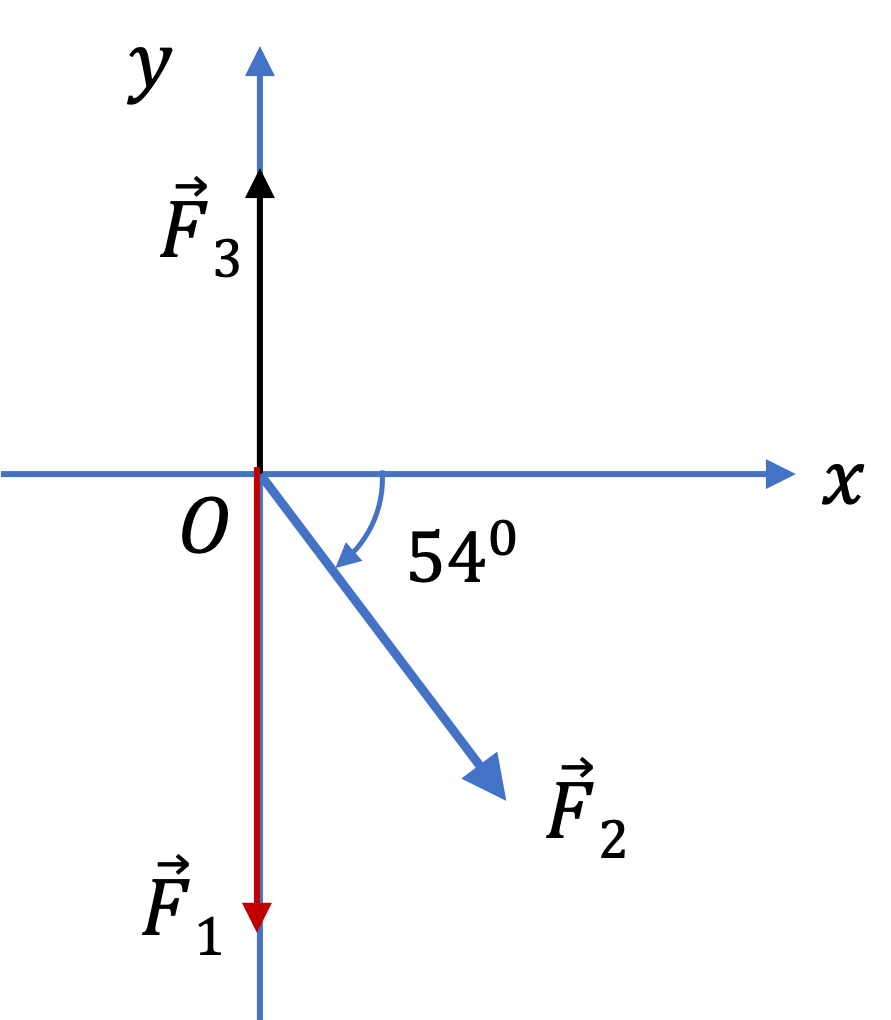
Find the components and make a table with three columns - name, \(x \) component, \(y\) component.

Answer 1 (a)

(a) \(( 7.05\text{ N}, -14.7\text{ N})\text{,}\)

Answer 2 (b)

(b) \(16.30\text{ N}, \) \(64.4^{\circ}\) clockwise from the positive \(x \) axis in the fourth quadrant.

Solution 1 (a)

We can make the following table to help us organize the components

Table 1.3.7. Force Components

Force	\(x\)-component	\(y\)-component
\(F_1 \)	\(0\)	\(-15.0\text{ N}\)
\(F_2 \)	\(12\text{ N}\, \cos\, 54^{\circ}=7.05\text{ N}\)	\(-12\text{ N}\, \sin\, 54^{\circ}=-9.71\text{ N}\)
\(F_3\)	0	\(10\text{ N}\)

From this table we find the components of the sum.

\begin{align*} \amp F_x = 0 + 7.05\text{ N} + 0 = 7.05\text{ N},\\ \amp F_y = -15.0\text{ N}-9.71\text{ N}+10\text{ N} = -14.7\text{ N}. \end{align*}

Solution 2 (b)

We use the components and find the magnitude to be

\begin{equation*} F = \sqrt{F_x^2 + F_y^2} = \sqrt{7.05^2 + 14.7^2 } = 16.30\text{ N}, \end{equation*}

and the angle with respect the the \(x \) axis

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{-14.7}{7.05} \right) = - 64.4^{\circ}, \end{equation*}

which means \(64.4^{\circ}\) clockwise from \(+x\) axis in the fourth quadrant.

Checkpoint 1.3.8. Adding Three Velocity Vectors.

Consider the following three velocity vectors:

\begin{align*} \amp \vec v_1 = \left(25.0\text{ m/s},\text{ towards East} \right), \\ \amp \vec v_2 = \left(25.0\text{ m/s},\ 30^{\circ}\text{ North of East} \right), \\ \amp \vec v_3 = \left(40.0\text{ m/s},\ 30^{\circ}\text{ North of West} \right). \end{align*}

What are the magnitude and direction of their sum, \(\vec v_1 + \vec v_2 + \vec v_3\text{?}\) For stating directions in space, let \(x \) axis be pointed towards East, \(y \) axis be pointed towards North, and \(z \) axis be pointed Up.

Hint

Be careful with the signs. The \(v_{3x} \) should be negative.

Answer

\(34.64\text{ m/s}, 69.7^{\circ} \)

Solution

We start by working out the components of each of the three velocity vectors. The components of \(\vec v_1 \) and \(\vec v_2 \) do not give us any trouble.

\begin{align*} \amp v_{1x} = 25.0\text{ m/s},\ \ v_{1y} = 0\\ \amp v_{2x} = 21.65\text{ m/s},\ \ v_{2y} = 12.5\text{ m/s} \end{align*}

However, we need to be careful when we work on \(\vec v_3 \) since the vector is pointed in the second quadrant of the \(xy \) plane. When we peoject the arrow of the vector \(\vec v_3 \) on the \(x \) axis, we strike the negative \(x \) axis, which means that \(v_{3x} \lt 0 \text{,}\) i.e., negative.

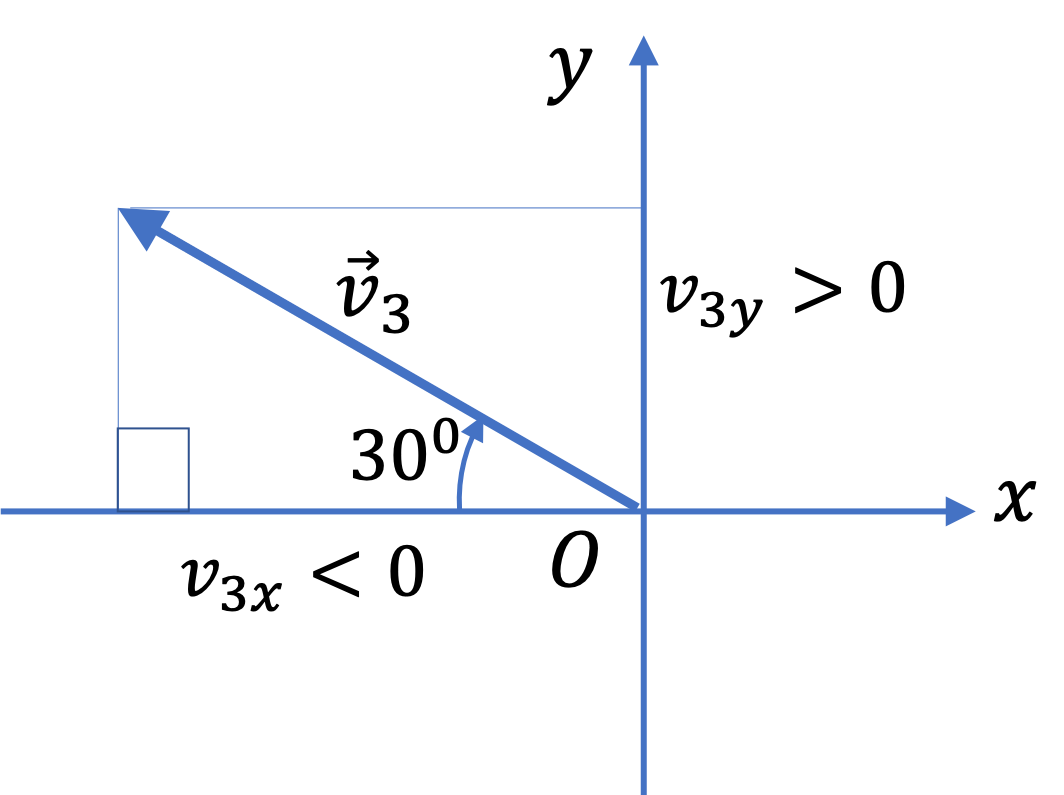
\begin{align*} \amp v_{3x} = -v_3\, \cos(|\theta|) = -34.64\text{ m/s}\\ \amp v_{3y} = +v_3\, \sin(|\theta|) = +20.0\text{ m/s} \end{align*}

The components of the sum, to be written as \(v_x \) and \(v_y\) will be

\begin{align*} \amp v_{x} = v_{1x} + v_{2x} + v_{3x} = 25.0+21.65-34.64 = 12.0\text{ m/s},\\ \amp v_{y} = v_{1y} + v_{2y} + v_{3y} = 0 + 12.5 + 20 = 32.5\text{ m/s}. \end{align*}

This results in the following magnitude and angle

\begin{align*} \amp v = \sqrt{v_{x}^2 + v_y^2} = 34.64\text{ m/s},\\ \amp \theta = \tan^{-1}\left( \dfrac{v_y}{v_x}\right) = 69.7^{\circ}. \end{align*}

Subsubsection 1.3.1.2 Adding Vectors Diagramatically

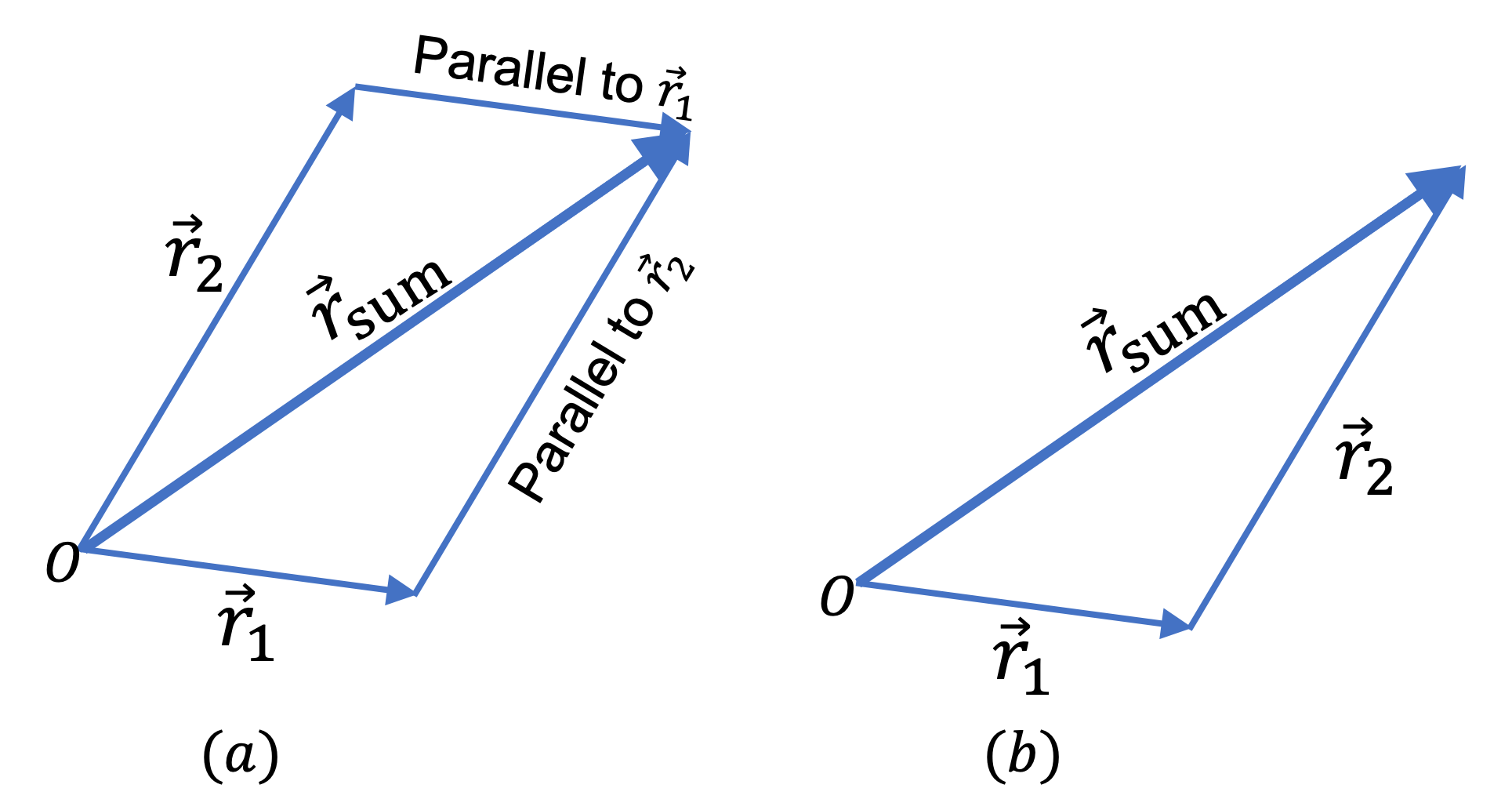
In diagram form, the sum \(\vec r_{\text{sum}}\) is the diagonal vector in the parallelogram constructed from \(\vec r_1\) and \(\vec r_2\) when \(\vec r_1\) and \(\vec r_2\) are drawn from the same point as shown in Figure 1.3.10(a). This is called the parallelogram law of addition.

An alternative view of vector addition by a diagram is shown in Figure 1.3.10(b). Here, we move the second vector so that it starts at the tip of the first vector. Then, the vector from the tail of the first vector to the tip of the second vector would be the same as the diagonal of the corresponding parallogram, and hence would be the sum of the two vectors. This method is often called tip-to-tail method of addition.

Figure 1.3.10. Illustrating vector sum, \(\vec r_{\text{sum}} = \vec r_1 + \vec r_2\text{.}\) (a) The Parallelogram View: Form a paralleogram from \(\vec r_1\) and \(\vec r_2\text{,}\) then the diagonal will be the sum \(\vec r_{\text{sum}}\text{.}\) (b) The Triangle View: Place the tail of vector \(\vec r_2\) at the tip of vector \(\vec r_1\text{,}\) then the sum is the vector from the tail of \(\vec r_1\) to the tip of \(\vec r_2\text{.}\)

Checkpoint 1.3.11. Adding Vectors Graphically.

(a) From Figure 1.3.12 , read off magnitudes and directions of vectors \(\vec A \) and \(\vec B \text{,}\) draw the negative of vector \(\vec B \text{.}\) Lets call it \(\vec C\text{.}\)

(b) Find the magnitude and direction of \(\vec A - \vec B\) in two ways: (i) from the components of \(\vec A + \vec C\text{,}\) and (ii) graphically from the parallelogram formed by \(\vec A \) and \(\vec C \text{.}\)

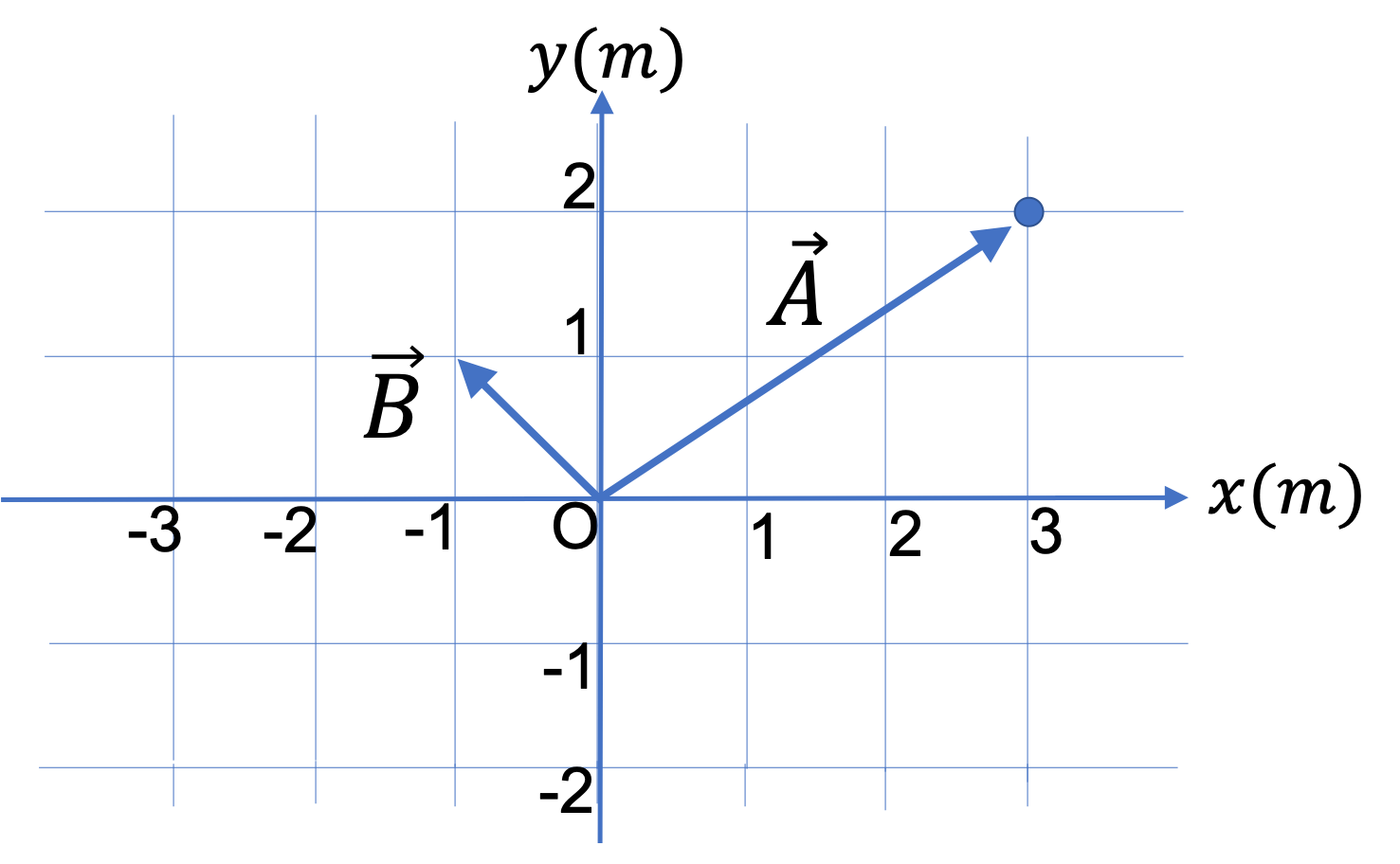
Figure 1.3.12. Figure for Checkpoint 1.3.11.

Hint

For (b) (i), read off the components of \(\vec A \) and \(\vec B \) and then work out the algebra. For (b) (ii), us a ruler to read off the length of the vector and a protractor to read the angle.

Answer

(b) (i) \(\sqrt{17}\text{ m}, 14.0^{\circ} \) counterclockwise from \(+x\) axis.

Solution 1 (a)

(a) We first draw vector \(\vec C\) as shown in Figure 1.3.13.

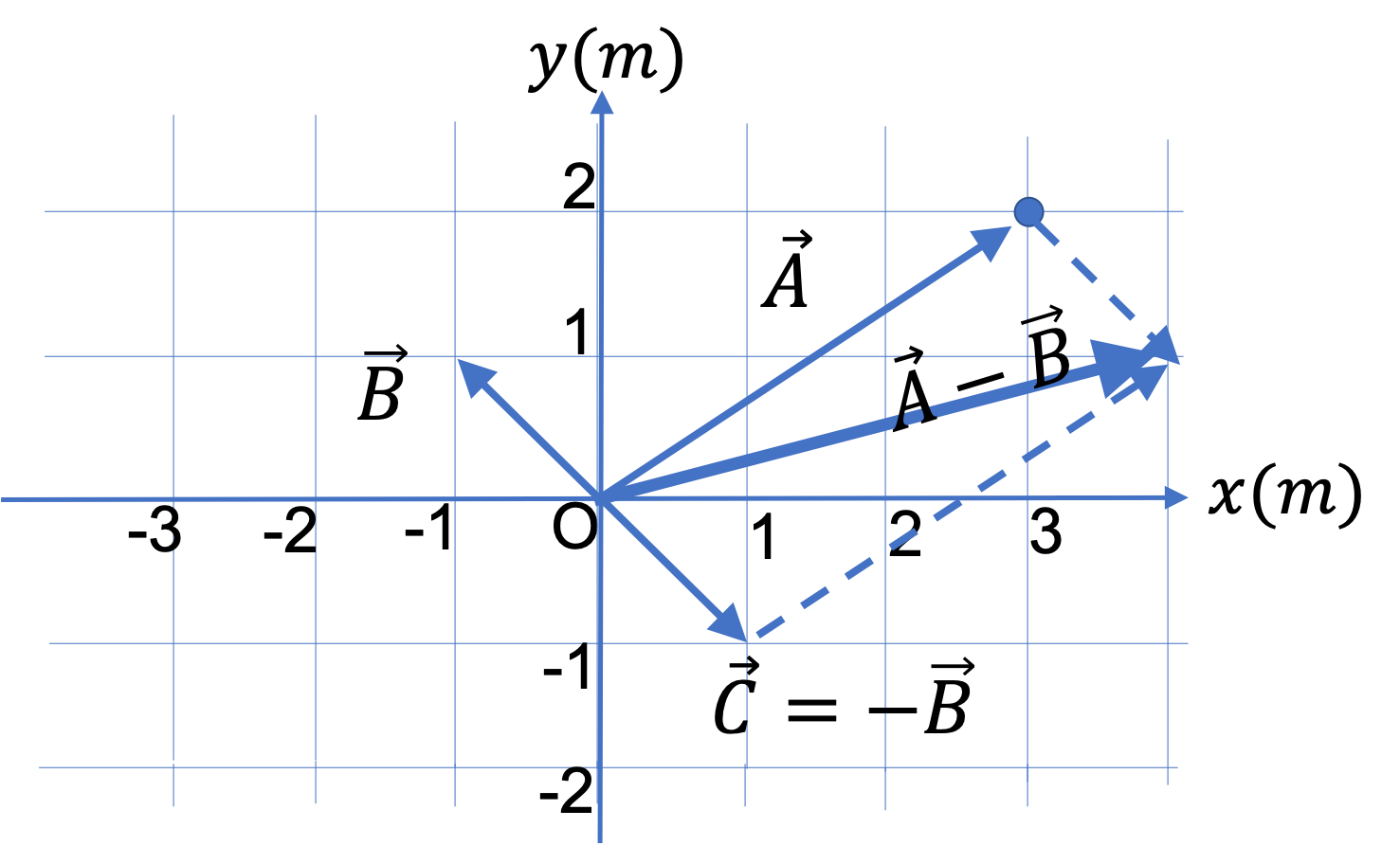
Figure 1.3.13. Figure for Checkpoint 1.3.11(a).

Solution 2 (b)

(b) (i) We add \(\vec A \) and \(\vec C\) using their components. Let's denote the sum by \(\vec D\text{.}\)

\begin{align*} \amp D_x = A_x + C_x = 3 + 1 = 4.\\ \amp D_y = A_y + C_y = 2 - 1 = 1. \end{align*}

Therefore, the magnitude and angle are:

\begin{align*} \amp D = \sqrt{D_x^2 + D_y^2 } = \sqrt{17}\text{ m}.\\ \amp \theta = \tan^{-1}\left( \dfrac{1}{4}\right) = 14.0^{\circ}. \end{align*}

Since \((4,1) \) is in the first quadrant, the direction is this angle counterclockwise from the positive \(x \) axis.

(b) (ii) I printed out the figure and used a ruler and a protractor to get the length and the angle - this will give only approximate values, and that's okay. Read directly, the magnitude is \(\approx 4.0 \) and the counterc;ockwise angle from the positive \(x \) axis is \(\approx 15^{\circ}\text{.}\) These values are close enough to the exact values in (i).

Subsection 1.3.2 Solving Vector Equations

The sum equation, Eq. (1.3.1), viz., \(\vec r_\text{sum} = \vec r_1 + \vec r_2\text{,}\) is an example of a vector equation, where the left and right sides of the equation are vector quantites written in abstract formal symbols. In the coordinate forms of the vectors, we saw that \(x \) components come together separately from the \(y \) components and resulted in simple algebraic equations for \(x\) and \(y\) components.

Simplest vector equation will have two vectors that are equal to each other. For example

\begin{equation*} \vec A = \vec B. \end{equation*}

What this is saying is that the two vectors have the same magnitude and the same direction.

\begin{align*} \amp A = B, \text{ and } \\ \amp \text{Direction of }\vec A = \text{Direction of }\vec B \end{align*}

If we look at the components of \(\vec A \) and \(\vec B \text{,}\) we will conclude that, they have the same components.

\begin{equation} A_x = B_x,\ \ A_y = B_y,\ \ A_z = B_z. \label{eq-vector-equation-component}\tag{1.3.6} \end{equation}

A more general example of a vector equation will be

\begin{equation*} \vec A + \vec B = \vec C + \vec D. \end{equation*}

This will give us the following three equations for the components.

\begin{align*} \amp A_x + B_x = C_x + D_x, \\ \amp A_y + B_y = C_y + D_y, \\ \amp A_z + B_z = C_z + D_z. \end{align*}

Checkpoint 1.3.14. Negative of a Vector.

Two vectors \(\vec A \) and \(\vec B \) add up to give a zero vector. Suppose vector \(\vec A \) is known, what can you say about the magnitude and direction of vector \(\vec B\text{?}\)

Hint

Think what happens when you change the sign of a vector

Answer

\(B = A\text{,}\) opposite direction of \(\vec A\text{.}\)

Solution

We are given that

\begin{equation*} \vec A + \vec B = 0. \end{equation*}

Solving for \(\vec B \text{,}\) we get

\begin{equation*} \vec B = - \vec A. \end{equation*}

That is, \(\vec B \) is just \(\vec A \) woith direction flipped. Therefore, \(\vec B \) has the same magnitude as \(\vec A \) but has opposite direction

Checkpoint 1.3.15. Finding the Third Force that will Balance Two Other Forces Given in Component Form.

Consider a situation in which three forces cancel out. Two of the forces are given in the component form in the \(xy\)-plane as \(\vec F_1 = (20 \text{ N}, 10 \text{ N}) \text{,}\) and \(\vec F_2 = (-30 \text{ N}, 10 \text{ N}) \text{.}\)

(a) What are the magnitude and direction of the third force? (b) Draw the three forces in the tip-to-tail manner and show that they form a closed path.

Hint

(a) Thinking in terms of components is helpful. (b) Why would they form a closed path? Think what their sum is.

Answer

(a) \((10\text{ N} , -20 \text{ N}) \) in component form, giving magnitude \(10\sqrt{5}\text{ N} \text{,}\) and the angle, \(\theta = 63.4^\circ\) clockwise into the fourth quadrant.

Solution 1 (a)

(a) Let us call the third force \(\vec F_3 \text{.}\) Then, we are given that

\begin{equation*} \vec F_1 + \vec F_2 + \vec F_3 = 0. \end{equation*}

Therefore,

\begin{equation*} \vec F_3 = -( \vec F_1 + \vec F_2 ), \end{equation*}

which means, the components of \(\vec F_3\) will be opposite of those of the sum of the other two force. Hence, (note: as in other places, we omit units in calculations, but put the units back in the final result.)

\begin{align*} \amp F_{3x} = -( F_{1x} + F_{2x} ) = -( 20 -30) = 10\text{ N}.\\ \amp F_{3y} = -( F_{1y} + F_{2y} ) = -( 10 + 10) = -20\text{ N}. \end{align*}

Therefore the magnitude and angle of \(\vec F_3 \) are

\begin{align*} \amp F = \sqrt{F_{3x}^2 + F_{3y}^2} = \sqrt{10^2 + 20^2} = 22.4\text{ N}.\\ \amp \theta = \tan^{-1}\left(\dfrac{F_{3y}}{F_{3x}} \right) = -63.4^{\circ}. \end{align*}

Since \((F_{3x} , F_{3y}) = (10, -20) \) in the fourth quadrant, the direction is \(63.4^{\circ}\) clockwise from positive \(x \) axis.

Solution 2 (b)

The three forces placed tip-to-tail should form a closed loop for their vector sum to be zero. We draw \(\vec F_1\) and \(\vec F_2\) to scale, and then find \(\vec F_3\) from the tip of \(\vec F_2\) to the tail of \(\vec F_1\text{.}\)

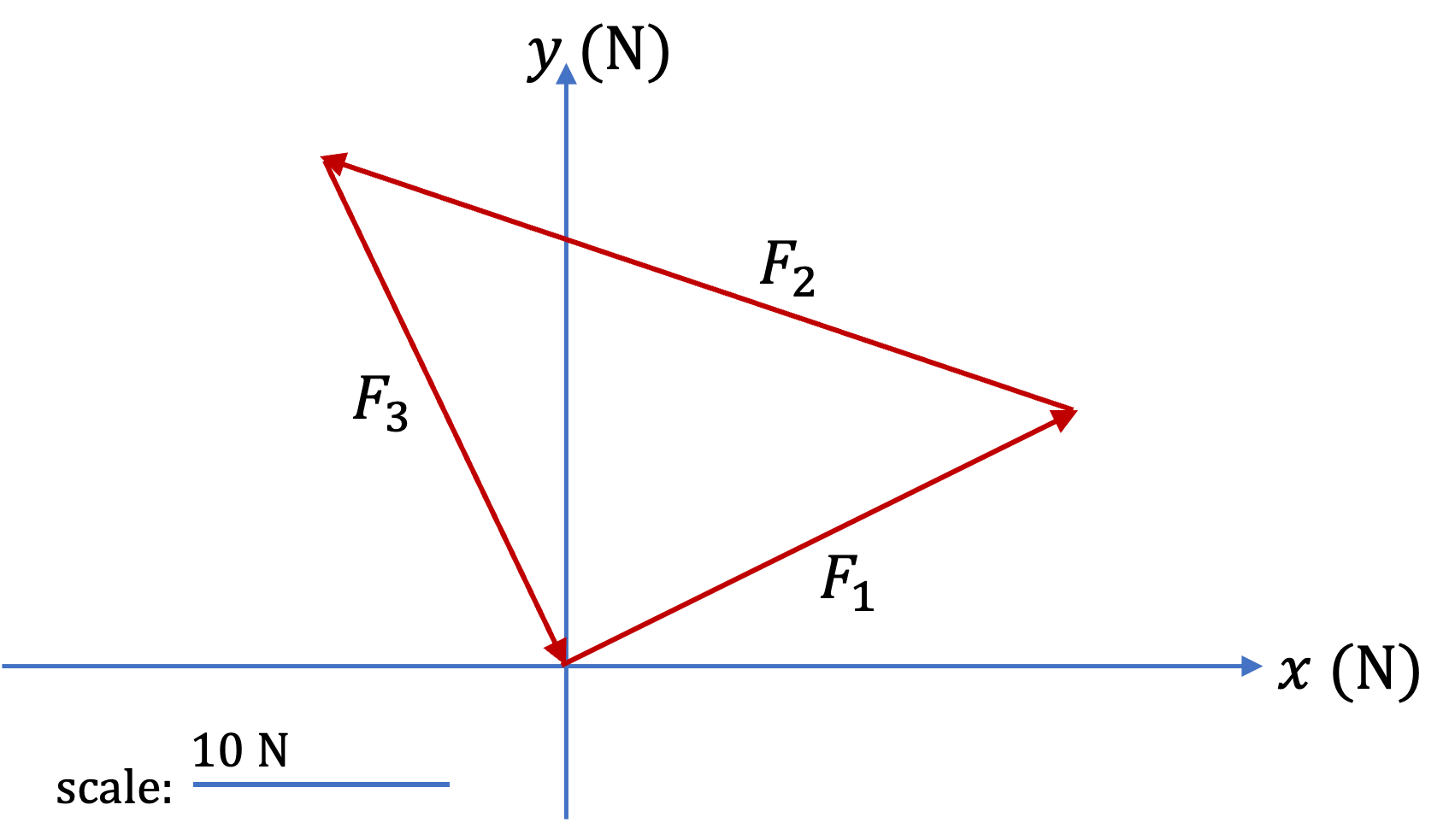
Checkpoint 1.3.17. Finding the Third Force that will Balance Two Other Forces Given in Magnitude-Direction Form.

Consider a situation in which three forces cancel out, i.e., their vector sum is equal to zero. Two of the forces are: \(\vec F_1 = (12\) N, due East), and \(\vec F_2 = (5\) N, due North).

(a) What are the magnitude and direction of the third force?

(b) Draw the three forces in the tip-to-tail manner and show that they form a closed path. Why would they form a closed path? Hint: Think about their sum.

Hint

Convert the given forces to component form first.

Answer

(a) \((-12\text{ N} , -5 \text{ N}) \) in component form with \(x \) towards East and \(y \) toward North. This will give magnitude = \(13 \text{ N}\text{,}\) and the angle will be in the third quadrant, \(22.6^\circ\) south of west.

Solution

(a) Let us call the third force \(\vec F_3 \text{.}\) Then, we are given that

\begin{equation*} \vec F_1 + \vec F_2 + \vec F_3 = 0. \end{equation*}

Therefore,

\begin{equation*} \vec F_3 = -( \vec F_1 + \vec F_2 ), \end{equation*}

which means, the components of \(\vec F_3\) will be opposite of those of the sum of the other two force. From the magnitudes and directions of \(\vec F_1 \) and \(\vec F_2 \) we find their component forms to be

\begin{align*} \amp F_{1x} = 12\text{ N},\ \ F_{1x} = 0,\\ \amp F_{2x} = 0,\ \ F_{1x} = 5\text{ N}, \end{align*}

Therefore, for \(\vec F_3 \) we get

\begin{align*} \amp F_{3x} = -( F_{1x} + F_{2x} ) = -( 12 + 0) = -12\text{ N}.\\ \amp F_{3y} = -( F_{1y} + F_{2y} ) = -( 0 + 5) = -5\text{ N}. \end{align*}

Therefore the magnitude and angle of \(\vec F_3 \) are

\begin{align*} \amp F = \sqrt{F_{3x}^2 + F_{3y}^2} = \sqrt{12^2 + 5^2} = 13.0\text{ N}.\\ \amp \theta = \tan^{-1}\left(\dfrac{F_{3y}}{F_{3x}} \right) = \tan^{-1}\left(\dfrac{ -5}{-12}\right) = 22.6^{\circ}. \end{align*}

Since \((F_{3x} , F_{3y}) = (-12, -5) \) in the third quadrant, the direction is \(22.6^{\circ}\) counterclockwise from the negative \(x \) axis. This is \(22.6^{\circ}\) South of West.