Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 3.9 Vectors Bootcamp

Exercises Exercises

Vectors as Arrows

2. Three Forces Acting at Three Points on a Ring.
Follow the link: Example 3.10.
3. Three Forces Acting at Three Points on a Ring.
Follow the link: Exercise 3.1.9.2.

Representing Vectors

6. Find Unit Vector in the Direction of a Given Vector.
Follow the link: Example 3.30.
7. Magnitude and Direction of a Vector in 2D from Components.
Follow the link: Exercise 3.2.5.1.
8. Components of a Vector from Magnitude and Direction in 2D.
Follow the link: Exercise 3.2.5.2.
9. Components of Velocity Vector of a Cricket Ball in a Horizontal-Vertical Plane.
Follow the link: Exercise 3.2.5.3.
10. Components of Velocity Vector of a Soccer Ball in a Horizontal-Vertical Plane.
Follow the link: Exercise 3.2.5.4.
11. Magnitude and Direction of Velocity from Components.
Follow the link: Exercise 3.2.5.5.
12. Magnitude and Direction of Velocity from Components - 2.
Follow the link: Exercise 3.2.5.6.
13. Magnitude and Direction of Force.
Follow the link: Example 3.56.
14. Practice Computing Magnitudes and Stating Directions.
Follow the link: Exercise 3.2.5.8.
15. Components of a Force Vector from Magnitude and Direction in First Quadrant.
Follow the link: Exercise 3.2.5.7.
16. Direction in the Second Quadrant.
Follow the link: Example 3.58.
17. Direction in the Third Quadrant.
Follow the link: Example 3.61.
18. Direction in the Fourth Quadrant.
Follow the link: Example 3.64.
19. Components of a Force Vector from Magnitude and Direction in the Fourth Quadrant.
Follow the link: Exercise 3.2.5.9.
20. Magnitude and Direction of a Force Vector from Components in the Second Quadrant.
Follow the link: Exercise 3.2.5.10.
21. Unit Vector in an an Arbitrary Direction.
Follow the link: Example 3.51.
22. Draw Vectors Written in Component Form.
Follow the link: Example 3.42.
23. Find Components of a Vector in Two Frames.
Follow the link: Example 3.46.
26. Angle Vectors Make with the Cartesian Axes.
Follow the link: Example 3.50.
27. Practice with a Friend: Angles Vectors Make with Cartesian Axes.
Follow the link: Exercise 3.2.5.15.

Adding Vectors

29. Adding Two Forces Given in Component Form.
Follow the link: Example 3.79.
30. Adding Two Forces Given in Magnitude-Direction Form.
Follow the link: Example 3.80.
35. Finding the Third Force that will Balance Two Other Forces Given in Component Form.
Follow the link: Exercise 3.4.1.
36. Finding the Third Force that will Balance Two Other Forces Given in Magnitude-Direction Form.
Follow the link: Exercise 3.4.2.

Multiplying Vectors

39. Scalar Product of Two Vectors Given in Components.
Follow the link: Example 3.88.
40. Scalar Product of Two Vectors Given Magnitudes and Directions.
Follow the link: Example 3.89.
41. Finding Angle Between Two Vectors.
Follow the link: Example 3.90.
45. Unit Vectors in the Direction of Perpendicular to a Given Vector.
Follow the link: Exercise 3.5.4.
48. Magnetic Force on a Current Carrying Wire.
Follow the link: Example 3.93.
49. Cross Product Using Components of Vectors.
Follow the link: Example 3.92.
50. Computing Dot and Cross Products of Displacement and Force Vectors.
Follow the link: Exercise 3.6.3.
51. Computing Dot and Cross Products of Displacement and Force Vectors.
Follow the link: Exercise 3.6.4.
52. Dot and Cross Products of Perpendicularly Directed Vectors.
Follow the link: Exercise 3.6.6.
53. Unit Vector in the Direction of a Vector.
Follow the link: Example 3.53.

Miscellaneous

54. Unit Vector Perpendicular to the Body Diagonal of a Cube.
(a) Using origin at the corner at the tail of the body diagonal shown in Figure 3.99 and a right-handed Cartesian axes along the edges of the cube, write an analytic expression for the unit vector along the body diagonal.
(b) Find a unit vector that is perpendicular to the body diagonal.
Figure 3.99. Exercise 3.9.54.
Solution 1. a
Let \(\vec R\) be the bodydiagonal vector. This will be
\begin{equation*} \vec R = a\,\hat u_x + a\,\hat u_y + a\,\hat u_z. \end{equation*}
Now, we divide i=by its magnitude to get a unit vector in this direction. Let us denote it by \(\hat u_R\text{.}\)
\begin{equation*} \hat u_R = \frac{a\,\hat u_x + a\,\hat u_y + a\,\hat u_z}{\sqrt{a^2 + a^2 + a^2}} = \frac{1}{\sqrt{3}}\left( \hat u_x + \hat u_y + \hat u_z\right). \end{equation*}
Solution 2. b
Let us denote an arbitrary vector perpendicular to \(\vec R\) by \(\vec N\text{.}\) Then,
\begin{equation} \vec R \cdot \vec N = 0.\tag{3.36} \end{equation}
A unit vector in the direction of \(\vec N\) will simply be equal to the vector \(\vec N\) divided by the magnitude of this vector.
Putting \(\vec R = a \hat u_x + a \hat u_y + a \hat u_z\) in Eq. (3.36) gives the following equation for the components of the normal we seek.
\begin{equation*} N_x + N_y + N_ z = 0. \end{equation*}
There are infinitely many answer to the given problem since any vector in the plane perpendicular to the body diagonal will be perpendicular to the vector along the body diagonal. For instance, one such vector will have \(N_x = 1\text{,}\) \(N_y = -1\) and \(N_z = 0\text{,}\) which is the vector \(\hat u_x - \hat u_y\text{.}\)
55. Angle Between Corners of One Edge and the Center of Opposite Face of a Cube.
Find the angle between the lines from the center of one face to the corners on the opposite face of a cube.
Figure 3.100. Exercise 3.9.55.
Solution.
From the coordinates of the three points O, P and Q we can determine analytic representations of the two vectors between which we seek the angle.
\begin{align*} \amp\overrightarrow{OQ} = \frac{1}{2}\hat u_x + \hat u_y + \frac{1}{2}\hat u_z\\ \amp\overrightarrow{PQ} = -\frac{1}{2}\hat u_x + \hat u_y + \frac{1}{2}\hat u_z \end{align*}
The cosine the angle \(\theta\) between the two vectors is related to the dot product between the two.
\begin{equation*} \cos\theta = \frac{\overrightarrow{OQ} \cdot \overrightarrow{PQ}}{|\overrightarrow{OQ}|\ |\overrightarrow{PQ}| } = \frac{1}{\sqrt{3/2}\sqrt{3/2}} = \frac{2}{3}. \end{equation*}
Therefore, the angle between the two vectors is \(\cos^{-1}(2/3)\text{.}\)
56. Angle Between Two Body Diagonals of a Cube.
Two body diagonals of a cube cross at the center of the cube. Find the angle between them.
Solution.
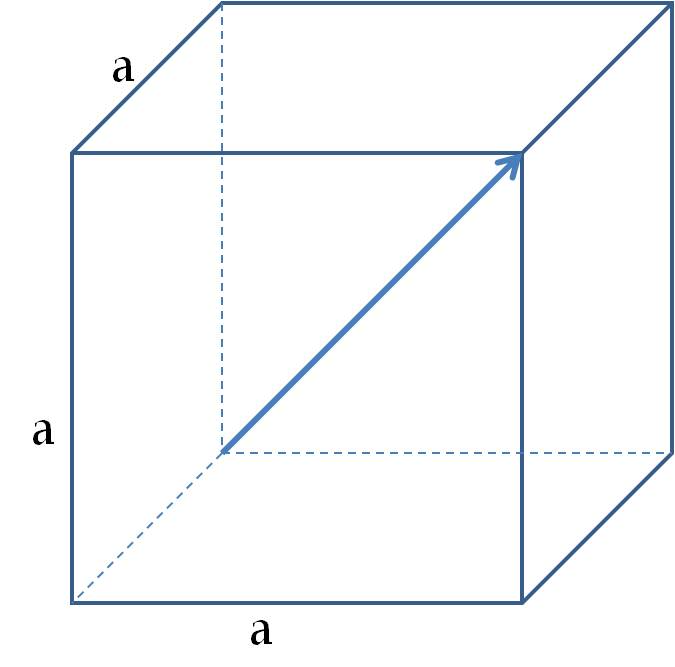
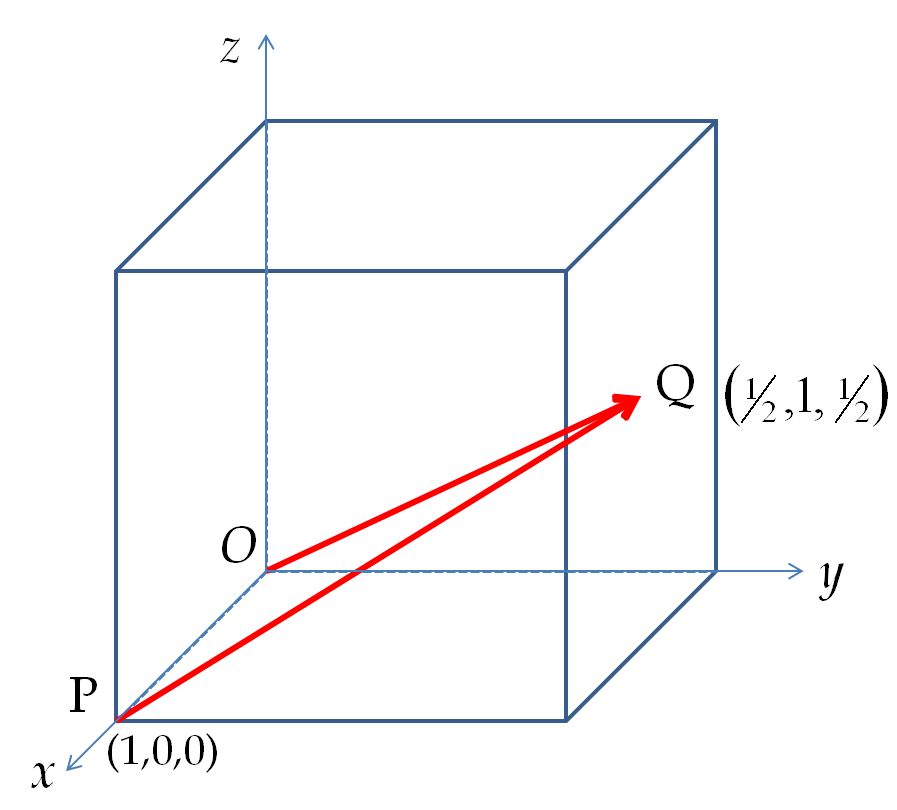
Two opposite corners of a cube make a body diagonal. There will be four body diagonals connecting the opposite corners to which there will correspond the following vectors (the negative of these vectors will work also).
\begin{align*} \amp \vec d_1 = \left[ (0,0,0) \rightarrow (1,1,1)\right] = \hat u_x + \hat u_y + \hat u_z\\ \amp \vec d_2 = \left[ (1,0,0) \rightarrow (0,1,1)\right] = - \hat u_x + \hat u_y + \hat u_z\\ \amp \vec d_3 = \left[ (0,1,0) \rightarrow (1,0,1)\right] = \hat u_x - \hat u_y + \hat u_z\\ \amp \vec d_4 = \left[ (0,0,1) \rightarrow (1,1,0)\right] = \hat u_x + \hat u_y - \hat u_z \end{align*}
I will work out the angle between \(\vec d_1\) and \(\vec d_2\) and you can practice with the others.
\begin{equation*} \cos\theta = \frac{\vec d_1 \cdot \vec d_2}{|\vec d_1|\ |\vec d_2|} =\frac{1}{\sqrt{3}\ \sqrt{3}} = \frac{1}{3}. \end{equation*}
Therefore, the angle between the two vectors is \(\cos^{-1}(1/3)\text{.}\)
57. Volume of a Parallelopiped.
(a) A parallelopiped can be described by stating three vectors along its edges as shown in Figure 3.101. Just as area of the base here could be obtained from the magnitude of vector product \(|\vec B \times \vec C|\text{,}\) the volume of the parallelopiped can be obtained by a scalar triple prroduct.
\begin{equation*} \vec A \cdot (\vec B \times \vec C). \end{equation*}
Prove that volume is indeed given by this formula.
Figure 3.101. For Exercise 3.9.57.
(b) Also show that you get the same answer by cyclically rotating the vector names, e.g.,
\begin{equation*} \vec A \cdot (\vec B \times \vec C) = \vec B \cdot (\vec C \times \vec A) = \vec C \cdot (\vec A \times \vec B). \end{equation*}
Solution 1. a
We will not do the full blown proof. We will assume that the area of the base times height equals the volume.
We will now show that \(\vec A\cdot ( \vec B \times \vec C)\) is equal to the area of the base times height.
Let’s start with noting that the magnitude of the cross-product \(\vec B \times \vec C\) is equal to the area of the base whose edges are the vectors \(\vec B\) and \(\vec C\) and the direction of this product is normal to the area.
Denote the normal direction to the base in which vectors \(\vec B\) and \(\vec C\) reside by the unit vector \(\hat u_n\text{.}\) Now, the dot product between \(\vec A\) and \(\hat u_n\) will equal the magnitude of the projection of vector \(\vec A\) on the normal direction, which is equal to the height.
Therefore, \(\vec A\cdot ( \vec B \times \vec C)\) would be equal to the product of the area of the base and the height, which is equal to the volume.
Solution 2. b
\begin{align*} \amp \vec A\cdot ( \vec B \times \vec C )\\ \amp \ \ \ = A_x (B_y C_z - B_z C_y) + A_y (B_z C_x - B_x C_z) + A_z (B_x C_y - B_y C_x) \end{align*}
We can rearrange the result now by grouping terms with \(B_x\text{,}\) \(B_y\) and \(B_z\) separately. We find that
\begin{align*} \amp A_x (B_y C_z - B_z C_y) + A_y (B_z C_x - B_x C_z) + A_z (B_x C_y - B_y C_x)\\ \amp \ \ = B_x (C_y A_z - C_z A_y) + B_y (C_z A_x - C_x A_z) + B_z (C_x A_y - C_y A_x)\\ \amp \ \ = \vec B\cdot ( \vec C \times \vec A ). \end{align*}
Similarly by arranging terms with \(C_x\text{,}\) \(C_y\) and \(C_z\) separately we can show that the result is also equal to \(\vec C\cdot ( \vec A \times \vec B )\text{.}\)
58. Prove the Law of Cosine.
In a triangle \(\triangle ABC \text{,}\) let \(a,\, b,\) and \(c \) denote the lengths of the sides, and C denote the angle between sides \(a\) and \(b\text{.}\) Use vector concepts to prove the following relation.
\begin{equation*} c^2 = a^2 + b^2 -2\, a\, b\, \cos\, C. \end{equation*}
Hint.
Use a triangle of vectors oriented such that \(\vec c = \vec a + \vec b \text{.}\)
Answer.
In the problem statement.
Solution.
Consider a triangle of vectors along the sides of the triangle as shown in Figure 3.102. From this figure, we get the following vector relation.
\begin{equation*} \vec c = \vec a + \vec b. \end{equation*}
Figure 3.102. The arrows on the sides show that \(\vec c = \vec a + \vec b\text{.}\) The angle \(\theta\) between the vectors \(\vec a \) and \(\vec b\) is the angle when the tails of both of these vectors are at the same place, as obtained by redrawing vector \(\vec a \) shown. the redrawing shows that \(\theta = 180^{\circ} -C\text{.}\)
Now, taking the dot product of each side with itself, we get
\begin{equation} \vec c \cdot \vec c = \vec a \cdot \vec a + \vec b \cdot \vec b + 2\vec a \cdot \vec b.\tag{3.37} \end{equation}
We can rewrite the last term in terms of the angle between vectors \(\vec a\) and \(\vec b \text{,}\) which is just \(180^{\circ} -C\text{.}\) Therefore,
\begin{equation*} \vec a \cdot \vec b = a\, b\, \cos(180^{\circ} -C) = -a\, b\, \cos\,C. \end{equation*}
Using this in Eq. (3.37) gives the result we seek.
\begin{equation*} c^2 = a^2 + b^2 -2\, a\, b\, \cos\, C. \end{equation*}
59. Prove the Law of Sines.
In a triangle \(\triangle ABC \text{,}\) let \(a,\, b,\) and \(c \) denote the lengths of the sides, and A, B, C denote the angles opposite to the corresponding sides as shown in the figure. Use vector concepts to prove the following relations.
\begin{equation*} \dfrac{\sin\, A}{a} = \dfrac{\sin\, B}{b} = \dfrac{\sin\, C}{c}. \end{equation*}
Hint.
Examine height of the triangle.
Answer.
In the problem statement.
Solution.
Look at the construction in the figure below, where height from the tip with angle \(\langle A \) to the the (extended) base on the other side is shown.
Since
\begin{equation*} \sin\left( 180^{\circ} -C \right) = \sin\, C, \end{equation*}
equating the two expressions for the height gives
\begin{equation*} c\, \sin\, B = b\, \sin\, C. \end{equation*}
Therefore,
\begin{equation*} \dfrac{\sin\, B}{b} = \dfrac{\sin\, C}{a}. \end{equation*}
Similar construction from the tip at angle \(\langle C \) will show
\begin{equation*} \dfrac{\sin\, A}{a} = \dfrac{\sin\, B}{b}. \end{equation*}
The two equations taken together prove the statement of the law of sines.
60. Relative Velocity.
Suppose you and your friend are on a large ship. Suppose the ship has a velocity of \(3 \) m/s pointed towards the positive \(x \) axis as seen from the shore. Suppose your friend is moving with respect to you (i.e., the ship) at a velocity of \(4 \) m/s towards the positive \(y \) axis. What is your friend’s velocity vector with respect to the shore. Find both component, and the magnitude and direction forms.
Note that a good notation will help. For instance, we can label each velocity with two subscripts, one for the object and the second the object with respect to which we have that velocity. Thus, let \(\vec v_{SG} \) will be velocity vector of the ship with respect to the ground. This is given in componen form, \(\vec v_{SG} = (3 \text{ m/s}, 0)\) in the \(xy\)-plane. Similarly, \(\vec v_{FS} = (0, 4 \text{ m/s})\text{.}\) And, we want \(\vec v_{FG} \text{.}\)
Hint.
Use \(\vec v_{FG} = \vec v_{FS} + \vec v_{SG}\text{.}\)
Answer.
\(5 \text{ m/s at } 53.1^{\circ} \text{ counterclockwise from } +x \text{ axis}.\)
Solution.
The relation between velocities, as seen in the figure provided, can be formally written as
\begin{equation*} \vec v_{FG} = \vec v_{FS} + \vec v_{SG}. \end{equation*}
We can use the vector addition of components to obtain the components of \(\vec v_{FG} \text{.}\)
\begin{align*} \vec v_{FG} \amp = \vec v_{FS} + \vec v_{SG}\\ \amp = (0, 4 \text{ m/s}) + (3 \text{ m/s}, 0)\\ \amp = (3 \text{ m/s}, 4 \text{ m/s}) \end{align*}
From this we can find the magnitude and angle \(\theta \text{.}\)
\begin{align*} \amp \text{Magnitude } = \sqrt{3^2 + 4^2} = 5\text{ m/s}.\\ \amp \theta = \tan^{-1} \dfrac{4}{3} = 53.1^{\circ} \end{align*}
Since the vector \((3 \text{ m/s}, 4 \text{ m/s}) \) is in the first qudrant, the angle we foound is the counterclockwise angle from the \(+x\) axis.
61. Crossing a River.
In order for you to cross a river exactly on the opposite side from one shore, you have to point the boat slightly up stream. This happens because your velocity with respect to shore is different from your velocity with respect to the river.
Let \(\vec v_{BS} \) be the velocity of the boat (B) with respect to the shore (S), \(\vec v_{BR} \) be the velocity of the boat (B) with respect to the river (R), and \(\vec v_{RS} \) be the velocity of the river stream (R) with respect to the shore (S). These vectors form a triangle as shown in the figure below. Notice that vectors \(\vec v_{BR} \) and \(\vec v_{RS} \) must add up to the vector \(\vec v_{BS} \text{.}\)
\begin{equation} \vec v_{BS} = \vec v_{BR} + \vec v_{RS}.\tag{3.38} \end{equation}
Now, the question. In order to cross the river directly on the other side, suppose you need to row the boat at speed \(5\text{ m/s} \) at \(\theta=30^{\circ}\) to directly across direction, which is the velocity of the boat with respect to the river. (a) What is the speed of the river? (b) If the river is \(100\text{ m}\) wide, how long would it take to cross the rivew?
Hint.
Express velocities in coordinate form and use Eq. (3.38).
Answer.
(a) \(2.5\text{ m/s}\text{,}\) (b) \(23.1\text{ s}\text{.}\)
Solution 1. a
Let’s use simpler notation in our calculations. Let \(v \) denote the speed of the river with respect to the shore. Let \(u\) be the speed of the boat with respect to the shore. Let \(x\) axis be in the direction of the river flow and \(y\) axis directly across. Then, Eq. (3.38), written using components form of the vectors is (suppressing the units):
\begin{equation*} (0, u) = (-5\sin 30^{\circ}, 5\cos 30^{\circ}) + (v, 0). \end{equation*}
This gives us two equations, one along the \(x \) axis and the other along the \(y \) axis.
\begin{gather*} 0 = -5\sin 30^{\circ} + v \\ u = 5\cos 30^{\circ} + 0 \end{gather*}
This gives \(u = 4.33\text{ m/s} \) and \(v = 2.5 \text{ m/s}\text{.}\) We will use \(u \) in part (b). The river is flowing at speed \(v = 2.5\text{ m/s} \text{.}\)
Solution 2. b
The boat moves at speed \(u = 4.33 \) m/s across the river which is \(d = 100\text{ m} \text{.}\) Therefore, it will take
\begin{equation*} t = \dfrac{d}{u} = \dfrac{100\text{ m}}{4.33 \text{ m/s}} = 23.1\text{ s}. \end{equation*}
62. Sum and Difference of a Time-dependent Vector and a Constant Vector.
Two vectors \(\vec A\) and \(\vec B\) are defined as \(\vec A=a\hat i\) and \(\vec B = a\left(\cos\,\omega t\,\hat i + \sin\,\omega t\,\hat j \right)\text{,}\) where \(a\) is a constant and \(\omega = \pi/6\text{ rad s}^{-1}\text{.}\)
If \(\left| \vec A + \vec B\right| = \sqrt{3} \left| \vec A - \vec B\right|\) at time \(t=\tau\) for the first time, find then value of \(\tau\) in seconds. (Adpated from Indian JEE Advanced, 2018)
Hint.
Use definition of square of amplitude of a vector.
Answer.
\(2.0\text{ sec}\text{.}\)
Solution.
This question can be answered by performing the algebra on the given condition.
\begin{align*} \amp \vec A = a\hat i,\ \ \vec B = a\left(\cos\,\omega t\,\hat i + \sin\,\omega t\,\hat j \right)\\ \amp \vec A + \vec B= (a + a \cos\,\omega t)\,\hat i + a \sin\,\omega t\,\hat j \\ \amp \vec A - \vec B= (a - a \cos\,\omega t)\,\hat i - a \sin\,\omega t\,\hat j \end{align*}
Therefore, square of \(\left| \vec A + \vec B\right| = \sqrt{3} \left| \vec A - \vec B\right|\) at \(t=\tau\) becomes
\begin{equation*} (a + a \cos\,\omega \tau)^2 + a^2 \sin^2\omega \tau = (\sqrt{3})^2\left[ (a - a \cos\,\omega \tau)^2 + a^2 \sin^2\omega \tau\right]. \end{equation*}
We can cancel out \(a^2\) from every term, expand \((1+\cos x)^2\) and use \(\sin^2 x + \cos^2 x = 1\text{,}\) where \(x=\omega \tau\text{.}\)
\begin{equation*} 1 + \cos\,\omega\tau = 3 ( 1 - \cos\,\omega\tau). \end{equation*}
This yields
\begin{equation*} \cos\,\omega\tau =\frac{1}{2}. \end{equation*}
Since \(\cos^{-1}\left(\frac{1}{2} \right) = \frac{\pi}{3}\text{ rad}\text{,}\) we have
\begin{align*} \tau \amp = \frac{6}{\pi}\times \frac{\pi}{3}= 2.0\text{ sec}. \end{align*}
63. Angle Between the Sum and Difference of Two Vectors of Equal Magnitude.
Prove that, if the magnitude of the two vectors \(\vec A\) and \(\vec B\) are equal, then \(\vec A+\vec B\) and \(\vec A-\vec B\) are perpendicular to each other.
Solution.
We are given that \(|\vec A| = |\vec B|\text{.}\) We will show that the dot product of \(\vec A+\vec B\) and \(\vec A-\vec B\) is zero by an explicit calculation. We make use of the fact that the dot product is commutative, that is the order of the vectors does not matter when taking the dot product, which would not be the case for the cross product. That is \(\vec A \cdot \vec B = \vec B \cdot \vec A\text{.}\) Now,
\begin{align*} \amp (\vec A+\vec B)\cdot (\vec A-\vec B)\\ \amp \ \ \ = \vec A \cdot \vec A - \vec A \cdot \vec B + \vec B \cdot \vec A - \vec B \cdot \vec B\\ \amp \ \ \ = |\vec A|^2 - |\vec B|^2 = 0. \end{align*}
Therefore, vector \(\vec A + \vec B\) must be perpendicular to the vector \(\vec A - \vec B\text{.}\)
64. Angle Between Vectors Whose Sum and Difference have Equal Magnitude.
Prove that, if \(|\vec A-\vec B| = |\vec A+\vec B|\text{,}\) then vector \(\vec A\) is perpendicular to vector \(\vec B\text{.}\)
Solution.
\(|\vec A-\vec B| = |\vec A+\vec B|\) means that \(|\vec A-\vec B|^2 = |\vec A+\vec B|^2\text{.}\) Now, writing out the two sides explicitly we have
\begin{equation*} |\vec A|^2 -2\vec A\cdot \vec B+ |\vec B|^2 = |\vec A|^2 +2\vec A\cdot \vec B+ |\vec B|^2, \end{equation*}
which gives
\begin{equation*} \vec A\cdot \vec B = 0, \end{equation*}
which proves that the two vectors are perpendicular to each other.
65. Two Vectors Having Same Dot Product with a Third Vector.
Suppose \(\vec A\cdot \vec B = \vec A\cdot \vec C\text{.}\) Is \(\vec B = \vec C\text{?}\) Why or why not? Give a graphical interpretation of the given statement also.
Solution.
Let us bring the two terms on the same side and write the given condition as
\begin{equation*} \vec A \cdot (\vec B - \vec C) = 0. \end{equation*}
This says that \(\vec A\) is perpendicular to whatever the vector \((\vec B - \vec C)\) happens to be. It is not necessary that \((\vec B - \vec C)\) be a null vector. Thus, \(\vec A\cdot \vec B = \vec A\cdot \vec C\) does not mean that \(\vec B = \vec C\text{.}\)
Graphically, take two arbitrary vectors \(\vec B\) and \(\vec C\) in space and draw vector \(\vec A\) perpendicular to the plane of vectors \(\vec B\) and \(\vec C\text{.}\) This situation will satisfy the given condition.
Figure 3.103.
66. Two Vectors Having Same Cross Product with a Third Vector.
Suppose \(\vec A\times \vec B = \vec A\times \vec C\text{.}\) Is \(\vec B = \vec C\text{?}\) Why or why not? What is the most we can say about \(\vec B\) and \(\vec C\text{?}\) Give a graphical interpretation of the given statement also.
Solution.
Let us bring the two terms on the same side and write the given condition as
\begin{equation*} \vec A \times (\vec B - \vec C) = 0. \end{equation*}
This says that \(\vec A\) is parallel to whatever the vector \((\vec B - \vec C)\) happens to be. It is not necessary that \((\vec B - \vec C)\) be a null vector. Thus, \(\vec A\times \vec B = \vec A\times \vec C\) does not mean that \(\vec B = \vec C\text{.}\)
Graphically, take two arbitrary vectors \(\vec B\) and \(\vec C\) in space and draw vector \(\vec A\) parallel or anti-parallel to the difference vector \(\vec B -\vec C\text{.}\) This situation will satisfy the given condition for arbitrary vectors \(\vec B\) and \(\vec C\text{.}\)
Figure 3.104.
67. Two Vectors Having Same Dot and Cross Products with a Third Vector.
Suppose \(\vec A\cdot \vec B = \vec A\cdot \vec C\) \emph{and} \(\vec A\times \vec B = \vec A\times \vec C\text{.}\) Is \(\vec B = \vec C\text{?}\) Why or why not?
Solution.
As we have seen above that \(\vec A\cdot \vec B = \vec A\cdot \vec C\) means that the vector \(\vec A\) is perpendicular to \((\vec B - \vec C)\) and \(\vec A\times \vec B = \vec A\times \vec C\) means that the vector \(\vec A\) is parallel to \((\vec B - \vec C)\text{.}\) Now, two vectors cannot be both parallel and perpendicular to each other unless one of them is a null vector. Therefore, if \(\vec A\) is not a null vector, then
\begin{equation*} \vec B - \vec C = 0\ \ \Longrightarrow \ \ \vec B = \vec C. \end{equation*}
68. Decomposing a Vector into Components Parallel and Perpendicular to a Unit Vector.
Often, we are interested in how much of a vector is along some given unit vector and along some direction perpendicular to that unit vector. Let \(\hat u\) be a given unit vector. Show the following relation holds for an arbitrary vector \(\vec A\text{.}\)
\begin{equation*} \vec A = \vec A_\parallel + \vec A_\perp, \end{equation*}
where the parallel and perpendicular components of \(\vec A\) are
\begin{align*} \amp \vec A_\parallel = (\hat u \cdot \vec A)\, \hat u,\ \ \ \vec A_\perp = (\hat u \times \vec A)\times \hat u. \end{align*}
Solution.
Let’s look at the plane formed by non-zero vectors \(\vec A\) and \(\hat u\text{.}\) Let \(\hat n\) be a vector normal to \(\hat u\text{.}\) If this plane was \(xy\)-plane and you took positive \(x\)-axis towards \(\hat u\text{,}\) then you could choose \(y\)-axis towards \(\hat n\text{.}\)
From the projection of \(\vec A\) on the unit vectors \(\hat u\) and \(\hat n\text{,}\) we get
\begin{equation} \vec A = a\, \hat u + b\, \hat n.\tag{3.39} \end{equation}
The unit vectors have the following dot and cross products.
\begin{align*} \amp \hat u \cdot \hat u = 1,\ \ \hat n \cdot \hat n = 1, \hat u \cdot \hat n = 0,\\ \amp \hat u \times \hat u = 0,\ \ \hat n \times \hat n = 0, \hat u \times \hat n = \hat w,\\ \amp \hat n \times \hat w = \hat u,\ \ \hat w \times \hat u = \hat n \end{align*}
where \(\hat w\) is a unit vector that is perpendicular to the plane of \(\hat u\) and \(\vec A\text{.}\)
\begin{equation*} \vec A \cdot \hat w = 0. \end{equation*}
Now, we take dot product with \(\hat u\) of Eq. (3.39) to get
\begin{equation*} \hat u \cdot \vec A = a\, (\hat u \cdot \hat u) + b\, (\hat u \cdot \hat n) = a. \end{equation*}
When we take cross product with \(\hat u\text{,}\) we get
\begin{equation*} \hat u \times \vec A = a\, (\hat u \times \hat u) + b\, (\hat u \times \hat n) = b \hat w. \end{equation*}
We can get rid of \(\hat w\) if we take another cross product with \(\hat u\text{.}\)
\begin{equation*} (\hat u \times \vec A)\times \hat u = b \hat w \hat u = b \hat n. \end{equation*}
Hence, we have
\begin{equation*} \vec A = (\hat u \times \vec A )\, \hat u + (\hat u \times \vec A)\times \hat u. \end{equation*}
69. Practice with a Friend: Vector Identities.
Prove the following identities for two arbitrary vectors \(\vec A\) and \(\vec B\text{.}\)
\begin{align} \amp \vec A \cdot \vec B = \vec B \cdot \vec A\tag{3.40}\\ \amp \vec A \times \vec B = - \vec B \times \vec A\tag{3.41} \end{align}
70. Practice with a Friend: Vector Identities.
Prove the following identitiy for three arbitrary vectors \(\vec A\text{,}\) \(\vec B\text{,}\) and \(\vec C\text{,}\) called the cab-bac equation.
\begin{equation*} \vec A \times (\vec B \times \vec C)= (\vec C\cdot \vec A) \vec B - (\vec B\cdot \vec A)\vec C \end{equation*}
Maybe you want to show that \(x\) component of each side comes out the same.
71. Practice with a Friend: Prove a Plane Geometry Result Using Vectors..
If the diagonals of a parallelogram are equal, then the sides must be perpendicular to each other.
Hint.
Place two vectors \(\vec A\) and \(\vec A\) on two adjecent sides. Then, notice that the diagonals are \(\vec A + \vec B\) and \(\vec A - \vec B\text{.}\) Use dot product between them to prove the result.
PrevTopNext
Found typo?