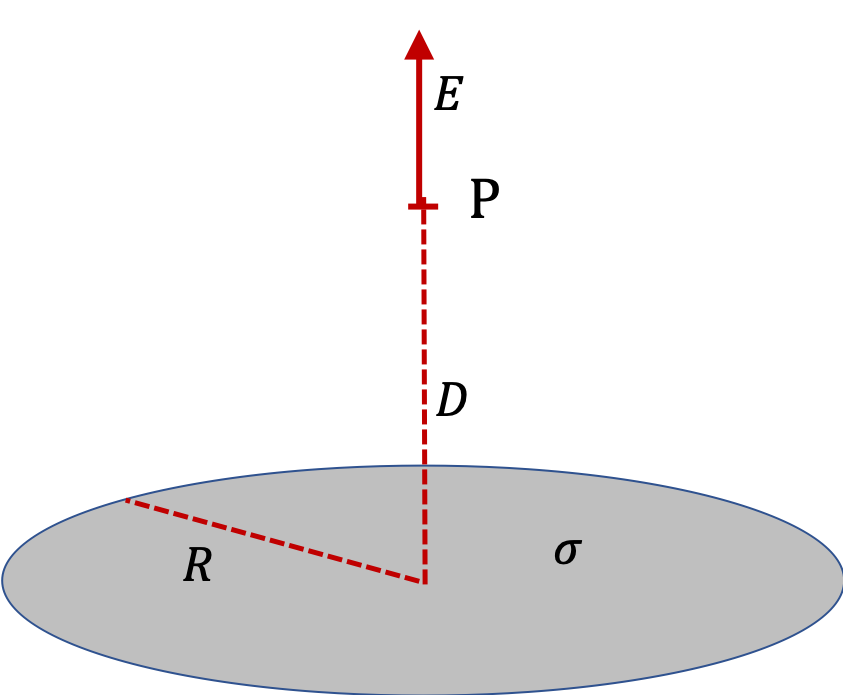
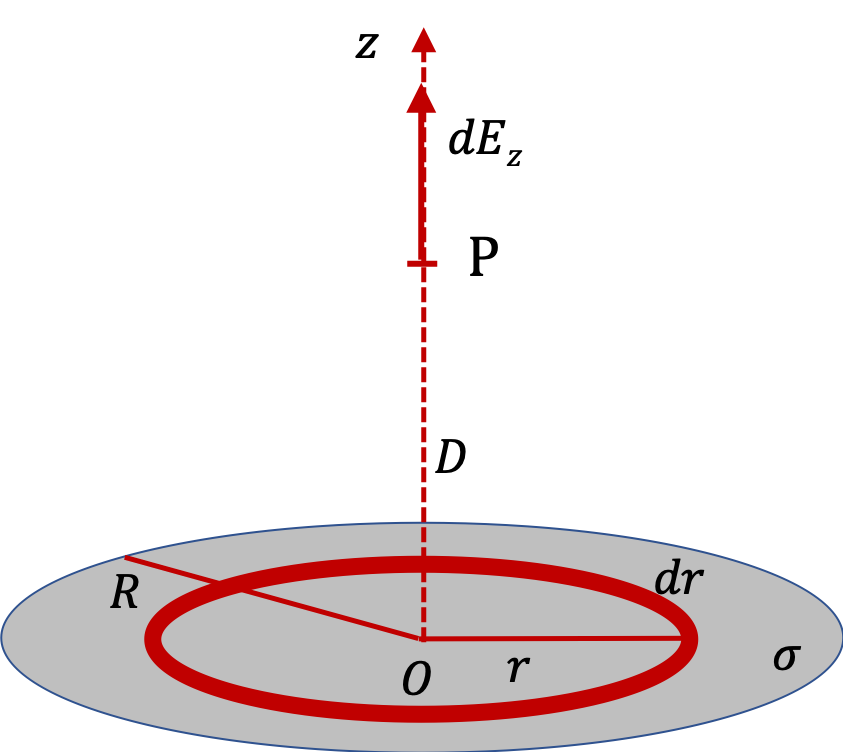
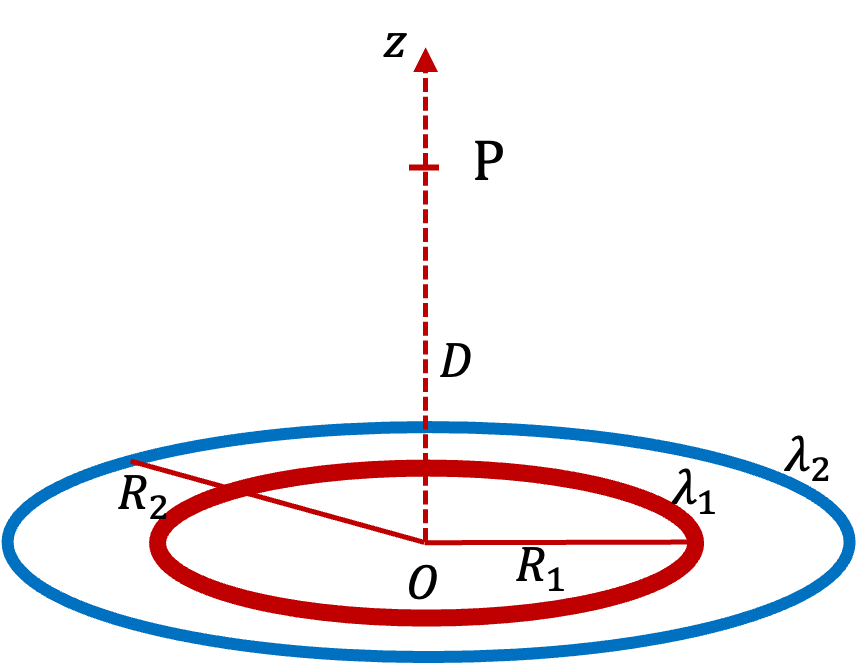
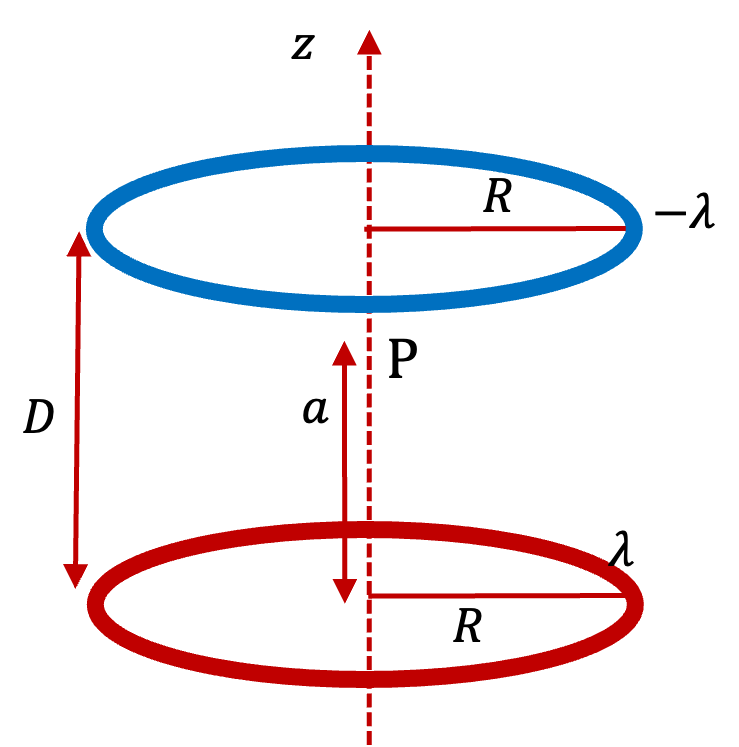
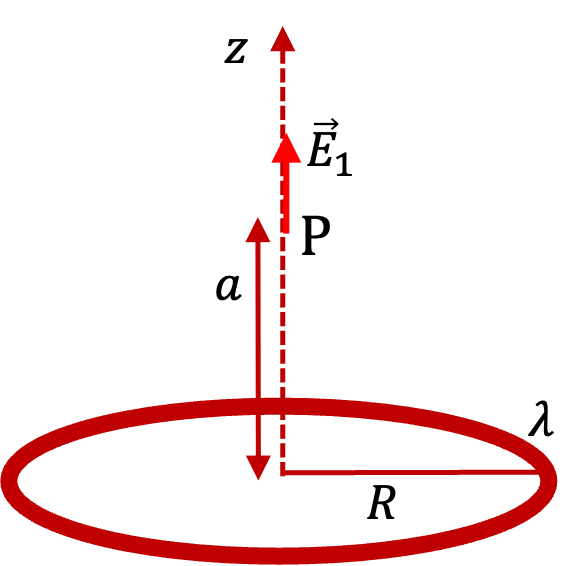
Example 29.36. Electric Field of a Uniformly Charged Thin Rod.
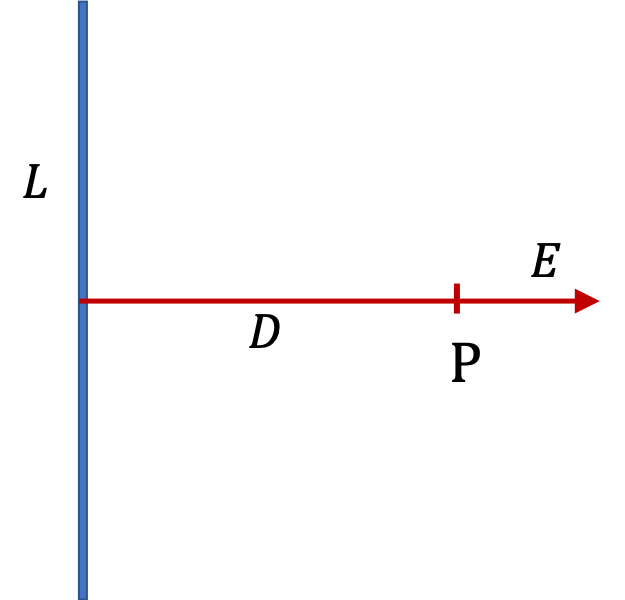
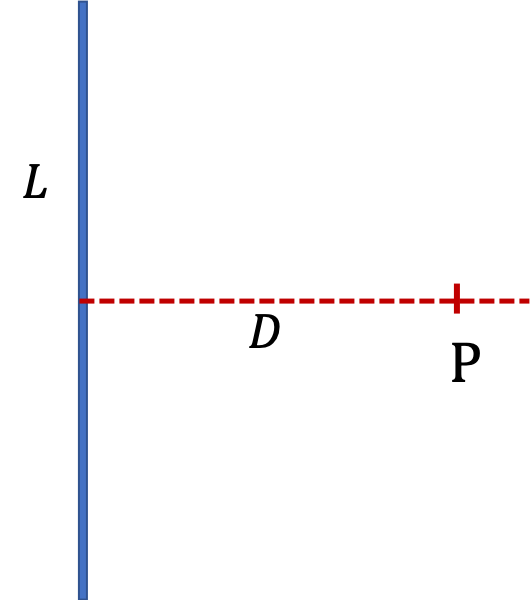
Suppose we have a uniformly charged rod of length \(L\) with line charge density \(\lambda\) and we want to find field at P in Figure 29.37. The electric field is given in Eq. (29.22).
\begin{equation*}
E = k\dfrac{ 2|q| }{ D \sqrt{ L^2 + 4D^2} },
\end{equation*}
Now, we will like to derive this result from the fundametal formula for electric field of a point charge.
General Strategy:
When we deal with a continuous charges, it is helpful to start with pieces of the body, and use point charge formula. Whenever possible, it usually simplifies calculation if you make use of the symmetry. In the present question, since the field point is in the plane that divides the rod in half, there is a symmetry between the upper half and lower half.
Derivation:
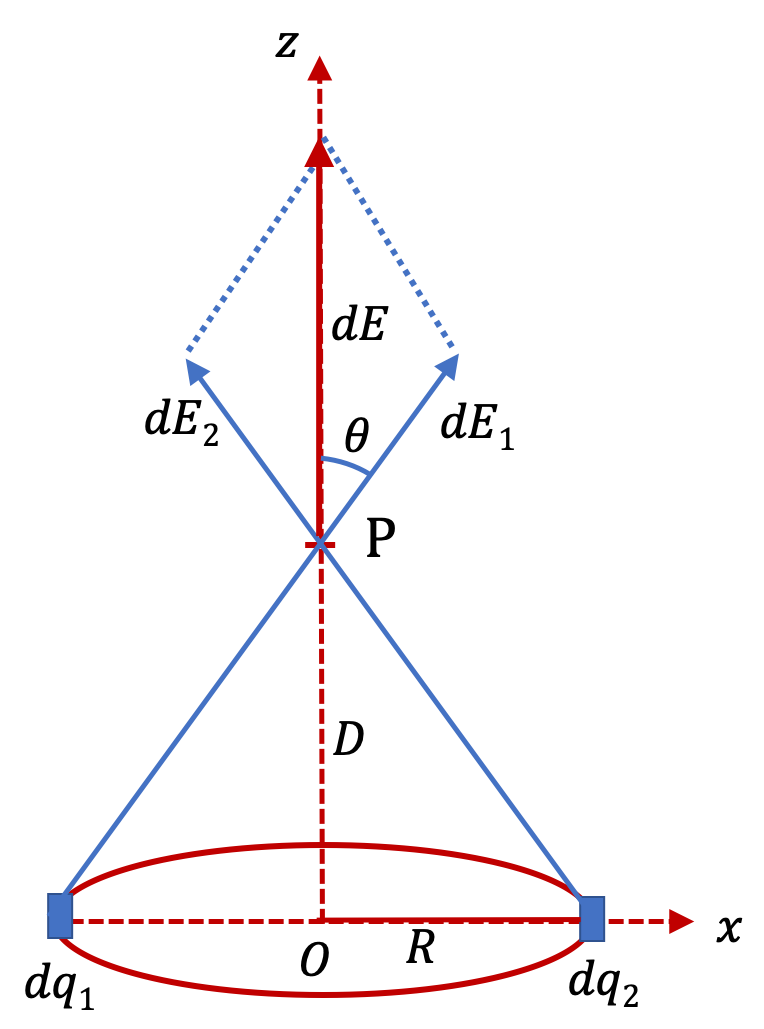
To exploit symmetry in the situation, we will look at electric fields from two small parts of the rod that are symmetrucally placed shown as \(dq_1\) and \(dq_2\) in Figure 29.38. Note that the symmetry leads to the cancellation of \(y\) component. Hence, we just need to work out \(E_x\text{.}\) furthermore, we can find \(E_x\) from one half of the rod and double that.
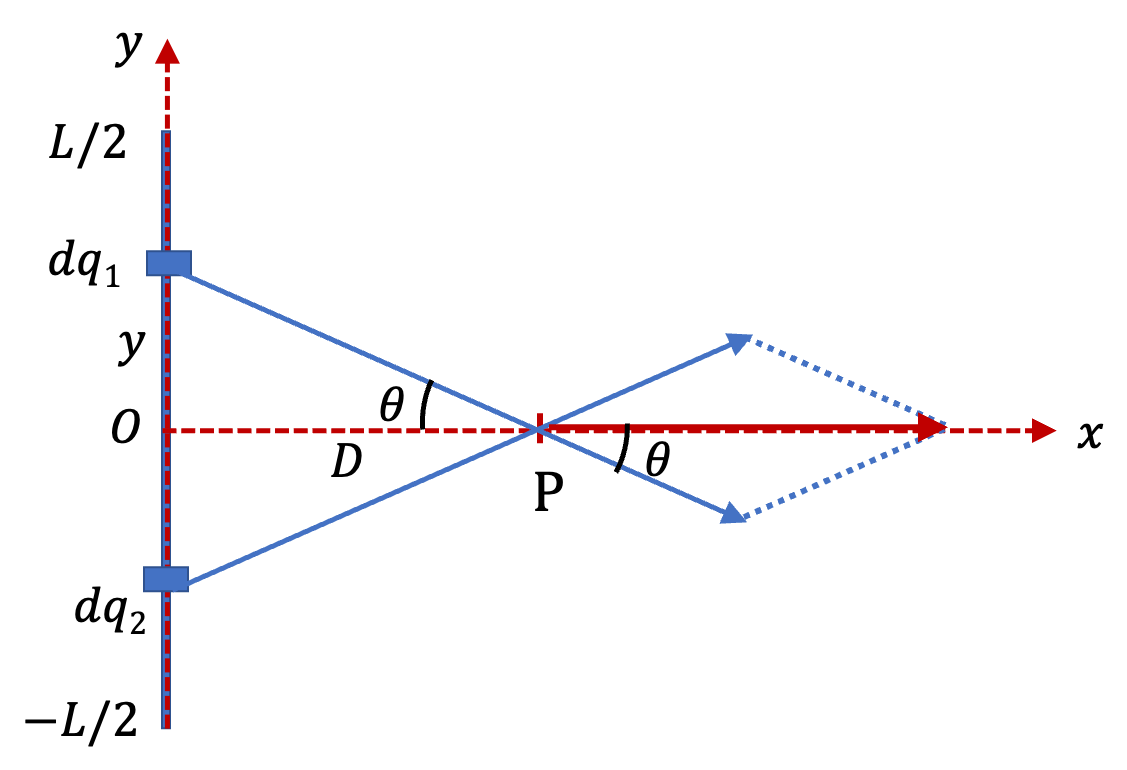
From element of the rod between \(y\) and \(y+dy\text{,}\) shown in the upper part of the rod in Figure 29.39 the \(x\)-component of the electric field, to be written informally in infinitesimal notation of \(dE_x\text{,}\) is
\begin{align*}
dE_x \amp = k \dfrac{\lambda\, dy}{ D^2 + y^2 }\, \cos\theta\\
\amp = k \dfrac{\lambda\, dy}{ D^2 + y^2 }\, \dfrac{D}{ \sqrt{D^2 + y^2} }
\end{align*}
To get the net electric field from the rod we will integrate the right side from \(y=0\) to \(y=L/2\) and multiply the result by 2 to take into account the contributions of the lower half.
\begin{align*}
E_x \amp = 2\times k\,\lambda\, D \int_0^{L/2} \dfrac{dy}{ \left( D^2 + y^2 \right)^{3/2} }.
\end{align*}
I will use Wolfram Alpha to find the integral
3
\begin{equation*}
\int \dfrac{dy}{ \left( D^2 + y^2 \right)^{3/2} } = \dfrac{y}{D^2\sqrt{y^2 + D^2}} + C.
\end{equation*}
Therefore, we will get following answer for our problem.
\begin{align*}
E_x \amp = 2\times k\,\lambda\, \dfrac{L/2}{D\sqrt{(L/2)^2 + D^2}}.
\end{align*}
Now, we see that \(\lambda L\) is the total charge on the rod. Let us denote this by \(q\text{.}\)
\begin{equation}
E_x = k\, \dfrac{q}{D\sqrt{(L/2)^2 + D^2}}.\tag{29.23}
\end{equation}
Therefore, the magnitude is
\begin{equation*}
E = k\, \dfrac{|q|}{D\sqrt{(L/2)^2 + D^2}} = k\, \dfrac{2|q|}{D\sqrt{L^2 + 4\:D^2}},
\end{equation*}
the direction towards \(+x\) if \(q\) positive and \(-x\) if \(q\) negative.
Notice that if P is very far away, our rod would look like a point charge, therefore, our answer should become same as that of point charge. We can see this expectation emerge when we apply \(D\gt\gt L\) limit our result in Eq. (29.23) by just dropping \((L/2)^2\) compared to \(D^2\text{.}\)
\begin{equation*}
E_x = k\, \dfrac{q}{D^2}\text{, if } D\gt\gt L.
\end{equation*}