Example 26.8. (Calculus) Entropy Change in Equilibration of a Two Compartment System.
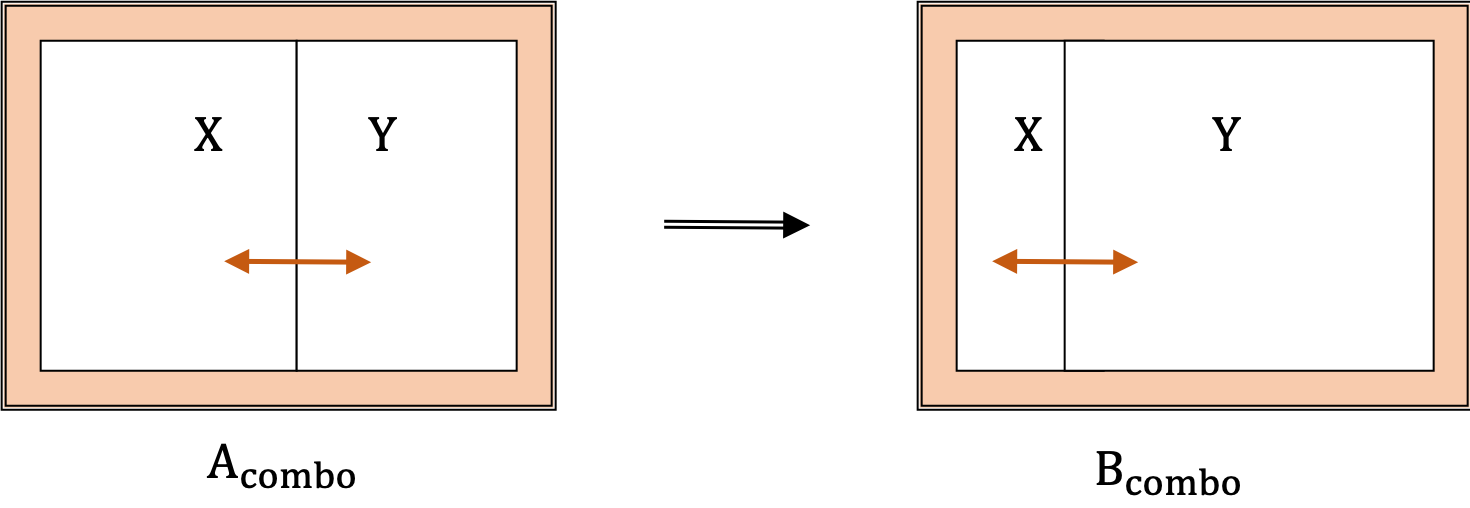
A nonconducting cylinder of total volume \(2\) L closed at both ends is divided into two parts by a diathermal frictionless circular wall as shown in Figure 26.9.

Initially the piston is clamped in the middle with the Nitrogen gas, assumed to be an ideal gas of \(C_V=\frac{5}{2}R\text{,}\) at different temperatures and pressures on the two side. The initial pressure and temperatures on the left and right sides are (\(3\) atm, \(330\)K) and (\(2\) atm, \(250\)K) respectively.
(a) Find the temperature and pressure of the final state when the two sides are in thermal and mechanical equilibrium. (b) Find the net change in the entropy of the gas.
Answer.
(a) \(2.51\ \textrm{atm}\text{,}\) \(V_1 = 1.064\ \textrm{L}\text{,}\) \(V_2 = 0.936\ \textrm{L}. \) (b) see the solution.
Solution 1. a
From the given data on the left and right chambers in the ideal gas law for each we obtain
\begin{align*}
\amp n_1 = \frac{p_1 (V_0/2)}{RT_1} = 0.111\ \textrm{mol}.\\
\amp n_1 = \frac{p_2 (V_0/2)}{RT_2} = 0.0976\ \textrm{mol}.
\end{align*}
Now, we find the common pressure \(p\) and temperature \(T\) values in the two chambers in the final state. To find the temperature we note that total energy of the two systems will not change since although the gas on the sides interact with each other, the two together are isolated from other systems.
\begin{equation*}
\Delta U = \Delta U_1 + \Delta U_2 = 0.
\end{equation*}
The change in the internal energies of the two sides separately will be
\begin{align*}
\amp \Delta U_1 = n_1 C_V (T - T_1).\\
\amp \Delta U_2 = n_2 C_V (T - T_2).
\end{align*}
Therefore,
\begin{equation*}
T = \frac{ n_1 T_1 + n_2 T_2}{ n_1 + n_2 } = \frac{ 0.111 \times 330+ 0.0976\times 250 }{ 0.111 + 0.0976 } = 293\ \textrm{K}.
\end{equation*}
Let \(V_1\) and \(V_2\) be the volumes on the left and right sides at equilibrium. Let us denote the total volume by \(V_0\text{.}\) Then, we have
\begin{equation}
V_1 + V_2 = V_0. \tag{26.17}
\end{equation}
The volumes on the two sides are also given by the ideal gas laws on the two sides.
\begin{align*}
\amp V_1 = n_1 \frac{R T}{p} \equiv n_1 x.\\
\amp V_2 = n_2 \frac{R T}{p} = n_2 x.
\end{align*}
Put these in Eq. (26.17) to obtain
\begin{equation*}
V_1 = 1.064\ \textrm{L},\ \ V_2 = 0.936\ \textrm{L}.
\end{equation*}
Now, applying the ideal gas law on either of the chamber in the final state gives
\begin{equation*}
p = \frac{n_1RT}{V_1} = \frac{0.111\ \textrm{mol} \times 0.082\ \textrm{L.atm/mol.K}\times 293}{1.064\ \textrm{L}} = 2.51\ \textrm{atm}.
\end{equation*}
Solution 2. b
To compute the entropy change, we envision reversible steps that lead to the same change in state but where the computation of entropy changes are easier to compute. Figure 26.10 gives one set of possible easy-to-compute processes in the
pV
-planes of the gases in the two compartments.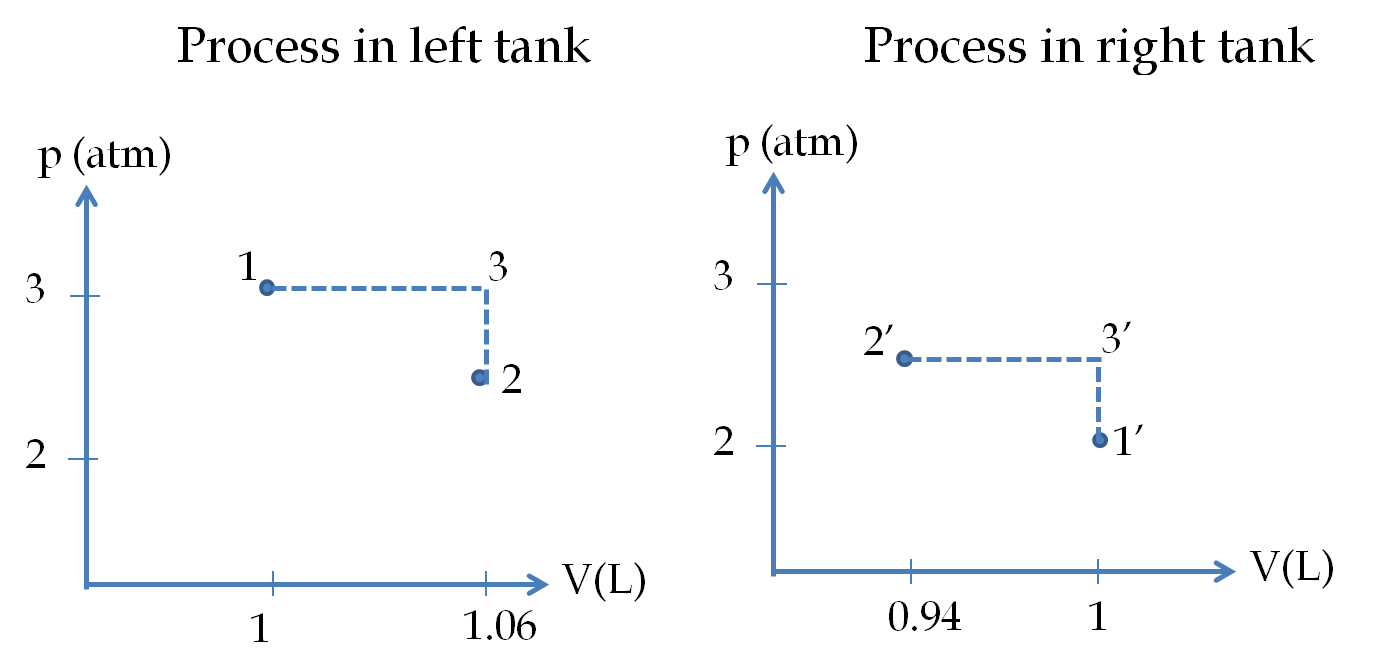
For a constant-pressure step,
\begin{equation*}
\Delta S = n\, C_P\,\ln\dfrac{T_2}{T_1} = n\, C_P\,\ln\dfrac{V_2}{V_1},
\end{equation*}
and for a constant-pressure step,
\begin{equation*}
\Delta S = n\, C_V\,\ln\dfrac{T_2}{T_1} = n\, C_V\,\ln\dfrac{V_2}{V_1},
\end{equation*}
with
\begin{equation*}
C_P = C_V + R = \dfrac{7}{2}R.
\end{equation*}
For the case of gas in the left chamber we have
\begin{equation*}
\Delta S_{12} = \Delta S_{13} + \Delta S_{32},
\end{equation*}
with
\begin{equation*}
\Delta S_{13} = n_L \dfrac{7}{2}R \ln\dfrac{V_3}{V_1},
\end{equation*}
and
\begin{equation*}
\Delta S_{23} = n_L \dfrac{5}{2}R \ln\dfrac{V_2}{V_3}.
\end{equation*}
You can work out similar exprssions for the gas in the right tank. Adding the change in left tank and the right tank will give the ne change.