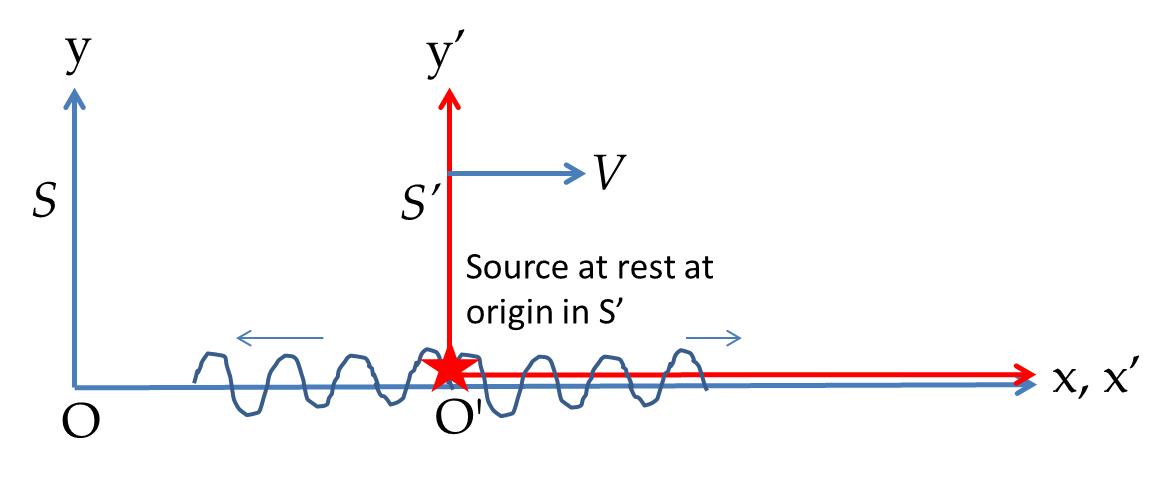
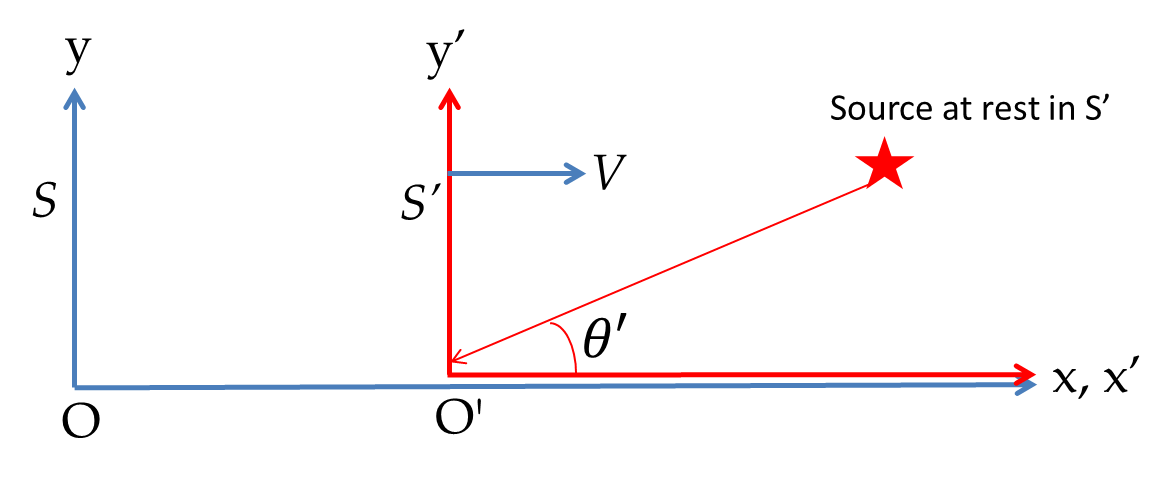
In the last subsection we studied the relativistic Doppler effect for the relative motion along the line joining the source and the observer. Now, we suppose the source of the wave is in the \(xy\)-plane and is at rest in the \(\text{S}^{\:\prime}\) frame at an angle \(\theta'\) in the first quadrant from the origin and counterclockwise from the \(x'\)-axis.
The propagation vector for the ray from the source will be
\begin{equation}
\vec k = \dfrac{2\pi}{\lambda_0}\: \left(-\cos\theta'\:\hat i -\sin\theta'\:\hat j \right),\tag{49.58}
\end{equation}
where \(k\) is the wavenumber, and \(\hat i\) and \(\hat j\) are unit vectors towards the positive \(x'\) and \(y'\) axes respectively. The wavenumber \(k\) is related to the wavelength \(\lambda\) by \(k = 2\pi/\lambda\text{.}\) Using a general form for oscillating part of plane waves, \(\sim \cos(\vec k\cdot \vec r - 2\pi f t)\text{,}\) the wave function for this wave will be
\begin{equation}
\psi^{\prime} (x',t') = \psi_0^{\prime}\cos\left[ \dfrac{2\pi}{\lambda_0} (-x'\cos\theta' - y'\sin\theta') - 2\pi f_0 t'\right]. \tag{49.59}
\end{equation}
Now, we express
\(x'\text{,}\) \(y'\text{,}\) and
\(t'\) in Eq.
(49.51) in terms of
\(x\text{,}\) \(y\text{,}\) and
\(t\) using the Lorentz transformations, and collect terms in the argument of cosine as a term multiplying
\(x\text{,}\) a term multiplying
\(y\text{,}\) and another term multiplying
\(t\text{.}\) We also use
\(\lambda_0 f_0 = c\) to simplify.
\begin{align*}
\psi^{\prime} (x,t) = \psi_0^{\prime} \amp \cos\left[ 2\pi\gamma \dfrac{1}{\lambda_0}\left( -\cos\theta' + \dfrac{V }{c} \right)\: x \right.\\
\amp - \left. 2\pi\dfrac{\sin\theta'}{\lambda_0}\: y - 2\pi\gamma f_0\left(1 - \dfrac{V}{c}\: \cos\theta'\right)\: t\right].
\end{align*}
The detector/observer at the origin of the S frame will find this wave coming from the direction \(\theta\) and assign the following wave function.
\begin{equation}
\psi (x,t) = \psi_0 \cos\left[ \dfrac{2\pi}{\lambda} (x\cos\theta + y\sin\theta) - 2\pi f t\right]. \tag{49.60}
\end{equation}
Now, we equate the coefficients of \(x\text{,}\) \(y\text{,}\) and \(t\) in the argument of cosine in the last two equations to obtain
\begin{align}
\amp \dfrac{\cos\theta}{\lambda} = \gamma \dfrac{1}{\lambda_0}\left( -\cos\theta' + \dfrac{V }{c} \right) \tag{49.61}\\
\amp \dfrac{\sin\theta}{\lambda} = \dfrac{\sin\theta'}{\lambda_0}\tag{49.62}\\
\amp f = \gamma\left(1 - \dfrac{V}{c}\: \cos\theta'\right)\: f_0 \tag{49.63}
\end{align}
We can eliminate
\(\cos\theta'\) in Eq.
(49.63) in favor of
\(\cos\theta\text{.}\) This gives the Doppler shift from a source whose direction is
\(\theta\) in the frame of the observer while the source is moving at velocity in the direction of
\(\theta = 0\text{,}\) i.e., the positive
\(x\)-axis.
\begin{equation}
f = \left[\frac{1-(V/c)\cos\theta}{\sqrt{1-V^2/c^2}}\right]\ f_0. \tag{49.64}
\end{equation}
There is a Doppler effect even when the source is moving in the perpendicular direction. To see that we set \(\theta = 90^{\circ}\) in this equation gives the Doppler shift of an object that is towards the \(y\)-axis and moving towards the positive \(x\)-axis. This effect is called the Transverse Doppler Effect.
\begin{equation}
f = f_0\:\sqrt{1-V^2/c^2}. \tag{49.65}
\end{equation}
The transverse Doppler effect is much weaker than the longitudinal Doppler effect obtained in Eq.
(49.56). Let us expand Eqs.
(49.56) and
(49.65) in powers of
\(V/c\text{.}\) Let us designate the longitudinal Doppler by
\(f_{\parallel}\) and the transverse Doppler by
\(f_{\perp}\text{.}\)
\begin{align}
f_{\parallel} \amp = f_0 \left[\left(1 - \dfrac{V}{c} \right) \dfrac{1}{\sqrt{1-V^2/c^2}} \right]\notag\\
\amp = f_0\: \left(1 - V/c + V^2/2c^2 +\cdots\right) \tag{49.66}\\
f_{\perp} \amp = f_0 \sqrt{1-V^2/c^2} = f_0\: \left(1 - V^2/2c^2 +\cdots\right) \tag{49.67}
\end{align}
Dividing Eqs.
(49.61) and
(49.61) gives us the following relation between the direction of the source in the two systems.
\begin{equation}
\tan\theta = \frac{\sin\theta'\: \sqrt{1-V^2/c^2}}{\cos\theta' - V/c}.\tag{49.68}
\end{equation}
This relation says light emitted at a direction \(\theta'\) in one frame will coming from the direction \(\theta\) in the other frame. The phenomenon is called the aberration of light. For instance, if the source is on the \(y'\) axis, the angle \(\theta' = 90^{\circ}\text{.}\) But the angle \(\theta\) in the S frame will be
\begin{equation}
\theta = - \tan^{-1}\left( \frac{\sqrt{1-V^2/c^2}}{V/c}\right)\approx - \tan^{-1}\left(\dfrac{c}{V} \right).\tag{49.69}
\end{equation}