Charged Particles in Electric Field

Section 29.7 Charged Particles in Electric Field

In many accelerator experiments, it is common practice to accelerate charged particles by placing the particle in an electric field. If you place a particle of charge \(q\) in electric field \(\vec E\text{,}\) the force on the particle will be given by

\begin{equation} \vec F_\text{on q} = q\:\vec E.\tag{29.28} \end{equation}

In this section we will work out examples of motion of particles when electric force is the only force on the particle. Later on, when we discuss magnetic force, we will look at another way we can change the motion of a particle based on its charge.

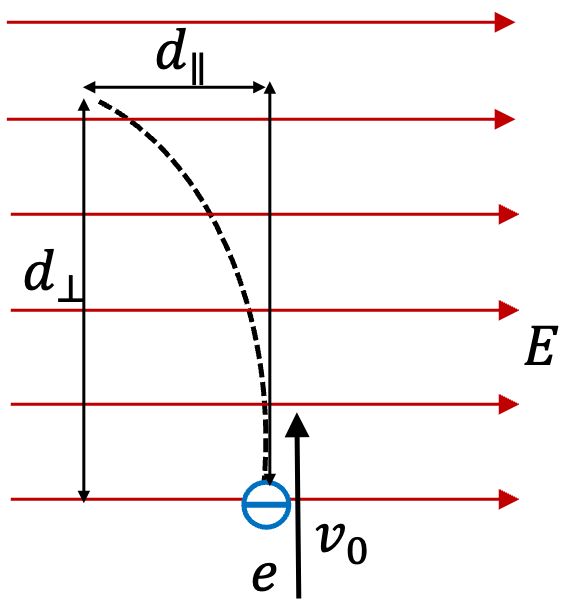
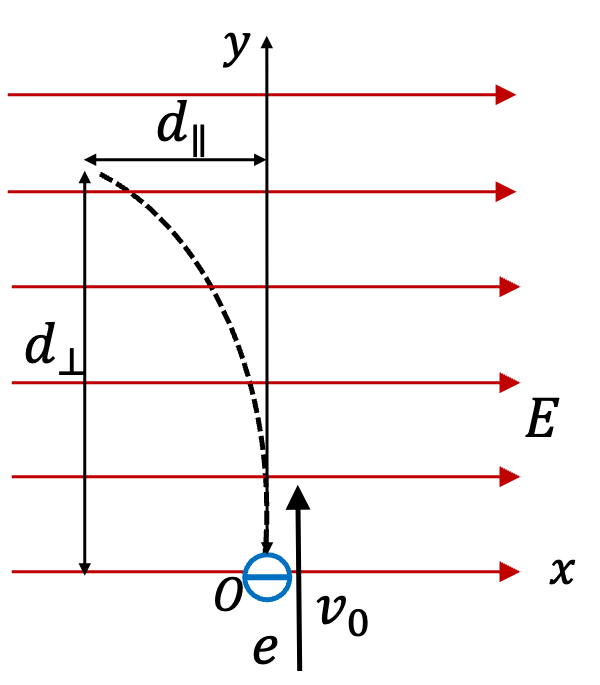
Example 29.55. Motion of an Electron with Initial Velocity Parallel to the Electric Field.

An electron with speed \(2.0\times 10^5\text{ m/s}\) enters a region of constant electric field of magnitude \(1000\text{ N/C}\) from a direction so that initial velocity is in the opposite to the direction as the electric field.

(a) What is the magnitude and direction of acceleration of the electron?

(b) What is the velocity of the electron after \(5.0\ \text{ ns}\text{?}\)

(c) What is the velocity of the electron after it has covered a distance of \(4.0\text{ mm}\) in the non-zero electric field region?

Answer.

(a) \(1.8\times 10^{14}\text{ m/s}^2\) opposite to direction of electric field, (b) \(1.1\times 10^6\text{ m/s}\) opposite to direction of electric field, (c) \(1.36 \times 10^{6} \text{ m/s}\) opposite to direction of electric field.

Solution 1. (a)

(a) Since electron is negatively charged, force on the electron will be in the opposite direction of the electric field. Let electric field direction be towards \(x\) axis. Then, we see that the acceleration will have only \(x\) component.

\begin{align*} a_x \amp = \frac{F_x}{m} = \frac{q E_x}{m} \\ \amp = \frac{-1.60\times 10^{-19}\text{ C}\times 1000\text{ N/C}}{9.1\times 10^{-31}\text{ kg} } = - 1.8\times 10^{14}\text{ m/s}^2 \end{align*}

Solution 2. (b)

(b) The initial velocity is pointed in the negative \(x\) axis. Therefore, we have

\begin{equation*} v_{ix} = -2.0\times 10^5\text{ m/s}. \end{equation*}

Since acceleration is constant, we will get

\begin{align*} v_{fx} \amp = v_{ix} + a_x t \\ \amp = -2.0\times 10^5\text{ m/s} - 1.8\times 10^{14}\text{ m/s}^2\times 5.0\times 10^{-9}\text{ s}\\ \amp = -2.0\times 10^5\text{ m/s} - 9\times 10^{5} \text{ m/s} = -1.1\times 10^6\text{ m/s}. \end{align*}

Solution 3. (c)

\begin{equation*} v_{fx} = - \sqrt{ v_{ix}^2 + 2 a_x \Delta x }, \end{equation*}

where I used the negative root since velocity is pointed towards negative \(x\) axis. Here, both \(a_x\) and \(\Delta x \) are negative. Now, using the given numbers we get

\begin{align*} v_{fx} \amp = - \sqrt{ (2.0\times 10^5)^2 + 2 \times 1.8\times 10^{14}\text{ m/s}^2 \times 5.0\times 10^{-3}\text{ m}} \\ \amp = - 1.36 \times 10^{6} \text{ m/s}. \end{align*}

Example 29.56. Motion of an Electron with Initial Velocity Perpendicular to the Electric Field.

An electron with speed \(v_0\) enters a region of constant electric field of magnitude \(E\) from a direction so that initial velocity is perpendicular to the direction of the electric field as shown in the figure.

Electron’s path is parabolic such that, for \(d_\perp\) in the forward direction, the electron moves a distance \(d_\parallel\) in the direction parallel to the electric field. Find \(d_\parallel\) in terms of \(d_\perp\text{.}\) Use symbol \(m_e\) for mass of electron and charge \(-e\) for its charge.

Answer.

\(d_\parallel = \frac{eE}{2m_ev_0^2} d_\perp^2\text{.}\)

Solution.

This is similar to projectile motion. Let us introduce \(x\) and \(y\) axes so we can work with component motions. With these axes, we have

\begin{align*} \amp v_{ix}=0,\ v_{iy}=v_0,\ x_i=0,\ y_i=0\\ \amp a_x = - eE/m_e,\ a_y=0,\ x_f=-d_\parallel,\ y_f=d_\perp. \end{align*}

Let \(t\) be the duration. Then, we have the following two equations for \(x\) and \(y\) motions.

\begin{align*} -\amp d_\parallel = 0 + \frac{1}{2}a_x t^2 = -\frac{eE}{2m_e} t^2.\\ \amp d_\perp = v_0 t. \end{align*}

Squaring the second equation and dividing the first gets rid of \(t\) and gives us the following relation.

\begin{equation*} d_\parallel = \frac{eE}{2m_ev_0^2} d_\perp^2. \end{equation*}