Section 51.2 Evidence for Matter Waves
According to de Broglie, electrons (and all matter) are fundamentally waves. As waves they should exhibit interference and diffraction phenomena. Soon after the suggestion by de Broglie, a laboratory accident in Davisson’s lab led to experiments that showed the wave-like behavior of electrons which was confirmed by another experiment by G. P. Thomson, the son of J. J. Thomson, the discoverer of electron in cathode rays. Since then, experiments have been done to demonstrate that other particles such as neutrons and also atoms have wave-like properties. We will study the two influential experiments done early on electrons, and a more modern experiment using individual electrons.
Subsection 51.2.1 The Davisson-Germer Experiment
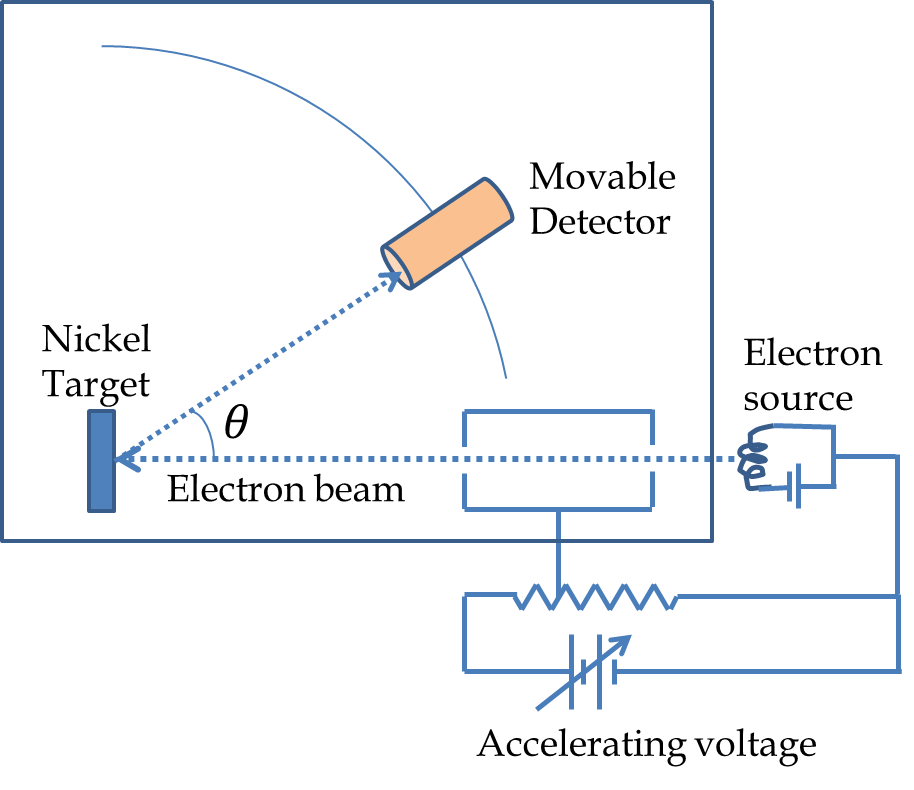
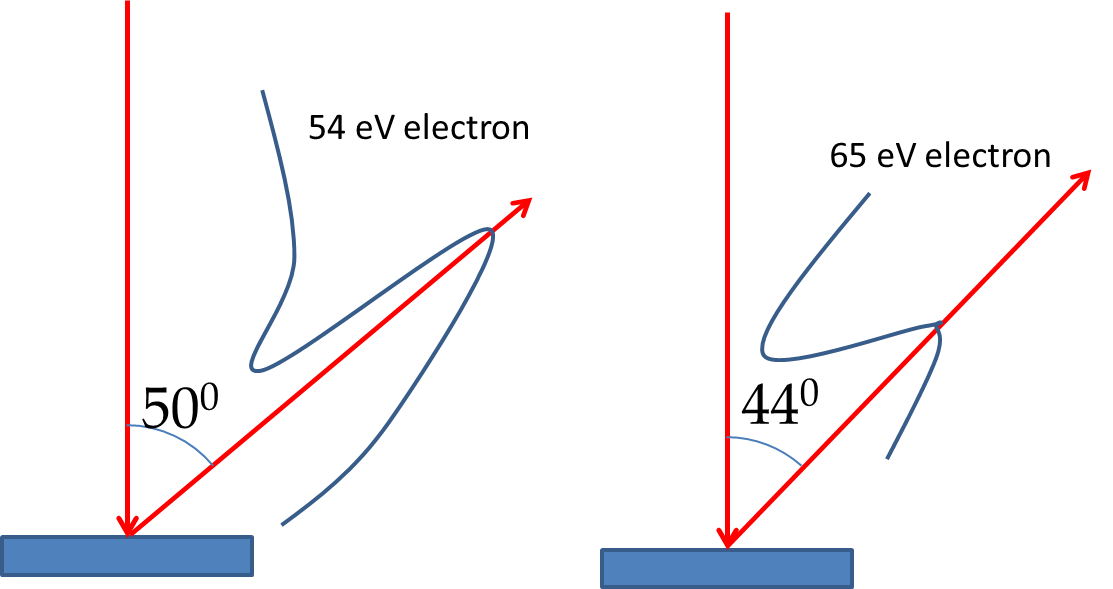
Figure 51.6 shows a schematic picture of the apparatus used by C. J. Davisson and L. H. Germer of Bell Labs, New York. In their experiment they placed a Nickel crystal in a vacuum chamber struck it with an electron beam. They measured the intensity of the scattered electrons at various angles. They were surprised to find that electron intensity varied with direction and the energy of the electrons as shown in the intensity profiles in Figure 51.6. For instance, they found that the intensity for a \(54\:\textrm{eV}\) electron was maximum at \(50^{\circ}\text{.}\) They interpreted their result in terms of electrons diffracting as waves according to the rules proposed by de Broglie similar to the Bragg diffraction of X-rays.
To obtain the Bragg diffraction condition for electrons incident on Nickel we refer to Figure 51.7. The Bragg law is written in terms of the glancing angle \(\theta\) with respect to the scattering planes as shown in the figure. The path difference between the two reflected beams gives the following condition for Bragg diffraction.
\begin{equation*}
2 d \sin\theta = n \lambda,
\end{equation*}
where \(d\) is the inter-plane spacing. We can write \(d\) in terms of the inter-atomic distance \(a\) in the Nickel crystal, which is
\begin{equation*}
a = 0.215\:\textrm{nm}.
\end{equation*}
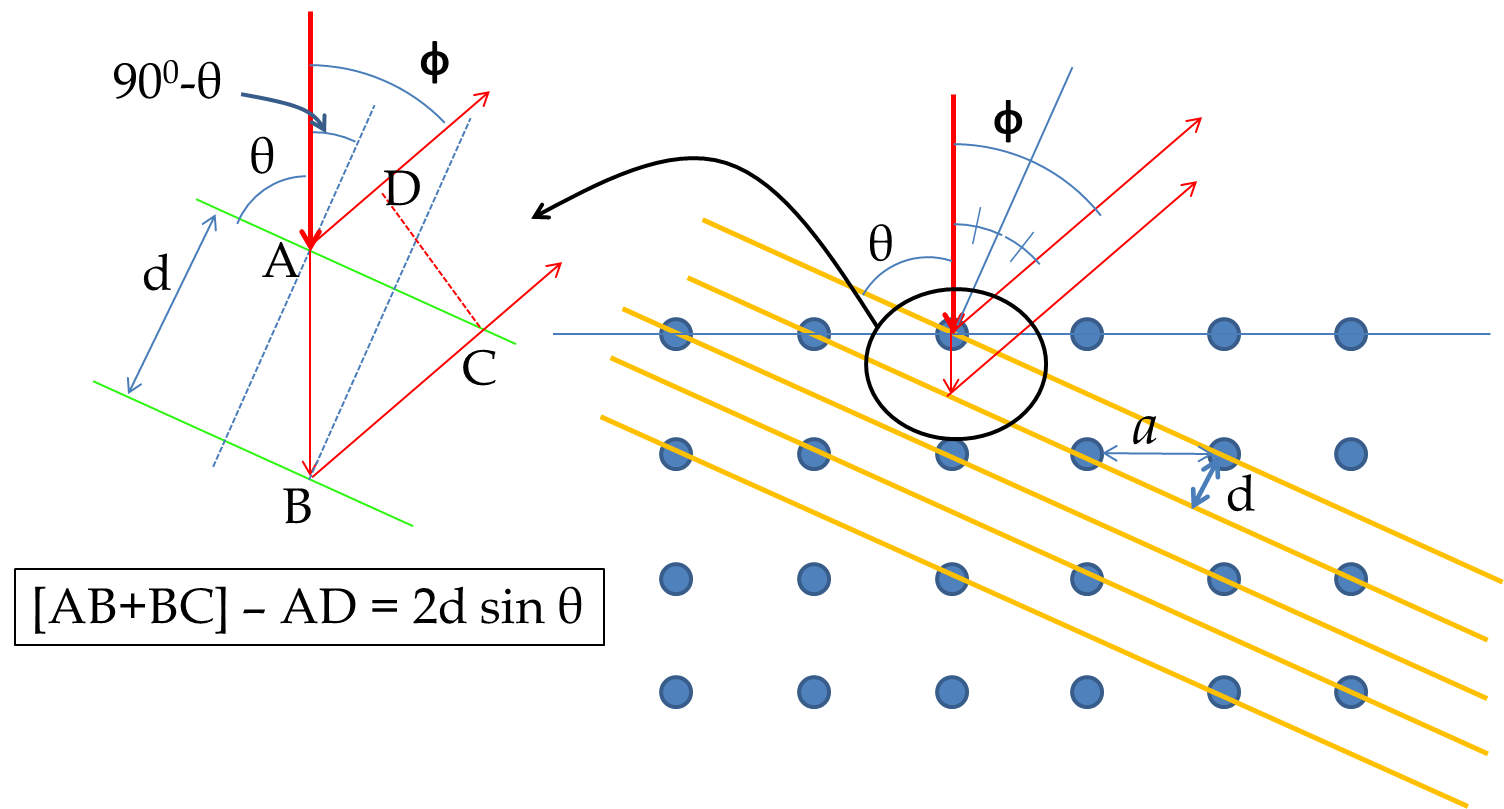
From figure,
\begin{equation*}
\cos\theta = \dfrac{d}{a}.
\end{equation*}
Therefore, the Bragg condition in terms of the inter-atomic spacing is
\begin{equation*}
2 a \sin\theta \cos\theta= n \lambda.
\end{equation*}
We can rewrite the left side in terms of the angle \(\phi\) used in Davisson-Germer experiment as follows
\begin{equation*}
2 a \sin\theta \cos\theta= a \sin 2\theta = a\sin(180^{\circ}-\phi)= a\sin\phi.
\end{equation*}
Therefore, the Bragg condition becomes,
\begin{equation*}
a\sin\phi = n \lambda,\quad n = 0, 1, 2, \cdots.
\end{equation*}
Does the intensity peak for the 54 eV electron at \(50^{\circ}\) agree with this formula? Let us first calculate the wavelength of the electron of energy \(54 \text{ eV}\text{.}\)
\begin{equation*}
\lambda = \dfrac{h}{p} = \dfrac{h}{\sqrt{2mK}} = 0.167\:\textrm{nm}.
\end{equation*}
If \(n=1\) for this peak, the \(a\) for \(50^{\circ}\) would correspond to the following value of \(a\text{.}\)
\begin{equation*}
a = \dfrac{\lambda}{\sin\phi} = \dfrac{0.167\:\textrm{nm}}{\sin 50^{\circ}} = 0.218\:\textrm{nm},
\end{equation*}
which is in an excellent agreement with \(0.215\:\textrm{nm}\) given above.
Subsection 51.2.2 G. P. Thomson’s Experiment
G. P. Thomson and associates sent beams of electrons through thin foils of gold, aluminum, celluloid, and platinum, and found that when the films were thin enough so that multiple scatterings were limited the scattered rays formed rings around the central beam as illustrated in Figure 51.8. These rings occur as a result of diffraction from crystallites in the samples. Each crystallite diffracts at a particular angle and since they are oriented randomly in the sample, same diffraction angle in different direction make ring at the photographic plate. These diffractions are also called powder diffraction.
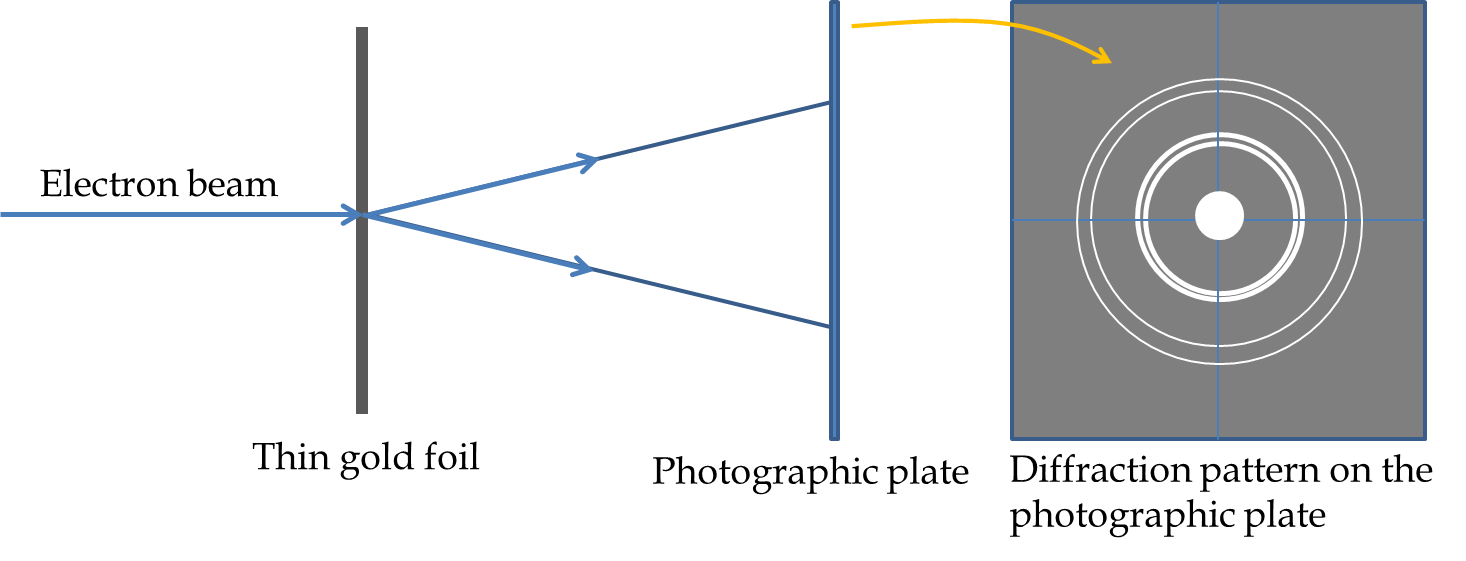
G. P. Thomson demonstrated that the diffraction rings from an \(X\)-ray diffraction and from a beam of electron with same energy as the \(X\)-ray are identical lending support to the wave nature of electron. Both Davisson and G. P. Thomson were awarded Nobel prizes in 1937 for their experiments demonstrating the wave nature of electron. It is interesting to note thar G. P. Thomson is son of J. J. Thomson who discovered electron particles in the Cathode rays while his son demonstrated the same particles to be waves.
Subsection 51.2.3 The Tonomura Experiment
What types of waves are electrons? The Davisson-Germer and G. P. Thomson’s experiments illustrated that a stream of electrons diffracted as waves similarly to the way \(X\)-rays diffracted from the crystals. But, how does a single electron act in these experiments? Dr. Akira Tonomura at Central Research Laboratory, Hitachi Ltd., Japan, conducted a double-slit interference experiment with single electrons. His apparatus was a modification of the electron microscope. Figure 51.9 shows schematics of the apparatus used by Tonomura. Electron from a field emission tip is accelerated to an energy of 50 keV energy and passed through a a two-slit arrangement made from a very fine wire filament between two plates. The wire filament is kept at a voltage of about 10 V relative to the plates. After an electron emerges from the other side of the double slit it is detected by amplifying the signal.
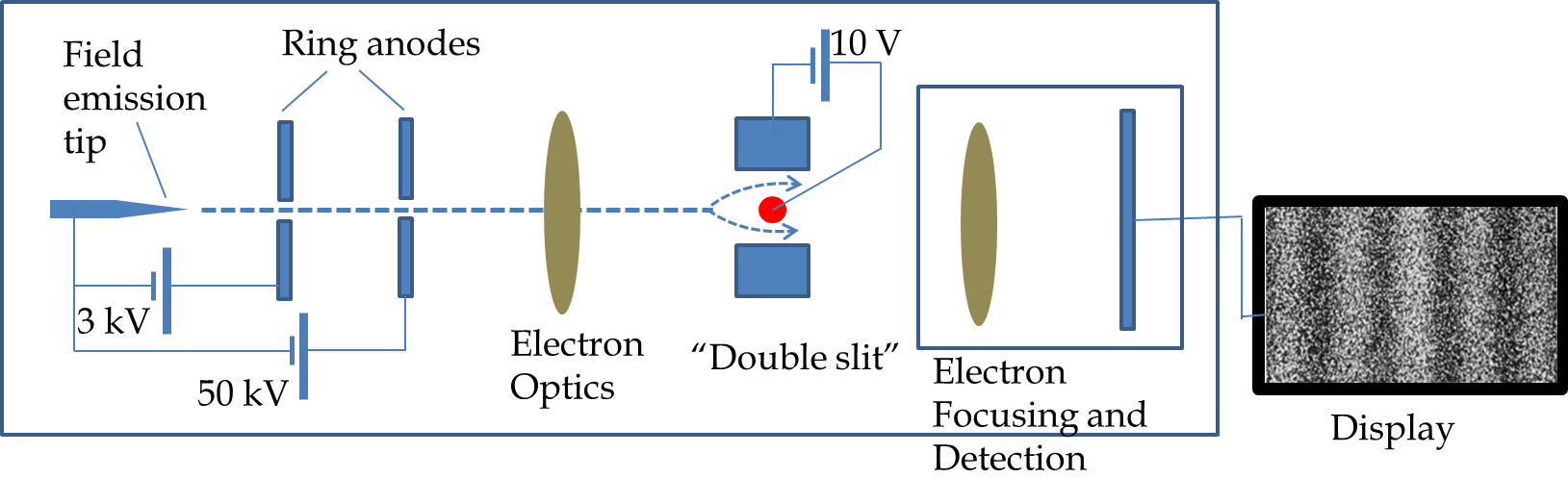
Tonumura’s results are shown in Figure 51.10. When an electron arrives at the detection screen the detector shows one dot for where the electron “landed” on the screen. Initially, the dots appear random but an interference pattern is clearly visible after a few thousand electrons have impacted the screen. If each electron goes through one side od the other, there would be an average uniform distribution of the dots on the screen. Somehow, a single electron goes through both sides at the same time. This would be the case if each electron is a wave of some kind. According to the interpretations of Schrödinger’s equation the wave of an electron is actually a probability amplitude wave.


