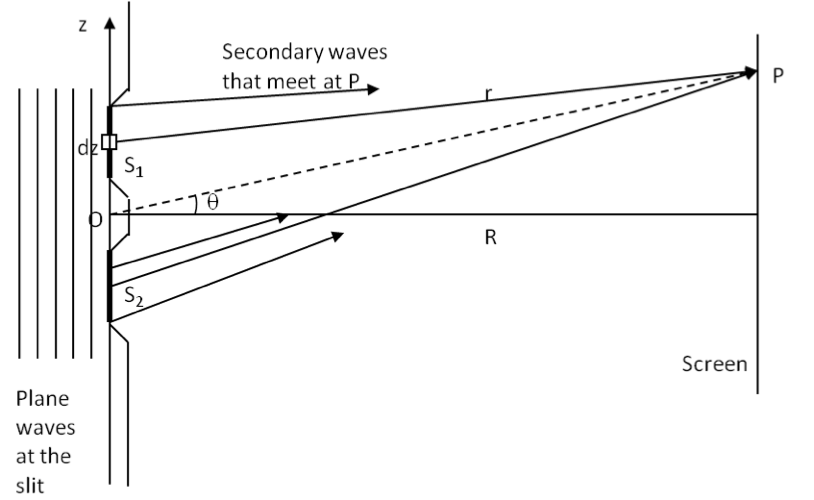
In the last chapter when we were studying interference in the Young’s double-slit experiment we ignored the diffraction effect in each slit. We assumed that the slits were so narrow that on the screen you only saw the interference of light from just two point sources.
Figure 48.11 in
Section 48.4 shows us that if width of a slit is less than one wavelength, then, there is just a spreading of light and no diffraction peaks or troughs on the screen. Therefore, it was reasonable to leave out the diffraction effect in the last chapter. That figure also illustrated that if you a slit wider than a wavelength, you cannot ignore diffraction effects.
We will use
Figure 48.16 for a basic arrangement of a double-slit experiment. The slits
\(\text{S}_1\) and
\(\text{S}_2\) have the same width
\(b\) and are separated by a center-to-center distance
\(a\text{.}\) Calculation in subsection
Subsection 48.5.1 gives the following expression for intensity in the direction
\(\theta\) when a plane wave of wavelength
\(\lambda\) is incident on the slits.
\begin{equation}
I(\theta) = I_0 \left(\frac{\sin\beta}{\beta} \right)^2\: \cos^2\alpha,\tag{48.17}
\end{equation}
where parameters \(\alpha\) and \(\beta\) are given by
\begin{align}
\amp \alpha \equiv \frac{\pi a \sin\theta}{\lambda}.\tag{48.18}\\
\amp \beta \equiv \frac{\pi b \sin\theta}{\lambda}.\tag{48.19}
\end{align}
The factor
\((\sin\beta/\beta)^2\) in intensity in Eq.
(48.17) comes from the diffraction of the waves originating from the same slit and the factor
\(\cos^2\alpha\) arises from the interference of the waves originating from two different slits. The intensity will be zero whenever either of these two have a value of zero. Since maxima of
\((\sin\beta/\beta)^2\) for its side peaks are much lower than the central peak, the peaks at further away from the center have less intensity maximum than peak at the center. Thus, we find that the peaks of
\(\cos^2\alpha\) are modulated by the peaks and valleys of
\((\sin\beta/\beta)^2\text{.}\)
The diffraction pattern has a minimum whenever \(I(\theta)\) becomes a minimum.
\begin{align}
\text{Minima:} \amp \notag\\
\amp \ \ \ \ \ \alpha = \pm\frac{\pi}{2}, \pm 3 \frac{\pi}{2}, \cdots\tag{48.20}\\
\amp \ \ \ \ \ \beta = \pm \pi, \pm 2 \pi, \pm 3 \pi, \cdots\tag{48.21}
\end{align}
The minima due to \(\alpha\) are called the interference minima and the ones due to \(\beta\) are called the diffraction minima. It is also useful to rewrite the minima conditions in terms of wavelength \(\lambda\) and slit dimensions \(a\) and \(b\text{.}\)
\begin{align}
\text{Minima:}\amp \notag\\
\amp \text{Interference:}\ \ \ \ \ a\sin\theta = \pm\frac{\lambda}{2}, \pm 3 \frac{\lambda}{2}, \cdots\tag{48.22}\\
\amp \text{Diffraction:}\ \ \ \ \ b\sin\theta = \pm \lambda, \pm 2 \lambda, \pm 3 \lambda, \cdots\tag{48.23}
\end{align}
The maxima due to interference occur at maxima of \(\cos^2\alpha\text{.}\) This give the maxima conditions to be at \(\alpha = m\pi\) with \(m\) being an integer. Writign this in angle \(\theta\) we get the following directions for interference maxima.
\begin{equation*}
\text{Interference Maxima: }\ a\sin\theta = m \lambda, \ \ m = 0, \pm 1, \pm 2, \cdots.
\end{equation*}
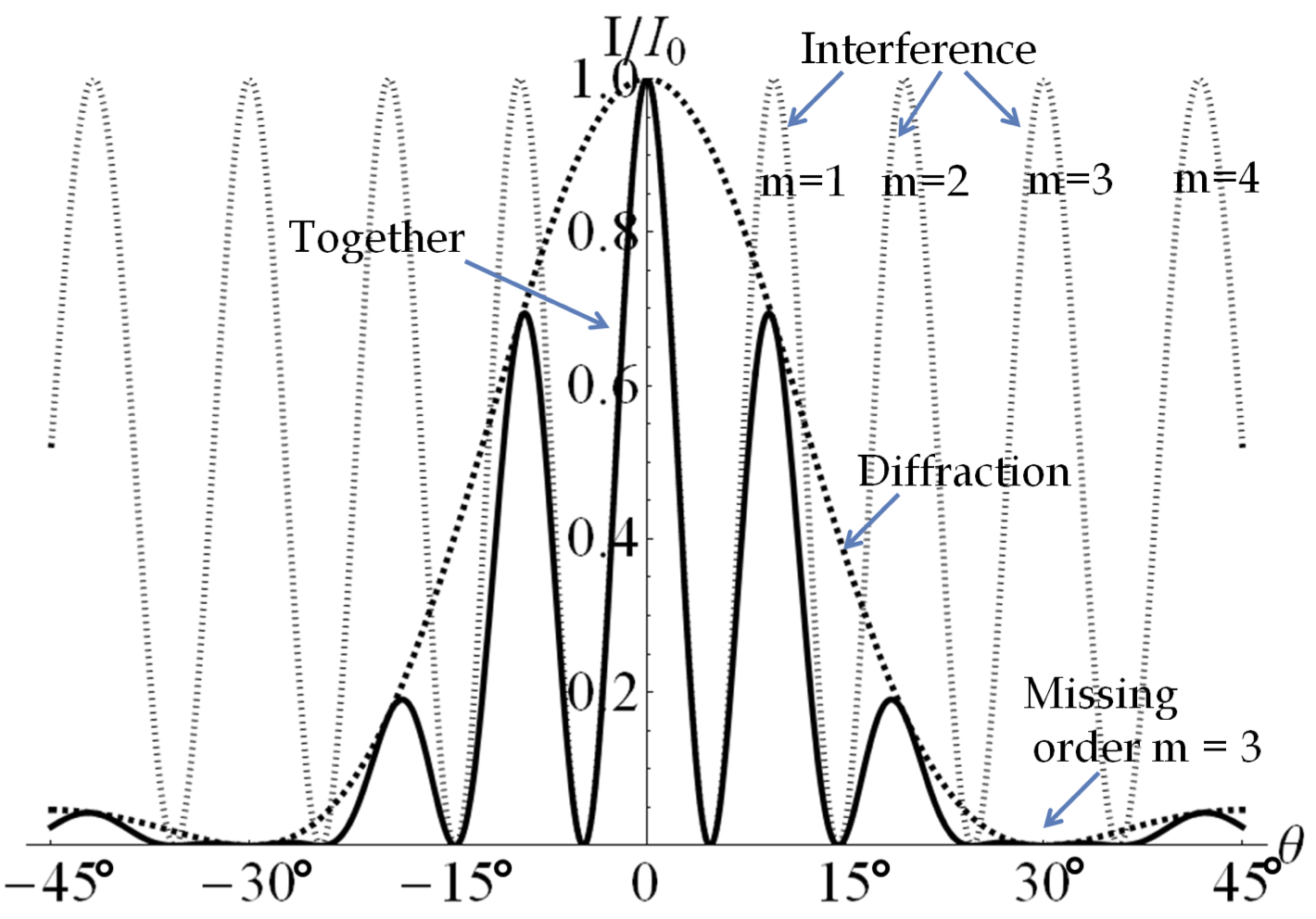
Some of these interference maxima would not show up on the screen if that direction also corresponds to a minimum for the diffraction. We refer to these missing peaks as missing order. Thus, if there exists an \(m^\prime\) for some \(m\) such that following two conditions hold true for the direction \(\theta\text{,}\) then, order \(m\) is said to be missing.
\begin{equation}
a\sin\theta = m \lambda\ \ \text{and}\ \ b\sin\theta = m^\prime \lambda.\tag{48.24}
\end{equation}
One example diffraction pattern on the screen is presented in
Figure 48.17. The solid line with multiple peaks of various heights is the intensity observed on the screen. It is a product of the interference pattern form waves from separate slits and the diffraction of waves from within one slit. The plot shows the expected result for a slit width
\(b = 2\lambda\) and slit separation
\(a = 6\lambda\text{.}\) The maximum corresponding to
\(m=\pm 3\) orders for the interference is missing because the minumum of the diffraction occurs in the same direction.