Section 38.9 Electromagnetic Effect Bootcamp
Exercises Exercises
Faraday’s Flux Rule and Lenz’s Law
1. Six Induced EMF and Lenz’s Law Exercises.
Follow the link: Exercise 38.3.7.1.
2. Induced Current in Loop Between Poles of an Electromagnet.
Follow the link: Exercise 38.3.7.2.
3. Induced Current in a Circular Wire Surrounding a Solenoid from Varying Current in the Solenoid.
Follow the link: Exercise 38.3.7.3.
4. (Calculus) Induced EMF in Two-loop Coil Surrounding a Solenoid with Sinusoidally Varying Current.
Follow the link: Exercise 38.3.7.4.
5. (Calculus) Induced Current As a Result of a Varying Magnetic Field.
Follow the link: Exercise 38.3.7.5.
Motional EMF
6. Induced EMF When Metal Bar Moving on U-shaped Rails.
Follow the link: Example 38.30.
7. Induced EMF in a Metal Bar Moving in an External Magentic Field.
Follow the link: Exercise 38.4.4.1.
EMF from Rotation
8. Induced EMF in a Rotating Ring in a Magnetic Field.
Follow the link: Example 38.36.
Faraday’s Law
9. (Calculus) Electric Field from a Varying Magnetic Field.
Follow the link: Example 38.41.
10. (Calculus) Induced Electric Field Outside from Varying Current in a Solenoid.
Follow the link: Example 38.45.
11. Electric Field Induced by a Magnetic Field Changing in Time with a Cylindrical Symmetry.
Follow the link: Exercise 38.7.3.1.
Miscellaneous
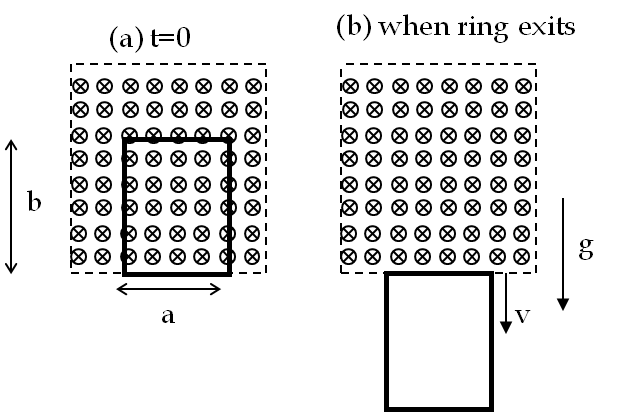
12. (Calculus) Copper Ring Falling and Exiting a Magnetic Field Region Near Earth.
A rectangular copper ring, of mass 100 g and resistance 0.2 \(\Omega\text{,}\) is in a region of uniform magnetic field that is perpendicular to the area enclosed by the ring and horizontal to earth surface. The ring is let go from rest when it is at the edge of the nonzero magnetic field region.
(a) Find its speed when the ring just exits the region of uniform magnetic field.
(b) If it was let go at \(t=0\text{,}\) what is the time when it exits the region of magnetic field for the following values \(a= 25\text{ cm}\) , \(b = 50\text{ cm}\text{,}\) \(B = 3\text{ T}\text{,}\) \(g = 9.8\text{ m/s}^2\text{?}\) Assume that the magnetic field of the induced current is negligible compared to \(3\text{ T}\text{.}\)
Hint.
(a) net force on the ring is from gravity on all of the ring and magnetic force on the top section of the ring. (b) Solve \(dy/dt = v_y\text{.}\)
Answer.
(a) \(v = \dfrac{g}{\omega}\:\left(1 - e^{-\omega t} \right)\text{,}\) (b) 2.9 sec.
Solution 1. (a)
(a) There are two forces on the ring when it is exiting the region of non-zero magnetic field - one force is the weight and the other the magnetic force on the induced current. The net magnetic force on the ring will come from the force on the upper wire since the forces on the left and right wires will cancel each other and the lower wire does not see any magnetic field. The net magnetic force will be upward since the induced current will have the direction left-to-right in the upper wire and the magnetic field is pointed in the page.
Let us point the positive \(y\)-axis down, then we find that the \(y\)-component of the acceleration of the wire frame will be given by
\begin{equation*}
m\dfrac{dv_y}{dt} = -I_{\text{ind}}\: a\: B_{\text{ext}} + m g,\ \ \ \ (1)
\end{equation*}
where \(m\) is the mass, \(I_{\text{ind}}\text{,}\) the induced current, and \(B_{\text{ext}}\) the external magnetic field. To solve this equation for \(v_y\) we need an expression for \(I_{\text{ind}}\text{.}\) We can obtain this by applying Faraday’s law to the loop.
Let the lower part of the wire frame be at the coordinate \(y(t)\) at time \(t\text{.}\) Then the flux through the loop at this instant will have the following expression.
\begin{equation*}
\Phi(t) = a (b-y) B_{\text{ext}},
\end{equation*}
Now, taking the time derivative of this will give the rate at which flux changes, which will be equal to the induced EMF, \(\mathcal{E}_{\text{ind}}\text{.}\)
\begin{equation*}
\mathcal{E}_{\text{ind}} = \left|\dfrac{d\Phi}{dt} \right| = aB_{\text{ext}} \left|\dfrac{d y}{dt}\right|.
\end{equation*}
Now, we divide this by the resistance \(R\) of the wire making up the loop.
\begin{equation*}
I_{\text{ind}} = \dfrac{aB_{\text{ext}} |v_y|}{R}.
\end{equation*}
Since \(v_y\) is positive here we will have \(|v_y| = v_y\text{,}\) and obtain the following for the induced current.
\begin{equation*}
I_{\text{ind}} = \dfrac{aB_{\text{ext}} v_y }{R}. \ \ \ \ (2)
\end{equation*}
Now, putting (2) into (1) we obtain
\begin{equation*}
m\dfrac{dv_y}{dt} = -\dfrac{a^2 B_{\text{ext}}^2} {R}\: v_y + m g.
\end{equation*}
Dividing both sides by \(m\) gives
\begin{equation*}
\dfrac{dv_y}{dt} = -\dfrac{a^2 B_{\text{ext}}^2} {mR}\: v_y + g.\ \ \ \ (3)
\end{equation*}
The quantity multiplying \(v_y\) on the right side has dimensions of 1/time, which is a unit of frequency. Let us denote the coefficient of \(v_x\) by \(\omega\text{.}\)
\begin{equation*}
\omega \equiv \dfrac{a^2 B_{\text{ext}}^2} {mR}.\ \ \ \ (4)
\end{equation*}
Rewriting Eq. (3) we have
\begin{equation*}
\dfrac{dv_y}{dt} = -\omega\: v_y + g.
\end{equation*}
We now solve this equation by separating the variables on the two sides of equlity,
\begin{equation*}
\dfrac{dv_y}{-\omega\: v_y + g} = dt.
\end{equation*}
Integrating this equation from \((t=0,\ v_y = 0)\) to \((t=t, v_y = v_y)\) we get
\begin{equation*}
\int_0^{v_y}\: \dfrac{dv_y}{-\omega\: v_y + g} = \int_0^t\: dt.
\end{equation*}
The result can be written as
\begin{equation*}
v_y = \dfrac{g}{\omega}\:\left(1 - e^{-\omega t} \right). \ \ \ \ (5)
\end{equation*}
Since the ring has no other component of the velocity, the speed of the ring at time \(t\) while some part of the ring is still within the region of non-zero magnetic field will be
\begin{equation*}
v = |v_y| = \dfrac{g}{\omega}\:\left(1 - e^{-\omega t} \right).
\end{equation*}
Solution 2. (b)
(b) Writing \(v_y = dy/dt\) transforms equation (5) to the following equation for the \(y\)-coordinate of the bottom part of the ring.
\begin{equation*}
\dfrac{dy}{dt} = \dfrac{g}{\omega}\:\left(1 - e^{-\omega t} \right).
\end{equation*}
Denote the height of the ring by letter \(b\text{.}\) We can integrate this from \(y=0\) to \(y=b\) to find the time for the ring to exit the magnetic field region.
\begin{equation*}
\int_0^b\: dy = \dfrac{g}{\omega}\:\int_0^T\:\left(1 - e^{-\omega t} \right) dt.
\end{equation*}
This results in the following equation for the time \(T\text{.}\)
\begin{equation*}
b-\dfrac{g}{\omega^2}\: e^{-\omega T} = \dfrac{g}{\omega}\: T.\ \ \ \ \ (6)
\end{equation*}
This equation can be solve graphically. The values given in the problem statement give us the following values for the constants in this equation.
\begin{align*}
\amp \omega = \dfrac{a^2 B^2}{m R} = \dfrac{0.25^2 \times 3^3}{0.1\times 0.1} = 55.25\:\text{s}^{-1},\\
\amp \dfrac{g}{\omega} = 0.1\:\text{m/s},\ \ \dfrac{g}{\omega^2} = 0.003\:\text{m},\ \ b = 0.5\:\text{m}.
\end{align*}
For these values, the second term on the left side in Eq. (6) will be negligible compared to the first term. Ignoring the second term gives us a simpler equation to solve.
\begin{equation*}
b \approx \dfrac{g}{\omega}\: T\ \ \Longrightarrow\ \ T = \dfrac{b\omega}{g} = 2.9\:\text{s}.
\end{equation*}
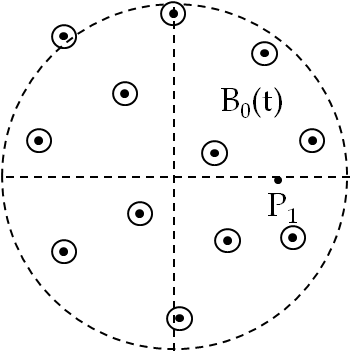
13. (Calculus) Accelerarting Proton by Induced Electric Field in a Region of Changing Magnetic Field.
A time-dependent but otherwise uniform magnetic field of magnitude \(B(t)\) is confined in a cylindrical region of radius \(5\text{ cm}\text{.}\) Initially magnetic field is in the region has a magnitude of \(3\text{ T}\) but it is decreasing at the rate of \(400\text{ G/s}\text{.}\) An electric field is induced in this space due to changing magnetic field which causes acceleration of charges at rest. Find the direction and magnitude of acceleration of a proton placed at \(\text{P}_1\) which is \(3\text{ cm}\) from the center.
Hint.
Think of Faraday’s law as Ampere’s law for electric field.
Answer.
\(1.15\times 10^{5}\:\text{m/s}^2\text{.}\)
Solution.
We can treat Fararay’s law as an “Ampere’s law for E-field” with \(d\Phi/dt\) taking the role of current. Since the magnetic flux has a cylindrical symmetry we use a circular “Amperian loop” of radius \(r\text{.}\) The integration of the electric field around the loop gives
\begin{equation*}
2\pi r E = \left|\dfrac{d\Phi}{dt} \right|= \pi r^2 \left|\dfrac{dB}{dt}\right|.
\end{equation*}
Therefore,
\begin{equation*}
E = \dfrac{r}{2}\left|\dfrac{dB}{dt}\right|.
\end{equation*}
The electric field will circulate in circles around the axis. If you observe from the side in which the magnetic field points, here out-of-page and if the magnetic field is decreasing, then the electric field lines will have a counter-clockwise sense.
Let us find the magnitude of the electric field for the given numerical values.
\begin{equation*}
E = \dfrac{0.03\:\text{m}}{2}\times 400 \times 10^{-4}\:\text{T/s} = 12\times 10^{-4}\:\text{N/C}.
\end{equation*}
This electric field will act on the proton and cause the electron to accelerate with the value
\begin{align*}
a \amp = \dfrac{e\:E}{m_p} \\
\amp = \dfrac{1.6\times 10^{-19}\:\text{C}\times 12\times 10^{-4}\:\text{N/C}}{1.67\times 10^{-27}\:\text{kg}}\\
\amp = 1.15\times 10^{5}\:\text{m/s}^2.
\end{align*}
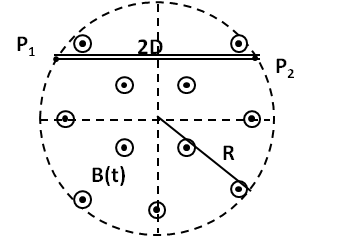
14. (Calculus) Induced EMF in a Conducting Rod Placed in a Changing Magnetic Field.
A time-dependent uniform magnetic field of magnitude \(B(t)\) is confined in a cylindrical region of radius \(R\text{.}\) A conducting rod of length \(2D\) is placed in the region as shown in the figure. Show that the EMF between the ends of the rod is give by \((dB/dt)D\sqrt{R^2-D^2}\text{.}\)
Hint.
Treat Faraday’s law as “Amepre’s law for the E-field”.
Answer.
Already in problem statement.
Solution.
Treating Faraday’s law as “Amepre’s law for the E-field” and taking a circular loop with radius \(r\) as the Amperian loop for the line integral of \(\vec E\) we arrive at
\begin{equation*}
2\pi r E = \left|\dfrac{d\Phi}{dt} \right|= \pi r^2 \left|\dfrac{dB}{dt}\right|.
\end{equation*}
Therefore,
\begin{equation*}
E = \dfrac{r}{2}\left|\dfrac{dB}{dt}\right|.
\end{equation*}
The electric field will circulate in circles around the axis. If you observe from the side in which the magnetic field points, here out-of-page and if the magnetic field is decreasing, then the electric field lines will have a counter-clockwise sense.
To find the EMF between the ends we need to integrate from \(\text{P}_1\) to \(\text{P}_2\text{.}\) The problem is that while the path is parallel to \(x\)-axis, the electric field is tangential to the circle with center at the center of the magnetic field region. To find an explicit expression for \(\vec E\cdot d\vec r\) we write the electric field analytically using the unit vector \(\hat u_{\theta}\text{.}\)
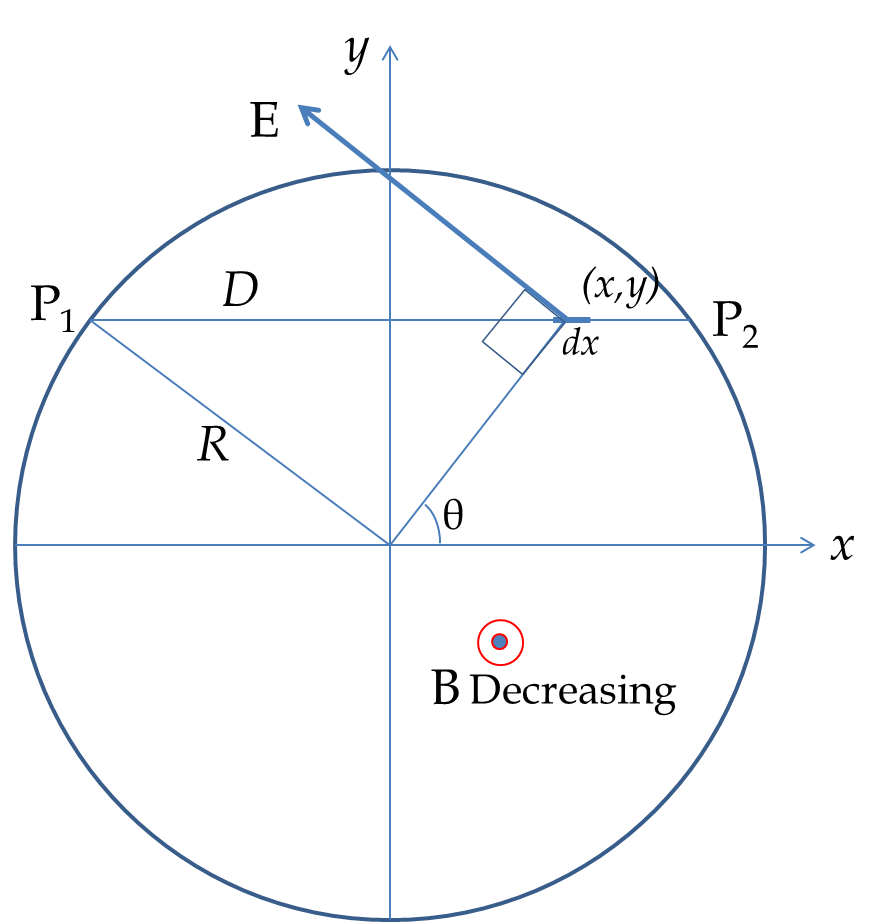
For a situation in which the magnetic field pointed towards the \(z\)-axis is decreasing we will get
\begin{equation*}
\vec E = \dfrac{r}{2}\left|\dfrac{dB}{dt}\right|\ \hat u_{\theta},
\end{equation*}
where \(\hat u_{\theta}\) for a point which is at an angle \(\theta\) with respect to the \(x\)-axis would be
\begin{equation*}
\hat u_\theta = -\sin\theta\:\hat i + \cos\theta\:\hat j.
\end{equation*}
An element of the the path here will have
\begin{equation*}
d\vec l = \hat i\:dx.
\end{equation*}
Therefore, the dot product will be
\begin{equation*}
\vec E \cdot d\vec l = - \dfrac{r}{2}\left|\dfrac{dB}{dt}\right| \: \sin\theta\: dx =
\end{equation*}
We can replace \(r\sin\theta\) by \(y\) and writing this in \((x,y)\) of the element
\begin{equation*}
\vec E \cdot d\vec l = - \dfrac{1}{2}\left|\dfrac{dB}{dt}\right| \: y\: dx
\end{equation*}
Here \(y\) is fixed on the path, given by \(y = \sqrt{R^2-D^2}\text{.}\) We integrate this from \(x=-D\) to \(x=D\) to obtain the difference in potential at the two points.
\begin{equation*}
\Delta \phi = \left|\dfrac{dB}{dt}\right| \: D\: \sqrt{R^2-D^2}
\end{equation*}

