Section 26.8 Clausius’s Theorem
Clausius’s theorem states that the following inequality holds for all cyclic processes.
\begin{equation}
\oint \frac{dQ}{T}\le 0. \tag{26.21}
\end{equation}
Proof:
Consider an arbitrary system X that undergoes a cyclic process. In each cycle the system receives or gives up heat to a set of thermal baths at temperatures \(T_1\text{,}\) \(T_2\text{,}\) \(\cdots\text{,}\) \(T_n\text{.}\) A Carnot engine is an example of this kind of system with only two heat baths where every process is reversible. Here we assume that some or all of the processes of X may be irreversible. Let \(Q_1\text{,}\) \(Q_2\text{,}\) \(\cdots\text{,}\) \(Q_n\) be the heat exchanged by X and the thermal baths at \(T_1\) , \(T_2\) , \(\cdots\) , \(T_n\) respectively with the sign notation that \(Q_i\) will be positive if heat flows in X and negative if heat flows out of X to a thermal bath. We will prove that
\begin{equation}
\sum_{i=1}^n \frac{Q_i}{T_i} \le 0. \tag{26.22}
\end{equation}
Once we have proved this, we can immediately obtain the theorem by considering the case where the system exchanges heat with infinitely many baths. In that case the sum in Eq. (26.22) will turn into integral in Eq. (26.21).
To proceed with the proof, we introduce reversible engines such as Carnot engines \(C_1\text{,}\) \(C_2\text{,}\) \(\cdots\text{,}\) \(C_n\) between the baths and a common heat bath at temperature \(T_0\) as shown in Figure 26.12.
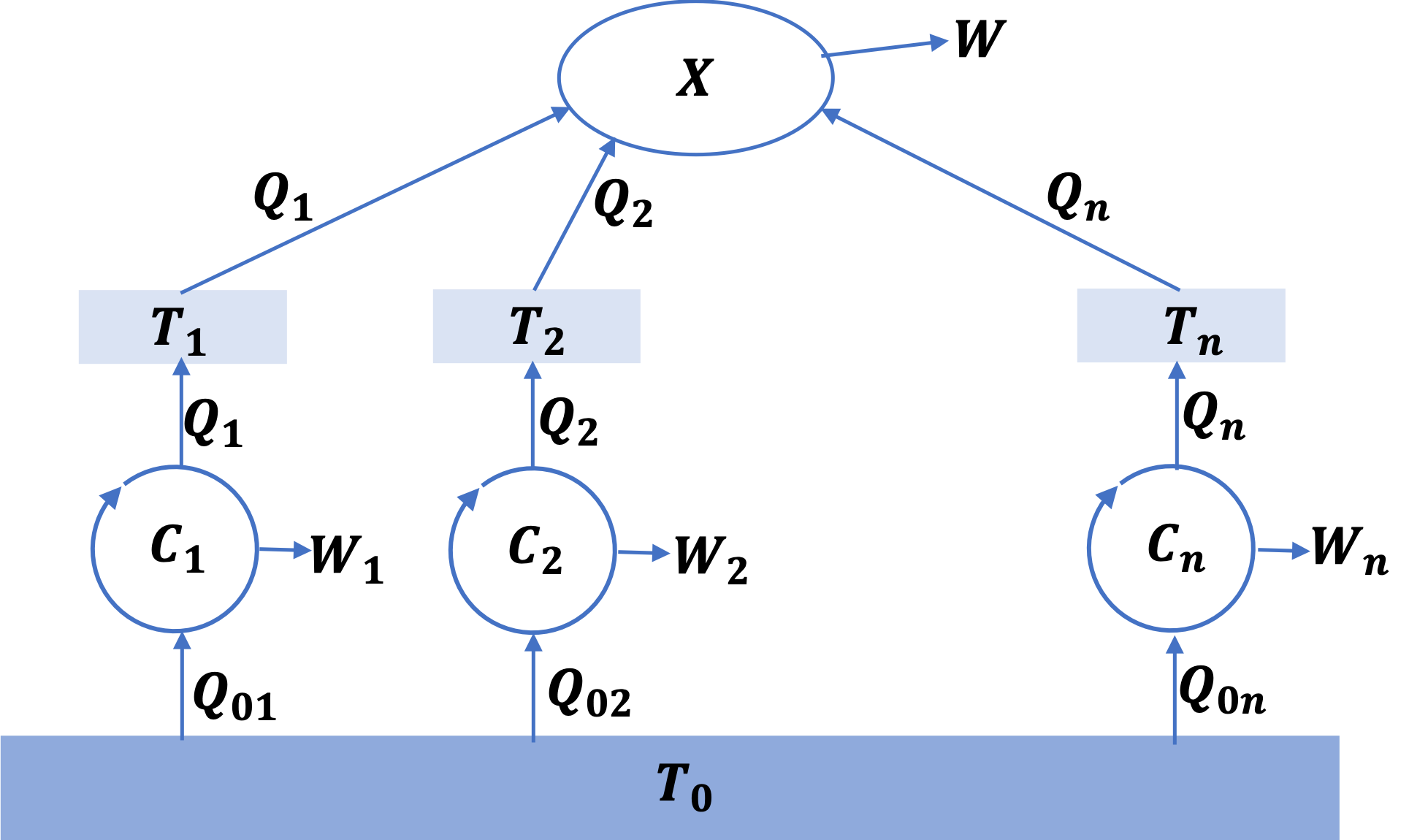
We will pick Carnot engines such that the \(i^\text{th}\) Carnot cycle replenishes heat exchanged by the \(i^\text{th}\) heat bath and X. Each Carnot cycle has the following relation between its temperatures of operation and the corresponding heat exchanged.
\begin{align*}
\amp C_1:\ \ \ \ Q_{01} = \frac{Q_1}{T_1}T_0, \\
\amp C_2:\ \ \ \ Q_{02} = \frac{Q_2}{T_2}T_0,\\
\amp \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \\
\amp C_n:\ \ \ \ Q_{0n} = \frac{Q_n}{T_n}T_0.
\end{align*}
Now if we look at one cycle of the complex system consisting of X and the carnot cycles \(C_1\text{,}\) \(C_2\text{,}\) \(\cdots\text{,}\) \(C_n\text{,}\) we find that it absorbs a net heat
\begin{equation*}
Q_0 = Q_{01} + Q_{02} + \cdots + Q_{0n},
\end{equation*}
and does the same amount of work. Therefore the complex system [X, \(C_1\) , \(C_2\) , \(\cdots\) , \(C_n\)] will violate the Kelvin-Planck statement of the second law of thermodynamics if heat \(Q_0\) was positive. That would mean a net intake of heat to the system in one cycle all of which converted to work without any other change, which, according to the second law, cannot happen. Therefore, second law forbids \(Q_0\) from being positive. Hence,
\begin{equation*}
Q_0 = \sum_{i=1}^{n} \frac{Q_i}{T_i} T_0 \le 0.
\end{equation*}
Since \(T_0>0\) , we obtain the desired result.
\begin{equation*}
\sum_{i=1}^n \frac{Q_i}{T_i} \le 0.
\end{equation*}
Considering the case where system X exchanges infinitesimal amount of heat with infinitely many baths turns the sum into integral over the cycle of the system:
\begin{equation*}
\oint \dfrac{dQ}{T}\le 0\text{.}
\end{equation*}

