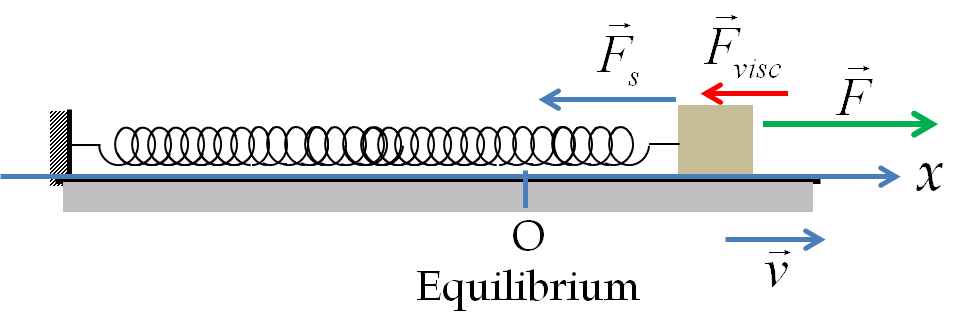
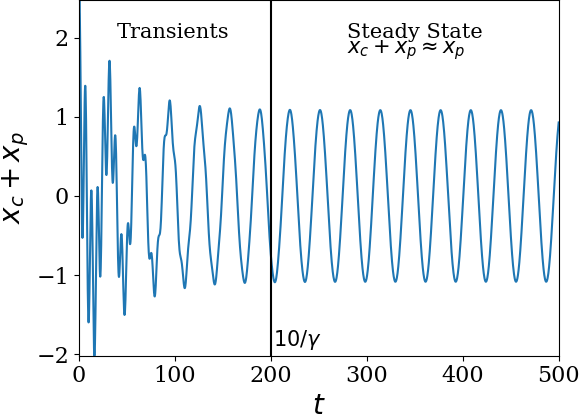
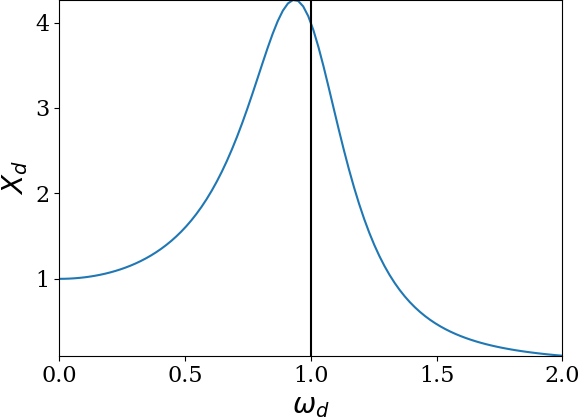
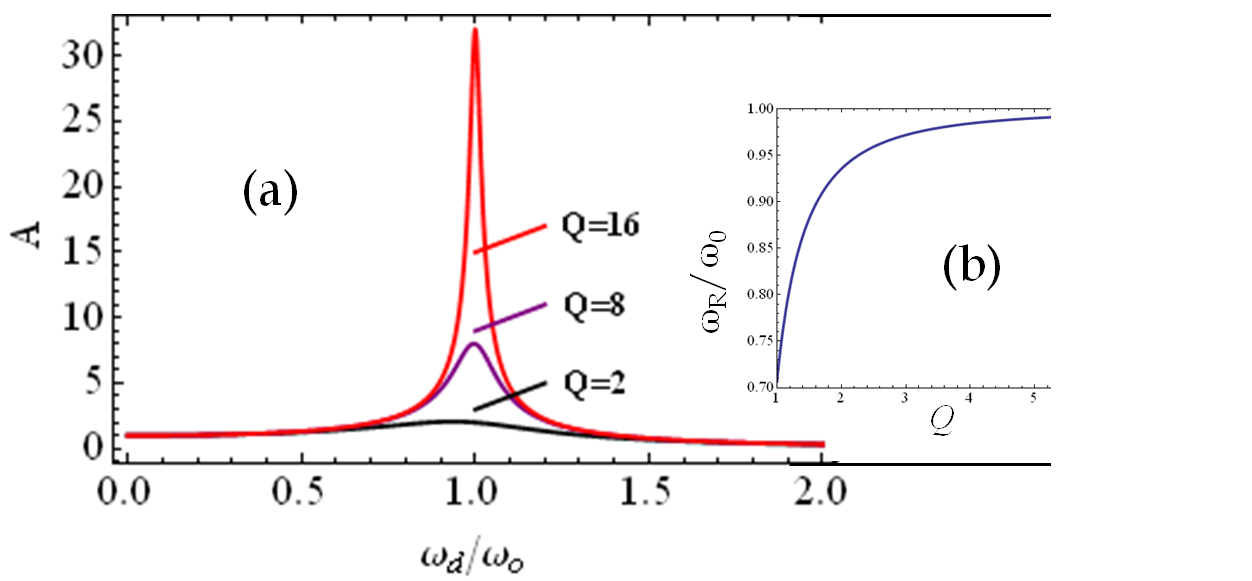
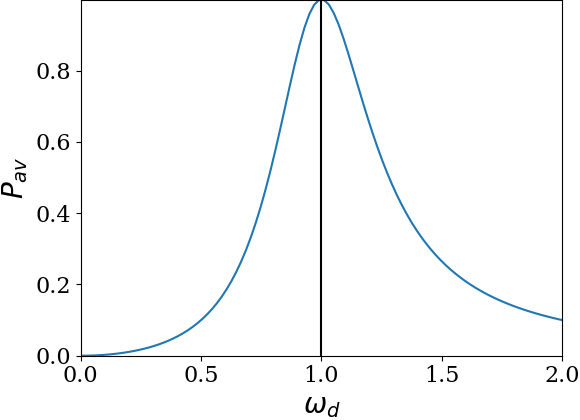
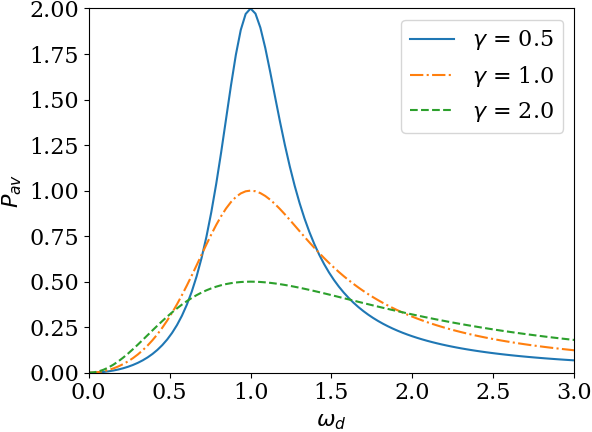
Remark 13.44. Calculations for Eq. (13.87).
Here we give you details of the work that you should verify.
\begin{align*}
\amp P_\text{av}(\omega_d) = \frac{F_0^2}{2\, m\, \gamma}
\end{align*}
This gives
\begin{equation*}
\omega_d^4 - \left( 2\omega_0^2 + \gamma^2\right)\,\omega_d^2 + \omega_0^4 = 0.
\end{equation*}
Let \(x=\omega_d^2\) and solve the quadratic equation for \(x\text{.}\)
\begin{align*}
\omega_d^2 \amp = \frac{1}{2} \left[ \left( 2\omega_0^2 + \gamma^2 \right) \pm \sqrt{ \left( 2\omega_0^2 + \gamma^2 \right)^2 - 4 \omega_0^4 } \right] \\
\amp = \omega_0^2 + \frac{1}{2} \gamma^2 \pm \omega_0\gamma \sqrt{ 1 + \frac{\gamma^2}{4 \omega_0^2} } \\
\amp \approx \omega_0^2 \pm \omega_0\gamma \left( 1 \right) \ \ \ \text{since } (\gamma/\omega_0) \ll 1.
\end{align*}
Now, we take square root to get
\begin{equation*}
\omega_d = \pm \sqrt{ \omega_0^2 \pm \omega_0\gamma }.
\end{equation*}
Looking at the positive root (negative root gives same range.) we have
\begin{align*}
\omega_d \amp = \sqrt{ \omega_0^2 \pm \omega_0\gamma } \\
\amp = \omega_0 \left( 1 \pm \frac{\gamma}{\omega_0} \right)^{1/2}\\
\amp \approx \omega_0 \left( 1 \pm \frac{1}{2}\,\frac{\gamma}{\omega_0} \right) \\
\amp = \omega_0 \pm \frac{1}{2}\,\gamma
\end{align*}
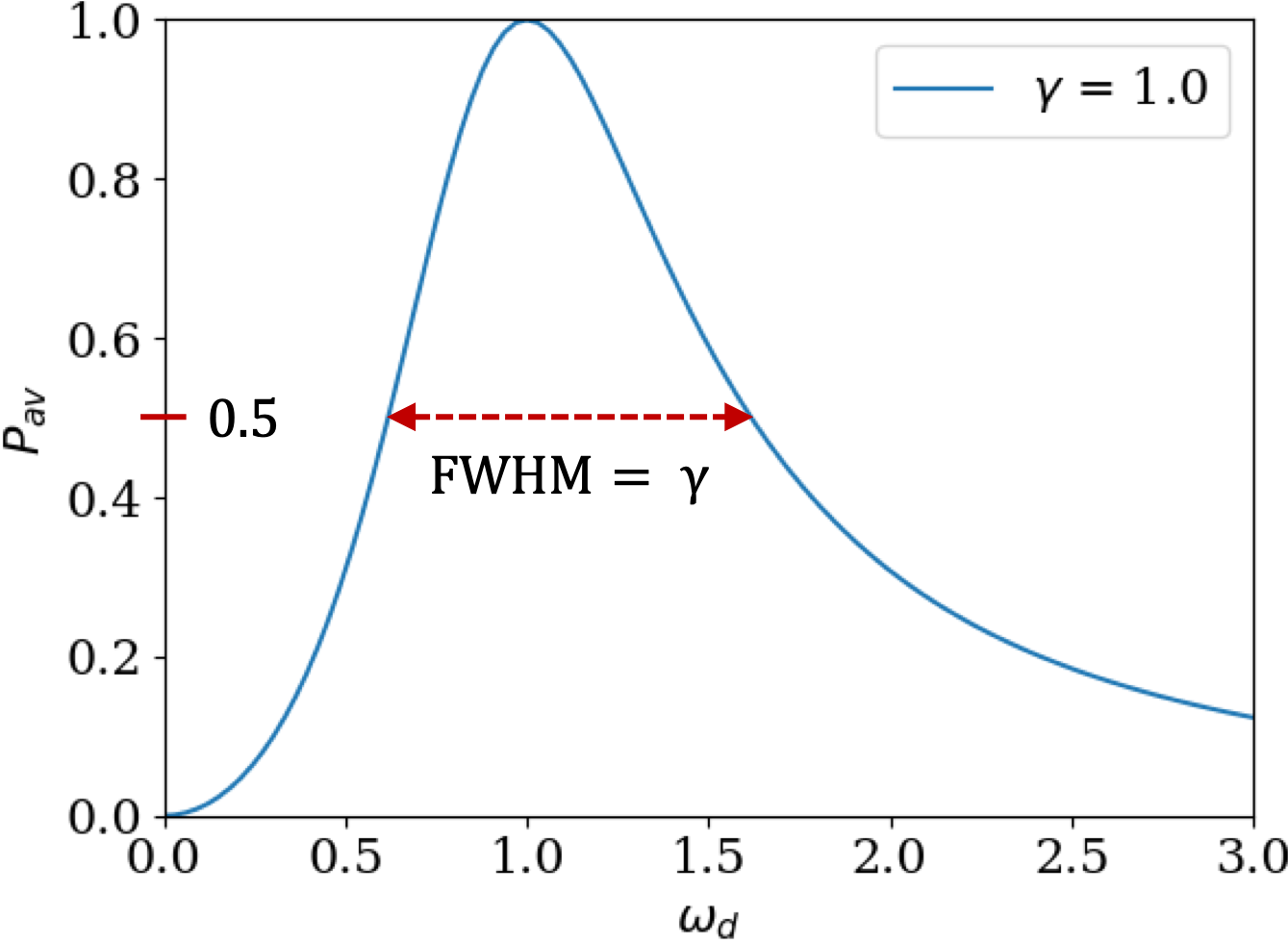
Thus, the value of \(\omega_d\) at half maximum has two values around the peak; let’s call them left and right values.
\begin{align*}
\amp \left( \omega_d \right)_\text{left} = \omega_0 - \frac{\gamma}{2}.\\
\amp \left( \omega_d \right)_\text{right} = \omega_0 + \frac{\gamma}{2}.
\end{align*}
Hence, the width at half maximum is
\begin{equation*}
\text{FWHM} = \left( \omega_d\right )_\text{right} - \left(\omega_d \right)_\text{left} = \gamma.
\end{equation*}