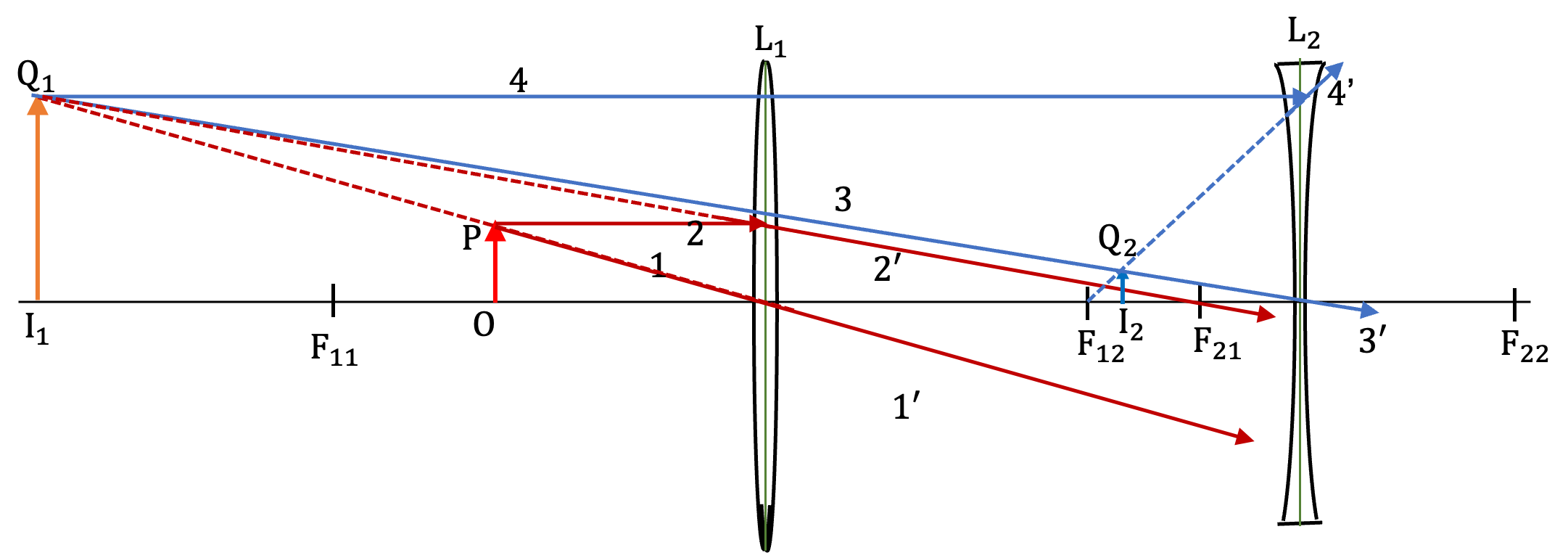
1. Image by Two Convex Lenses.
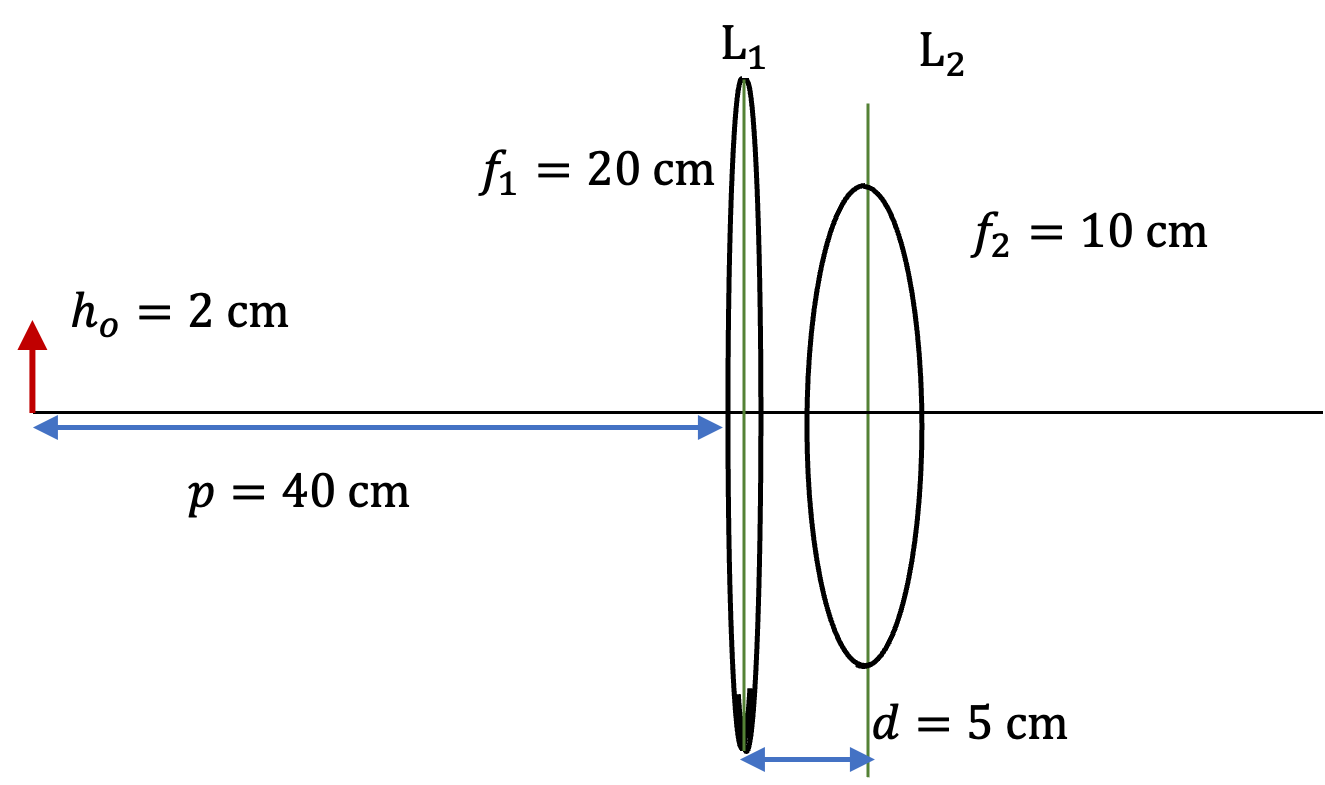
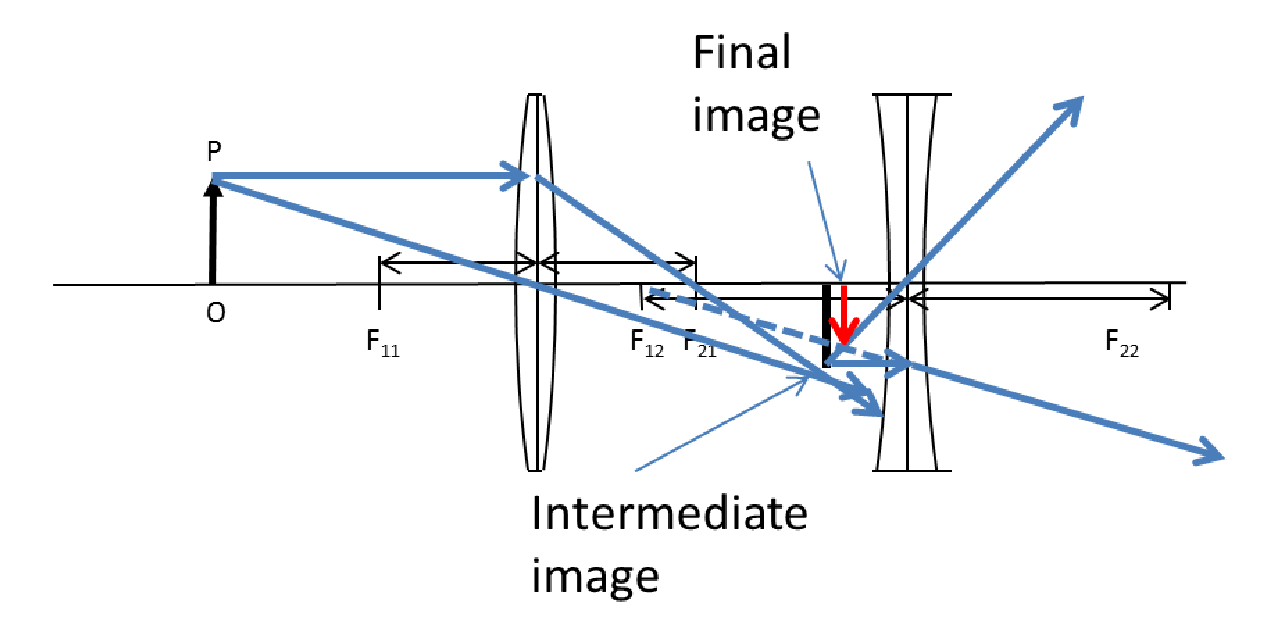
Two convex lenses of focal lengths \(20\text{ cm}\) and \(10\text{ cm}\) are placed \(30\text{ cm}\) apart as shown in Figure 44.65. An object of height \(2\text{ cm}\) is placed \(10\text{ cm}\) in front of the lens of the focal length \(20\text{ cm}\text{.}\) Find the location, orientation and magnification factor of the final image.
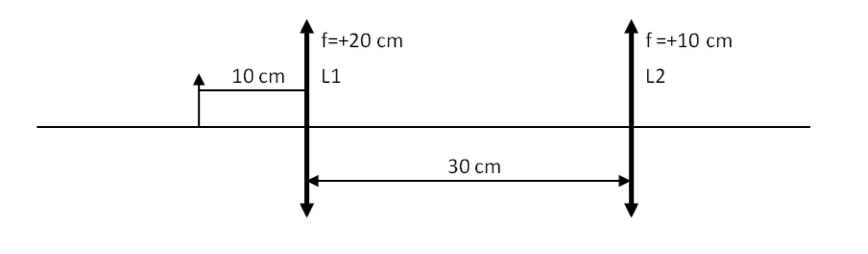
Hint.
Work one lens at a time.
Answer.
\(12.5\ \text{cm}\) back of lens L2, inverted, half the size, \(h_i = 1.0 \text{ cm}\text{.}\)
Solution.
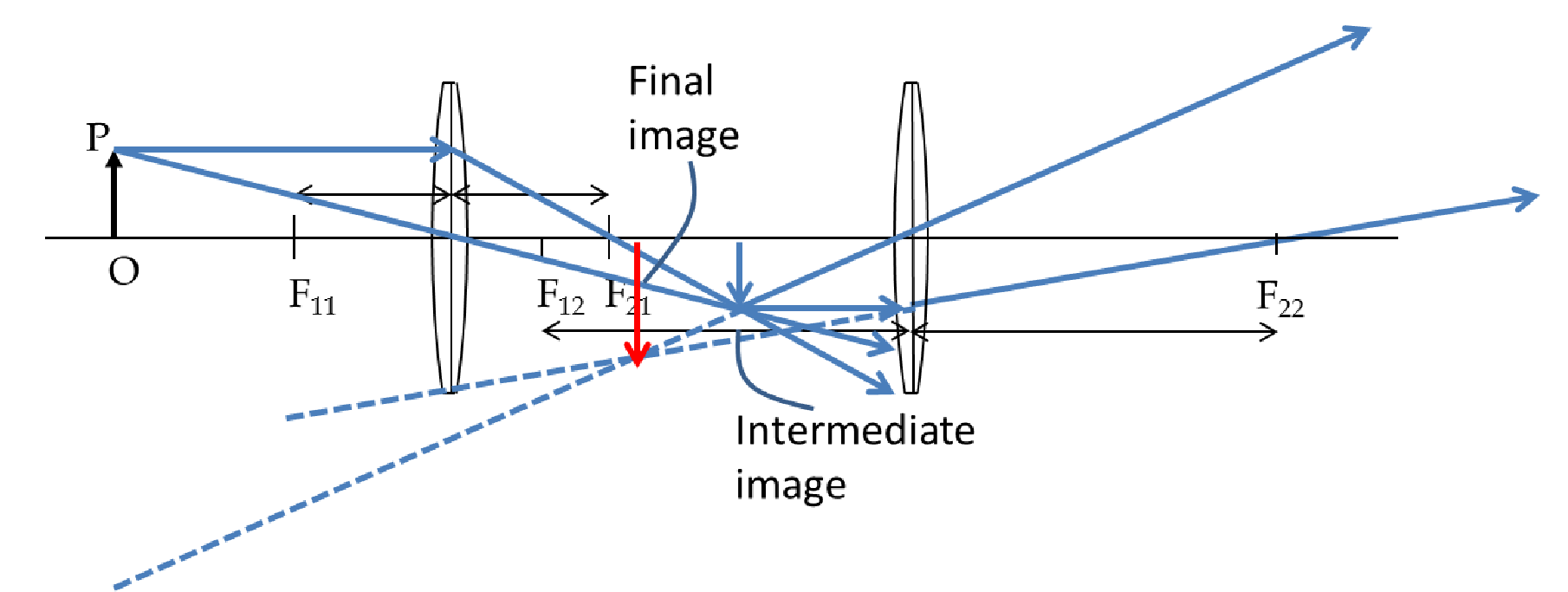
We will work one lens at a time. First we find the image from lens L1 and use this image as object for lens L2. We have the following for lens L1.
\begin{equation*}
p = +10\ \text{cm},\ \ f = + 20\ \text{cm}.
\end{equation*}
Therefore, the image distance \(q_1\) will be
\begin{equation*}
\frac{1}{q} = \frac{1}{20\ \text{cm}} - \frac{1}{10\ \text{cm}} = -\frac{1}{20\ \text{cm}} \ \ \Longrightarrow q_1 = -20\text{ cm}.
\end{equation*}
Therefore, the image by lens L1 will be virtual and at \(20\text{ cm}\) to the left of the L1.
Now, we take the image from L1 and treat it like an object for lens L2. To get the object distance to L2, we need to include the distance between the lenses also.
\begin{equation*}
p_2 = |q_1| + d = 20\text{ cm} + 30\text{ cm} = 50\text{ cm}.
\end{equation*}
with \(f_2= + 10\text{ cm}\text{,}\) we get
\begin{equation*}
\ \frac{1}{q_2} = \frac{1}{10\ \text{cm}} - \frac{1}{50\ \text{cm}}\ \ \Longrightarrow\ \ q_2 = 12.5\ \text{cm}.
\end{equation*}
Therefore, the location of the final image is \(12.5\ \text{cm}\) back of lens L2.
To find the net magnification, we find magnification in each lens and then multily them.
\begin{align*}
\amp m_1 = -\frac{q_1}{p} = -\frac{-20\ \text{cm}}{10\ \text{cm}} = + 2. \\
\amp m_2 = -\frac{q_2}{p_2} = -\frac{12.5\ \text{cm}}{50\ \text{cm}} = - 1/4. \\
\amp m = m_1\times m_2 = -\frac{1}{2}.
\end{align*}
Hence, the final image is inverted and is half the size of the original object. That, is the size of the image is \(1\text{ cm}\text{.}\)