Section 14.12 Reflection and Transmission
So far we have studied waves traveling in an open space in a single medium. Since wave speed depends on the chanracteristics of the media, if a wave encounters another medium, there will be a reflection of the wave back into the first medium and some transmission into the second medium as illustrated in Figure 14.40 for waves on a string with two different cords, which are the two media for the wave.
Turning on the vibrator, shown on the left end of the figure by a triangle, sends a wave towards the knot. We call this wave the incident wave. When the wave arrives at the knot, the knot is vibrated by the incoming wave. As a result the knot acts as a wave transmitter sending waves in the two directions, one in the second string, the transmitted wave and the other in the first string, the reflected wave which moves in the opposite direction to the wave coming from the vibrator. The reflected wave will come back and strike the vibrator. We will assume that strings are very long and we are looking at times when reflected wave has not struck the vibrator yet. Similarly, we assume that transmitted wave has not struck the other end.
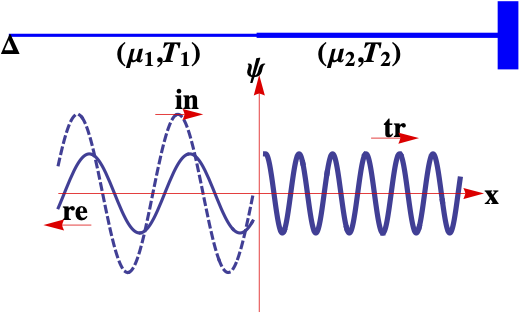
Suppose the vibrator is vibrating at a particular (angular) frequency \(\omega\text{.}\) Then, the frequencies of three waves, incident, reflected, and transmitted, will all be same as \(\omega\text{.}\) However, two of these waves, viz., incident and reflected, move in the medium of wave speed \(v_1 = \sqrt{T/\mu_1}\text{,}\) therefore, they will have the same wavenumber and same wavelength. But, the transmitted wave moves in a medium of wave speed \(v_2 = \sqrt{T/\mu_2}\text{,}\) which is different than \(v_1\text{.}\) As a result, the transmitted wave will have different wavenumber and wavelength. Using \(k=\omega/v\) relation of waves we have the following.
\begin{align*}
\amp k_1= \omega/v_1 = \omega\sqrt{\mu_1/T},\\
\amp k_2= \omega/v_2 = \omega\sqrt{\mu_2/T}.
\end{align*}
Since wave number \(k\) of a wave is related to wavelength \(\lambda\) by \(k = 2\pi/\lambda\text{,}\) this says that the wavelengths of a wave of same frequency will be different in the two media. Let \(\lambda_1\) and \(\lambda_2\) for the respective wavelengths, then we have
\begin{equation*}
\frac{\lambda_1}{v_1} = \frac{\lambda_2}{v_2} = \frac{2\pi}{\omega} = \dfrac{1}{f},
\end{equation*}
where \(f\) is the regular frequency, common to all three waves.
Subsection 14.12.1 (Calculus) Boundary Conditions
Suppose the two strings in Figure 14.40 are semi-infinite in extent, that is, we assume the vibrator and the post are far away from the knot at \(x=0\text{.}\) Suppose the strings are tied together smoothly and the knot be considered massless. Let \(\psi_1(x,t)\) be the transverse displacement of the string on the left of \(x=0\text{,}\) i.e. when \(x \lt 0\text{,}\) and \(\psi_2(x,t)\) be the transverse displacement on the right of \(x=0\text{,}\) i.e. when \(x \gt 0\text{,}\) respectively. Here \(\psi_1\) will be a sum of incident and reflected waves and \(\psi_2\) will just be the transmitted wave.
Since the strings are continuous at the junction the displacement of the string at the boundary at \(x=0\) must be same whether we use \(\psi_1\) or \(\psi_2\) for the displacement at that point. Furthermore, the force on the know should be balanced. These two requirements give us boundary conditions relating \(\psi_1\) and \(\psi_2\text{.}\)
\begin{gather}
\psi_1(0,t) = \psi_2(0,t)\tag{14.81}\\
\left( \dfrac{\partial\psi_1(x,t)}{\partial x} \right)_{x=0}= \left( \dfrac{\partial\psi_2(x,t)}{\partial x} \right)_{x=0}\tag{14.82}
\end{gather}
Subsection 14.12.2 Reflection and Transmission Amplitudes
We now apply boundary conditions, Eqs. (14.81) and (14.82), to the situation of waves on the string in Figure 14.40. First we need analytic representations of the three waves. Let incident wave be a sinusidal wave of amplitude \(A_\text{in}\) with the following expression.
\begin{equation*}
\psi_\text{in} = A_\text{in}\cos(k_1 x - \omega t).
\end{equation*}
The reflected wave will be moving to the left. Let its amplitude be denoted by \(A_\text{re}\text{,}\) which can be negative if wave flips over upon reflection.
\begin{equation*}
\psi_\text{re} = A_\text{re}\cos(k_1 x + \omega t).
\end{equation*}
Note the signs of the two terms in the argument of cosine is same since this wave is traveling towards negative \(x\) axis. Finally, let us denote the amplitude of the transmitted wave by \(A_\text{tr}\text{.}\)
\begin{equation*}
\psi_\text{tr} = A_\text{tr}\cos(k_2 x - \omega t).
\end{equation*}
Now, we note that the net wave on the left, \(\psi_1\text{,}\) is superposition of \(\psi_\text{in}\) and \(\psi_\text{re}\text{,}\) but \(\psi_2\) is just the tranmitted wave.
\begin{align}
\amp \psi_1 = A_\text{in}\cos(k_1 x - \omega t) + A_\text{re}\cos(k_1 x + \omega t), \tag{14.83}\\
\amp \psi_2 = A_\text{tr}\cos(k_2 x - \omega t).\tag{14.84}
\end{align}
When, we apply two boundary conditions, given in Eqs. (14.81) and (14.82), at \(x=0\text{,}\) we find reflection and transmission amplitudes in terms of the incident amplitude. Let us define these ratios, called reflection and transmission coefficients for simplifying the expressions later. Let
\begin{equation*}
\rho = \frac{A_\text{re}}{A_\text{in}},\ \ \ \tau = \frac{A_\text{tr}}{A_\text{in}}.
\end{equation*}
The boundary conditions give us the following equations.
\begin{align}
\amp 1 + \rho = \tau,\tag{14.85}\\
\amp -k_1 + k_1 \rho = k_2 \tau.\tag{14.86}
\end{align}
These can be solved for refelction and transmission coefficients.
\begin{align}
\amp \rho = \frac{k_1 - k_2}{k_1 + k_2},\tag{14.87}\\
\amp \tau = \frac{2k_1}{k_1 + k_2}.\tag{14.88}
\end{align}
Of coourse, we can express them in terms of wavelengths and speeds as well.
\begin{align}
\amp \rho = \frac{\lambda_2 - \lambda_1}{\lambda_2 + \lambda_2} = \frac{v_2 - v_1}{v_2 + v_2},\tag{14.89}\\
\amp \tau = \frac{2v_2}{v_2 + v_2}.\tag{14.90}
\end{align}
We see that, when \(\mu_2 \gt \mu_1\text{,}\) corresponding to \(v_2 \lt v_1\text{,}\) or alternately \(\lambda_2 \lt \lambda_1\text{,}\) the reflection coefficient is negative. Negative reflection coefficient means the reflecion displacement is opposite to the incident displacement, i.e., the reflected wave is inverted relative to the incident wave as shown in Figure 14.40. The transmitted wave is always positive, meaning, it is not inverted in relation to the incident wave.
Reflection and transmission coefficients, given in Eqs. (14.87) to (14.90) are often written in terms of another property of medium called impedance and denoted by letter \(Z\text{.}\) Impedance of string of tension \(T\) and mass per unit length \(\mu\) is defined by
\begin{equation}
Z = \sqrt{T\mu}.\tag{14.91}
\end{equation}
This is also ratio of tension \(T\) and speed \(v\) of the wave.
\begin{equation}
Z = \frac{T}{v}.\tag{14.92}
\end{equation}
In terms of \(Z_1\) and \(Z_2\) of the two media, the reflection and transmission coefficients are
\begin{align}
\amp \rho = \frac{Z_1 - Z_2}{Z_1 + Z_2},\tag{14.93}\\
\amp \tau = \frac{2Z_1}{Z_1 + Z_2}.\tag{14.94}
\end{align}
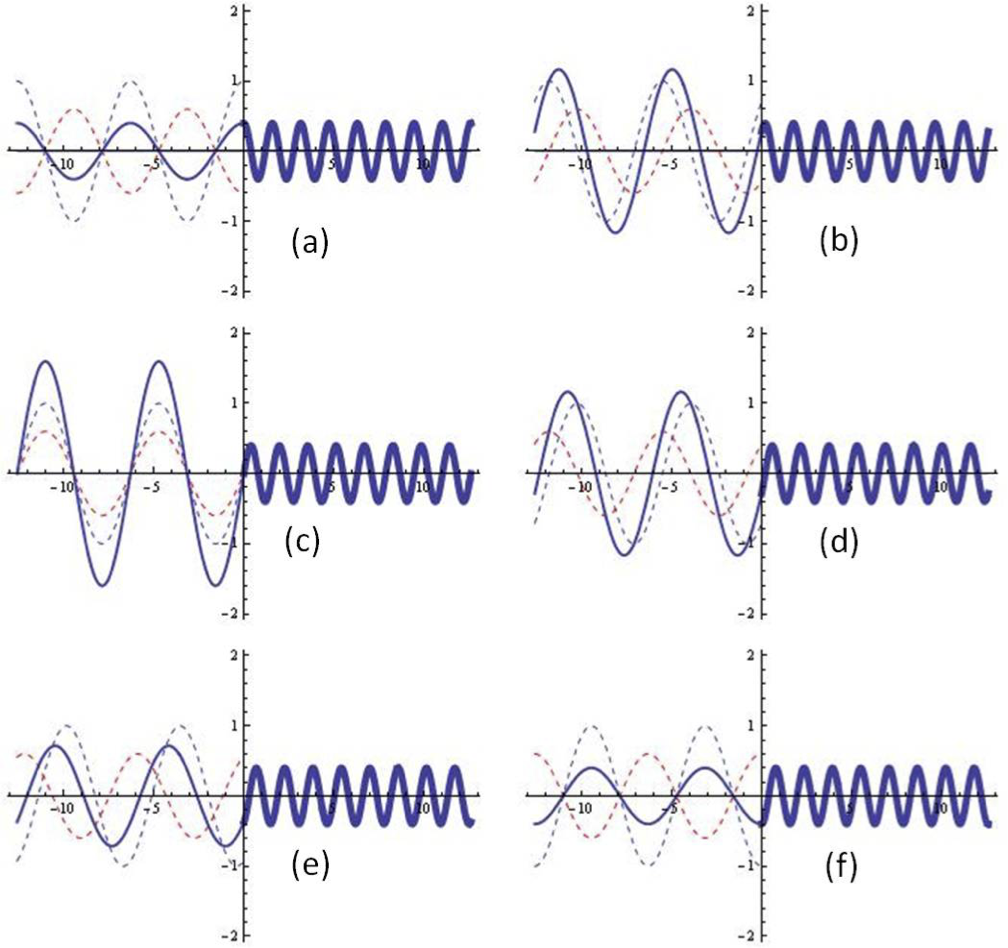
Figure 14.41 shows reflection and transmission in case of \(Z_2 \gt Z_1\) at different times to show how incident wave reflecs and combines with the reflected wave.
Subsection 14.12.3 Perfect Reflection
Suppose, instead of tying the left string to the right string, it is tied to a fixed support. That is, we have one string which is being vibrated at some point, say, \(x=-\infty\text{,}\) and a wave is being sent down the string towards the positive \(x\)-axis, and let the string be attached to the fixed support at \(x=0\text{.}\) We can think of the fixed support as if the second string in the example above having an infinite mass density, making \(Z_2 = \infty\text{.}\) Therefore, the large \(Z_2\) limit of Eqs. (14.93) and (14.94) will give us reflection from a massive string or a fixed post.
\begin{gather}
\hskip-1.5cm\text{Reflection from fixed end:}\notag\\
\rho = \lim_{Z_2 \to \infty}\frac{Z_1-Z_2}{Z_1+Z_2} = -1,\tag{14.95}\\
\tau=\lim_{Z_2 \to \infty}\frac{2Z_1}{Z_1+Z_2}=0.\tag{14.96}
\end{gather}
That is, the wave will be fully reflected with the same amplitude as the incident wave but of opposite phase and there will be no transmission for reflection from a fixed post. The right-moving wave and the left moving wave add up to give a standing wave on the string.
\begin{equation*}
A\cos(kx-\omega t) + (-1)A\cos(kx+\omega t) \rightarrow 2 A \sin(kx) \sin(\omega t).
\end{equation*}
Subsection 14.12.4 Perfect Termination and Impedance Matching
From Eq. (14.93) we find that if impedance of the second medium is equal to the impedance of the first medium, i.e., when the impedances are matched, the reflection coefficient will be zero.
\begin{equation*}
\rho = 0\ \ \text{when}\ \ Z_1 = Z_2.
\end{equation*}
That is, the first string will not experience a recoil force and the wave will seamlessly enter the second string as if the boundary was not there. In this case the length of the second string does not matter since the second string just moves with the first string as the incident wave arrives at the junction. We say that the second string is a perfect terminator of the wave.

