Planar Sound Wave

Section 15.2 Planar Sound Wave

Consider a planar sound wave in air of frequency $f$ and wavelength $\lambda\text{.}$ We can think of this wave in terms of displacement of particles of the air or in terms of presser differences at different places. Let us first look at the displacement wave.

🔗

Let direction of wave be towards the positive $x$ axis and amplitude of the wave at the origin be $0$ at $x=0$ and $t=0\text{.}$ Then displacement at $x$ at intant $t$ will be give by

\begin{equation} \psi(x,t) = D_0 \sin\left( \frac{2\pi}{\lambda} x - 2\pi f t\right),\tag{15.4} \end{equation}

where $D_0$ is the amplitude of the wave. We use letter $D$ for the amplitude instead of $A$ because we will use $A$ for area below. The wavenumber $k$ and angular frequency $\omega$ of the wave are

\begin{equation*} k = \frac{2\pi}{\lambda},\ \ \omega = 2\pi f. \end{equation*}

🔗

To obtain the corresponding pressure wave, we need to look at a small volume through which this displacment wave is passing and apply the definition of Bulk modulus $B$ from the chapter on Statics. The pressure change $\Delta P$ for a fractional volume change $\Delta V / V$ is related by Bulk modulus $B$ by

\begin{equation*} \Delta P = - B\frac{\Delta V}{V}. \end{equation*}

🔗

Consider a small box of thickness $\Delta x$ along the wave and area $A$ perpendicular to the wave. Suppose as a result of the displacement wave $\psi\text{,}$ this box is shrunk by $\Delta \psi\text{.}$ this shrinking will happen due to different values of $\psi$ at the two ends of the box separated by $\Delta x\text{.}$

🔗

Thus, volume change will be $\Delta V = A\Delta \psi$ while the original volume was $A\Delta x\text{.}$ From the definition of bulk modulus in chapter on statics, you will note that the pressure in the box will change by $\Delta P$ given by

\begin{equation*} \Delta P = - B\frac{\Delta \psi}{\Delta x}. \end{equation*}

🔗

In the limit of $\Delta x \rightarrow 0$ this becomes a partial derivative with respect to $x\text{.}$

\begin{equation} \Delta P = - B\frac{\partial \psi}{\partial x}.\tag{15.5} \end{equation}

Using $\psi$ from Eq. (15.4) we get

\begin{equation} \Delta P = - \frac{2\pi}{\lambda} D_0 B \cos\left( \frac{2\pi}{\lambda} x - 2\pi f t\right).\tag{15.6} \end{equation}

We can write this as a sine function to compare with the displacement wave as

\begin{equation} \Delta P = P_0 \sin\left( \frac{2\pi}{\lambda} x - 2\pi f t - \frac{\pi}{2}\right),\tag{15.7} \end{equation}

where $P_0$ is the amplitude of the pressure wave

\begin{equation*} P_0 = \frac{2\pi}{\lambda} D_0 B. \end{equation*}

Note that the argument of sine for pressure wave has a phase constant of $-\pi/2$ as compared to the displacement wave give in Eq. (15.4). Thus, pressure wave has peaks and troughs when displacement wave is zero and vice versa as shown in Figure 15.4. Also, notice that pressure and displacement waves have same frequency, wavelength and wave speed.

🔗

Figure 15.4. Comparison of displacement wave $\psi$ (the solid line) and pressure wave $\Delta P$ (the dashed line) in space at one instant.
🔗

Exercises Exercises

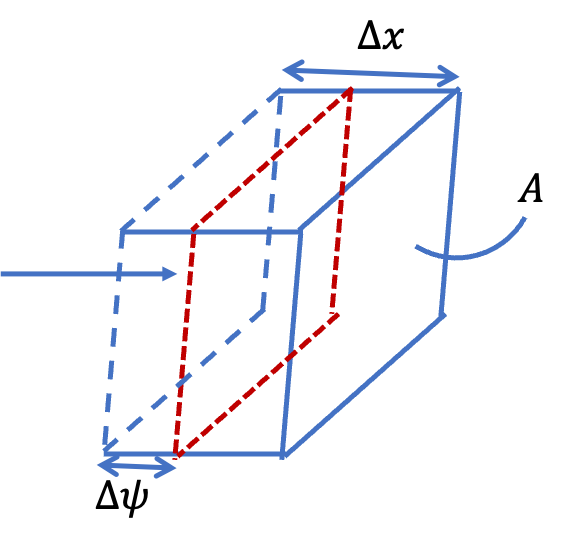
1. Obtaining Properties of Sinusoidal Waves from Wave Function.

The sound produced by a speaker is given by the following pressure difference wave in air.

\begin{equation*} \Delta p = (10 \text{ Pa})\, \cos(k x + 6000\, t + \pi), \end{equation*}

where $x$ is in meters and $t$ in seconds and $\Delta p(x,t)$ is the difference in atmospheric pressure from the ambient pressure at location $x$ at time $t\text{.}$ Suppose speed of this wave is $343\text{ m/s}$ and density of air to be $1.2\, \text{kg/m}^3\text{.}$

🔗

(a) Angular frequency,

🔗

(b) Frequency,

🔗

(d) Amplitude of the wave,

🔗

(e) The direction the wave is traveling,

🔗

(f) Bulk modulus of air,

🔗

(g) Pressure differential at $x=0$ at $t=0\text{,}$

🔗

(h) Pressure at $x=0$ at $t=0\text{,}$

🔗

(i) Pressure differential at $x=0\text{,}$ $t = 1/5000$ sec,

🔗

(j) Plot the pressure differential at $x=0$ versus $t\text{,}$

🔗

(k) Plot the pressure differential at $t=0$ versus $x\text{.}$

🔗

(l) What is the corresponding particle displacement wave?

🔗

Hint.

The $\Delta p$ is just a sinusoidal wave.

🔗

Answer.

(b) 955 Hz; (c) 35.9 m; (e) negative x-axis; (g) -10 Pa; (l) $(4\ \mu\text{m})\cos(17.5 x+ 6000 t + 3\pi/2)$

🔗

Solution 1. a-k

Angular frequency, $\omega = 6000\, \text{rad/s}\text{.}$
🔗

🔗
Frequency, $f = \omega/2\pi = 955\, \text{Hz}\text{.}$
🔗

🔗
Wavelength, $\lambda = v/f = 343 / 955 = 0.359\,\text{m}\text{.}$
🔗

Wavenumber, $k = \frac{2\pi}{\lambda} = 17.5\,\text{m}^{-1}\text{.}$
🔗

🔗
Amplitude of the wave, $A = 10\,\text{Pa}\text{.}$
🔗

🔗
The direction the wave is traveling: Negative $x$-axis since the $x$ and $t$ terms in the argument have the same sign.
🔗

🔗
Bulk modulus of air $B$ is obtained from $v = \sqrt{B/\rho}$ with $\rho$ the density of air. This gives $B = \rho v^2 = 0.14\, \text{MPa}\text{.}$
🔗

🔗
Pressure differential at $x=0$ at $t=0\text{:}$ $\Delta p = - 10\, \text{Pa}\text{.}$
🔗

🔗
Pressure at $x=0$ at $t=0\text{:}$ $P = 1$ atm $-10$ Pa.
🔗

🔗
Pressure differential at $x=0\text{,}$ $t = 1/5000$ sec: $\Delta p = - 3.63\,\text{Pa}\text{.}$
🔗

🔗
Plot the pressure differential at $x=0$ versus $t\text{:}$ left as an exercise for student to complete.
🔗

🔗
Plot the pressure differential at $t=0$ versus $x\text{:}$ left as an exercise for student to complete.
🔗

🔗

🔗

Solution 2. l

The phase of the dsplacment will have additional $+\pi/2$ constant and the amplitude will be

\begin{equation*} D_0 = \frac{P_0}{k B} = 4.1\times 10^{-6}\,\text{m} = 4.1\,\mu\text{m}. \end{equation*}

Hence, the particle displacement wave with this sound wave is $(4\ \mu\text{m})\cos(17.5 x+ 6000 t + 3\pi/2)\text{.}$

🔗

2. Properties of Particle Displacement Wave.

The sound produced in air by a speaker is given by the following displacement wave function.

\begin{equation*} \psi(x,t) = (100\ \mu m)\cos(120 x + \omega t + \pi/2), \end{equation*}

where $t$ is in seconds, $x$ in meters and $\psi$ in micrometers. Assume the speed of sound in air to be 343 m/s and the density of air to be $1.2$ kg/m$^3$. Find the following.

🔗

Wavelength and wavenumber,

🔗

Frequency and Angular frequency,

🔗

Angular frequency,

🔗

Amplitude of the displacement wave,

🔗

The direction the wave is traveling in,

🔗

Displacement of particles at $x=0$ at $t=0$,