Moment of Inertia

Section 9.7 Moment of Inertia

We found above that angular momentum of a body rotating with angular velocity \(\omega \) about a principal axis is

\begin{equation*} L = I\,\omega, \end{equation*}

where \(I \) is the moment of inertia of the body about the axis of rotation. If you compare this formula with the formula for the magnitude of momentum of a particle of mass \(m \) and velocity \(\vec v \text{.}\)

\begin{equation*} p = m v, \end{equation*}

you will notice that moment of inertia \(I \) plays the same role in rotation as mass \(m \) plays in the translational motion.

When we studied \(\vec F = m\vec a \) for constant mass system, we found that mass \(m\) can be interpreted as a measure of inertia against change in velocity. Later in this chapter, when we introduce a similar dynamic equation, \(\tau = I \alpha\) for constant \(I\) system, where \(\tau\) is torque of the force, we will find that \(I \) is a measure of inertia against change in angular velocity, and hence the name, moment of inertia.

In this section, we will practice computing moment of inertia of some commonly encountered objects, starting from the fundamental formula for the moment of inertia of a single particle.

Subsection 9.7.1 Moment of Inertia of Single Particle

Consider a single particle of mass \(m\) moving in a circle of radius \(R\) as shown in Figure 9.55. We can think of it as a particle rotating about an axis at a distance \(R \) from the axis. The moment of inertia of this system is

\begin{equation} I_{\text{particle}} = m\,R^2.\tag{9.31} \end{equation}

This will be the building block for moment of inertia of an arbitrary object.

Subsection 9.7.2 Moment of Inertia of Systems of Particles

Suppose we have \(N\) particles that rotate about a common axis as shown in Figure 9.56. The figure shows a system of 4 particles. Let \(m_1\text{,}\) \(m_2\text{,}\) \(\cdots\text{,}\) be their masses and \(R_1\text{,}\) \(R_2\text{,}\) \(\cdots\text{,}\) be their distances from the axis. The net moment of inertia will be the sum of moment of inertia for each particle.

\begin{equation} I_{N\text{-particles}} = m_1 R_1^2 + m_2 R_2^2 + \cdots + m_N R_N^2.\tag{9.32} \end{equation}

We might write this using a sum notation.

\begin{equation} I_{N\text{-particles}} = \sum_{i=1}^{N}m_i R_i^2 .\tag{9.33} \end{equation}

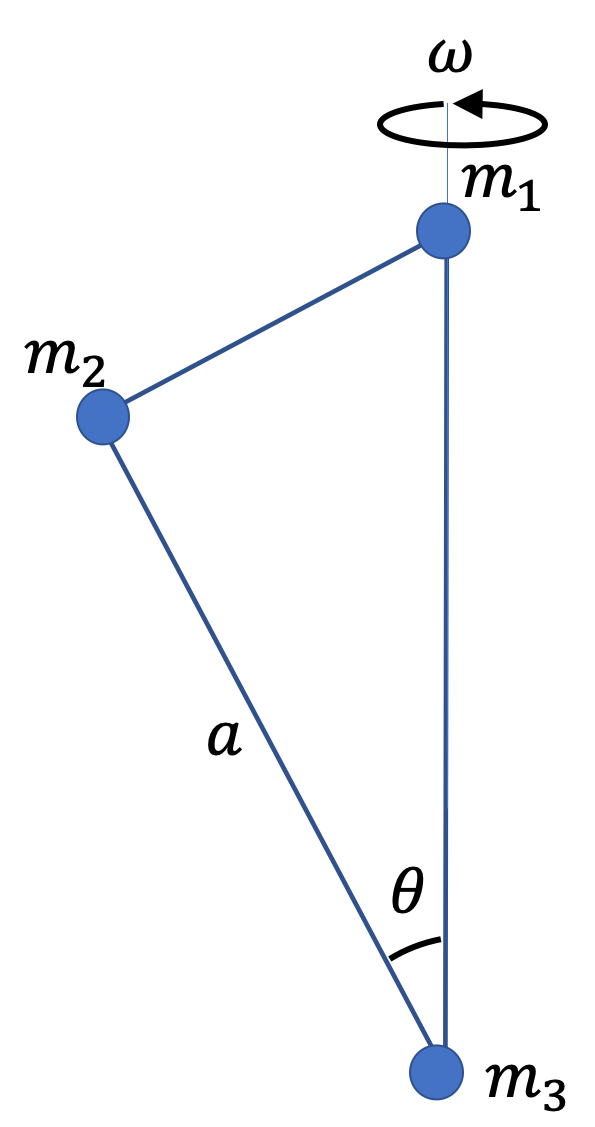
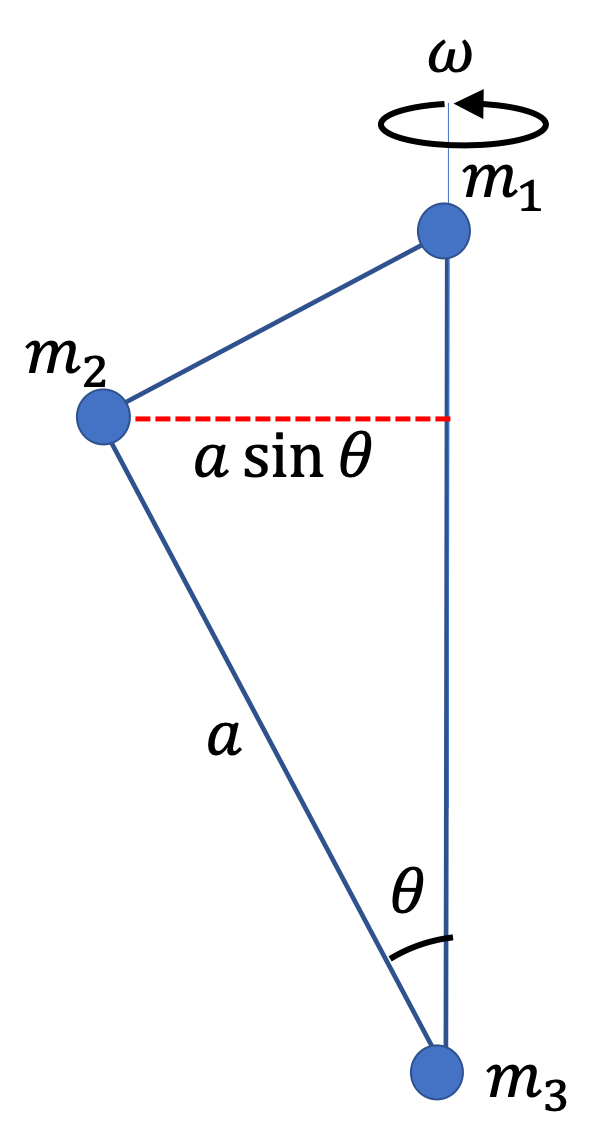
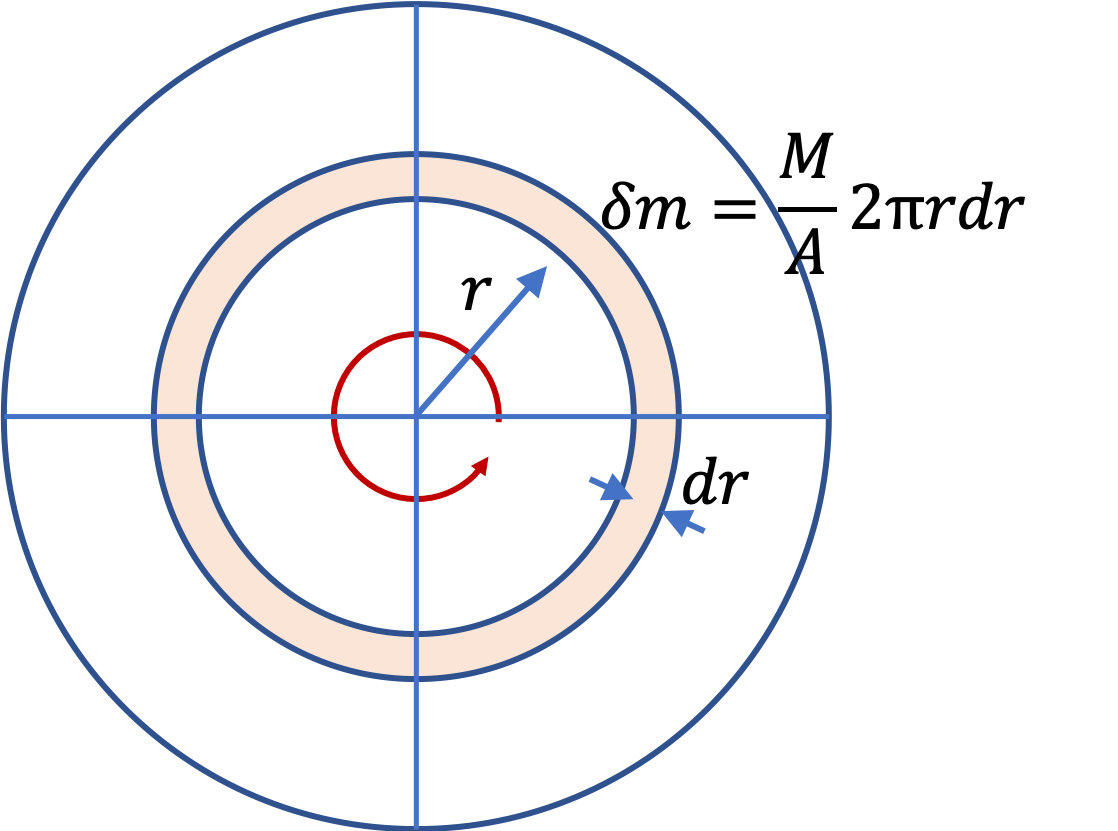
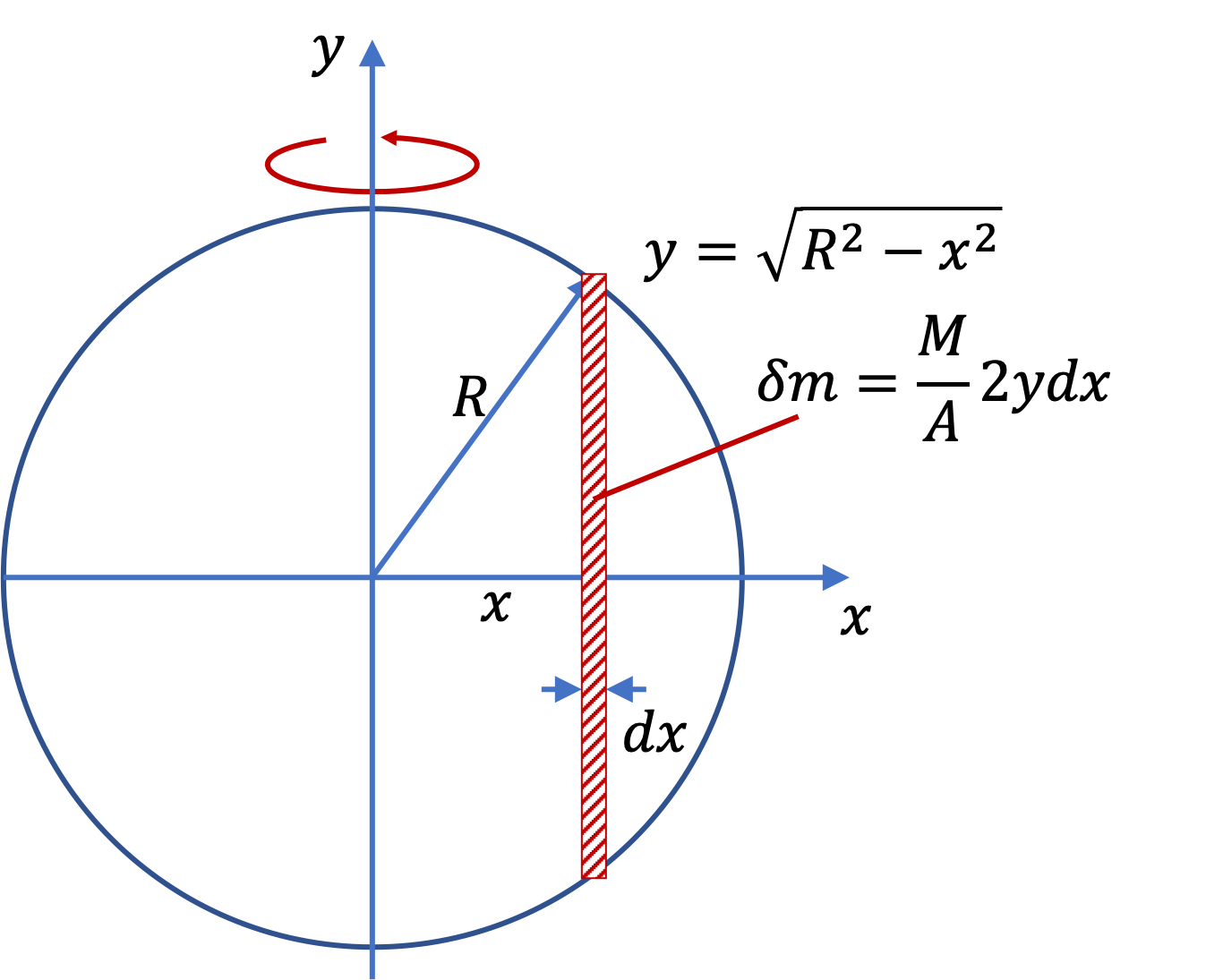
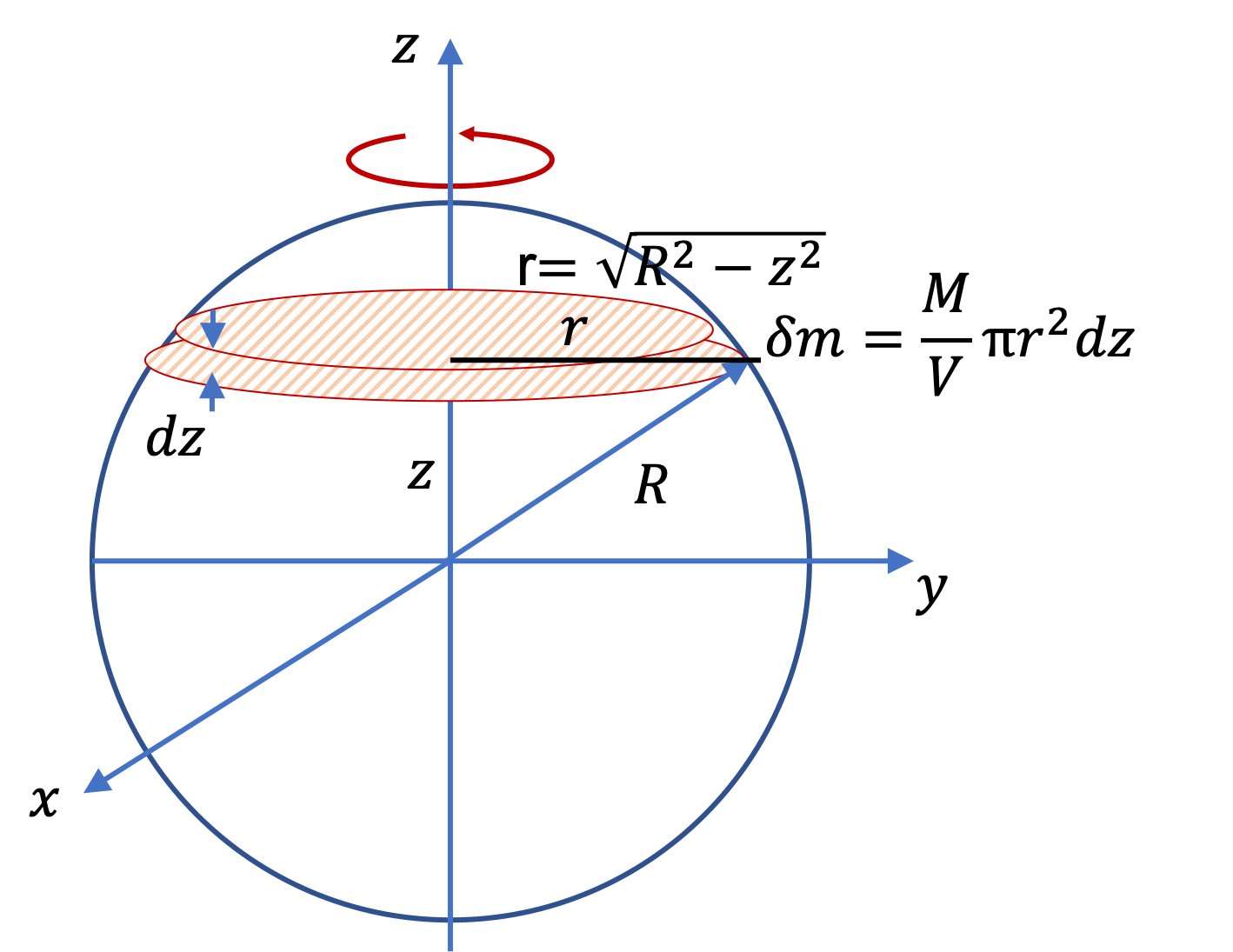
Example 9.57. Moment of Inertia of a Baton about an Irregular Axis.

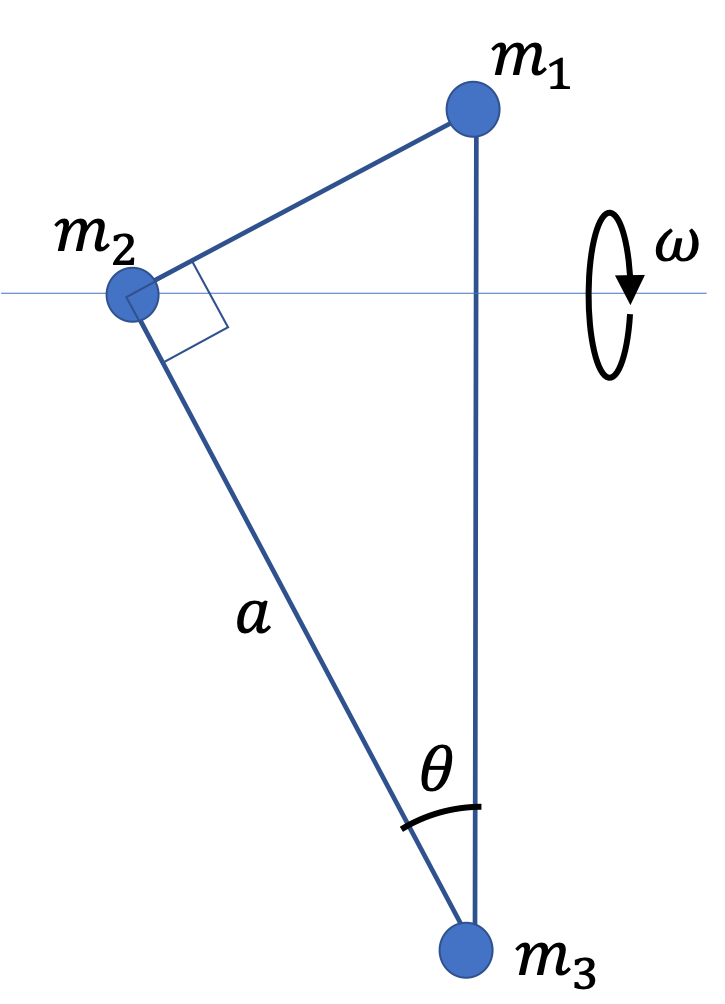
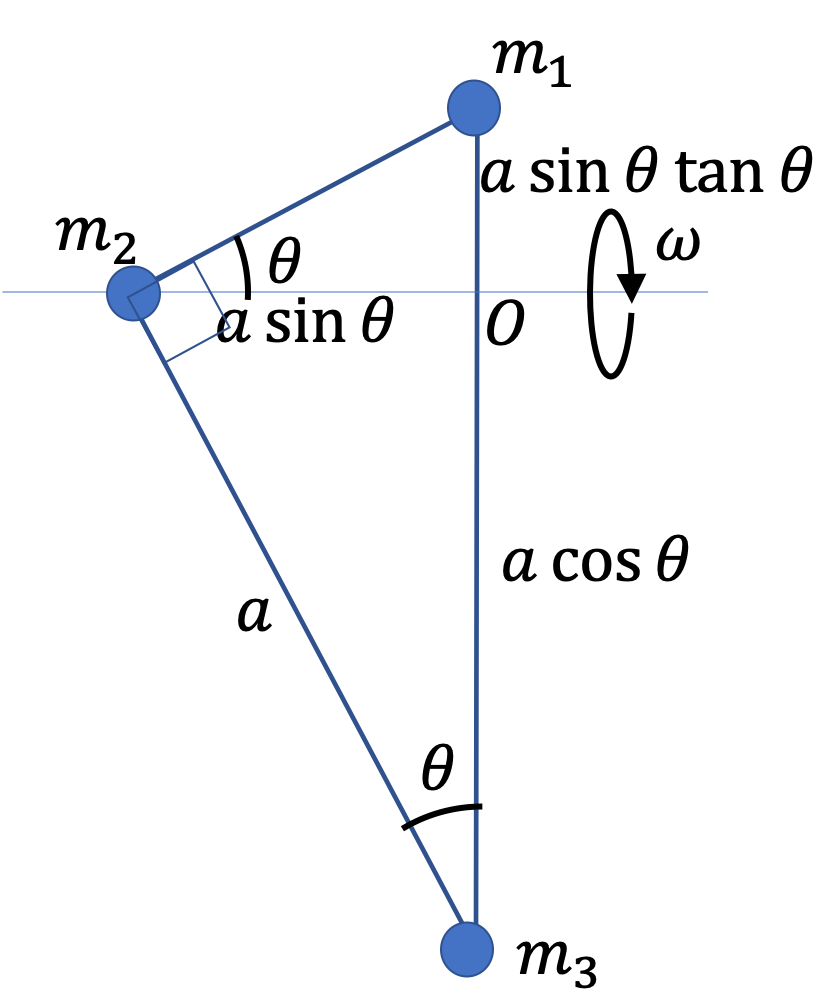
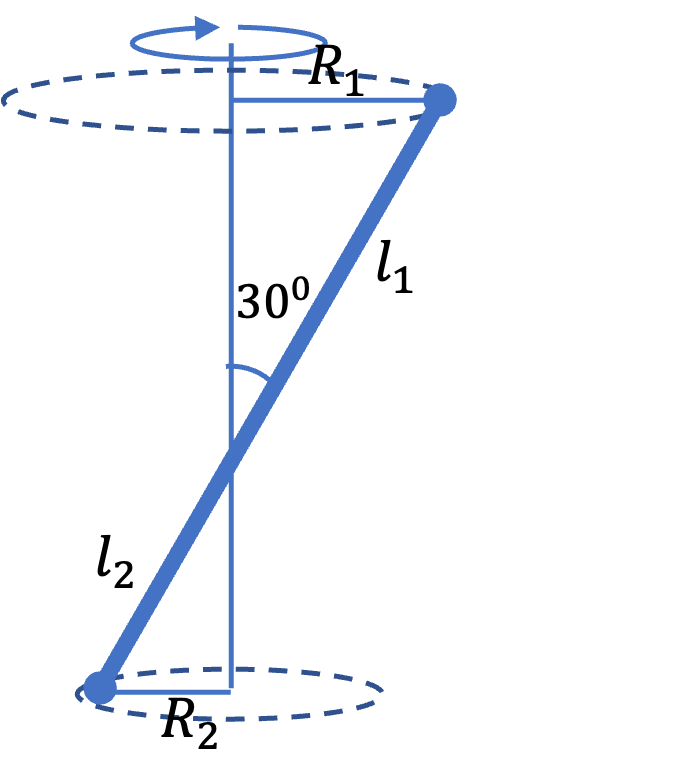
A \(1.2\text{-m}\) baton has a \(0.4\text{-kg}\) ball at each end. The rod of the baton has considerably smaller mass which we can ignore in this problem. The baton is held at \(0.5\text{ m}\) from one end and twirled so that the two masses rotate about a vertical axis at an angle of \(30^{\circ}\) from the axis.

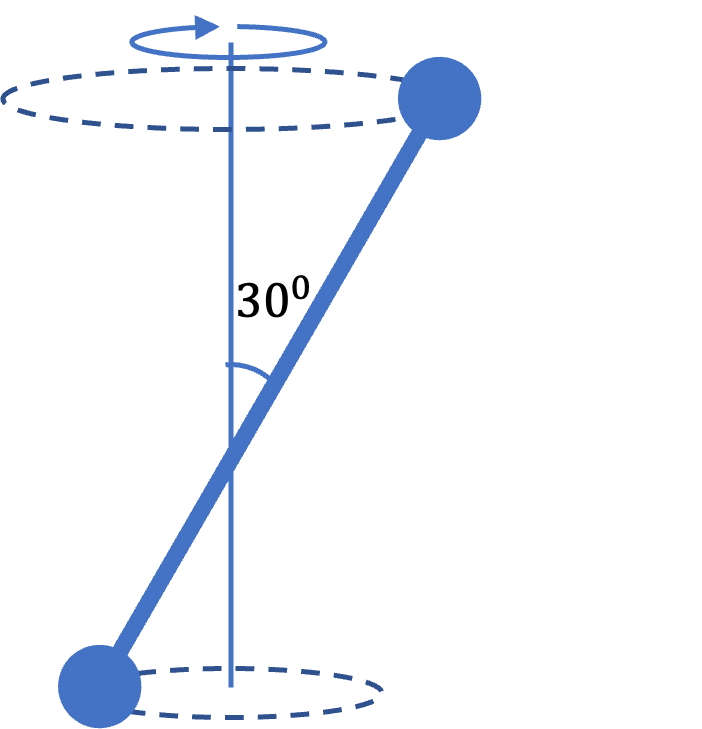
(a) Find the distances of the two masses from the axis of rotation.

(b) Find the moment of inertia of the baton about the axis described in the problem.

Answer.

(a) \(0.35\text{ m}\text{,}\) \(0.25\text{ m}\) (b) \(0.074\text{ kg.m}^2 \text{.}\)

Solution 1. a

We figure out the distances from the radii of the circles in which the balls move. We do that by dropping a perpendicular from the masses to the axis and using trig on the triangle formed.

\begin{align*} \amp R_1 = l_1\,\sin\,30^{\circ} = \dfrac{0.7}{2} = 0.35\text{ m}. \\ \amp R_2 = l_2\,\sin\,30^{\circ} = \dfrac{0.5}{2} = 0.25\text{ m}. \end{align*}

Solution 2. b

From the masses and the distances from the axis, we get

\begin{equation*} I = m_1 R_1^2 + m_2 R_2^2 = 0.4\times(0.35^2 + 0.25^2) = 0.074\text{ kg.m}^2. \end{equation*}

Example 9.60. Moment of Inertia and Angular Momentum of a Three Particle System.

Three particles of masses \(m_1\text{,}\) \(m_2\text{,}\) and \(m_3\) are rotating with angular speed \(\omega\) about the given axis shown in Figure 9.61. Find the magnitude and direction of the total angular momentum in two different ways: (a) from a sum of the angular momentum of each particle, and (b) first finding the moment of inertia of the three as a system about the axis of rotation, and then multiplying the moment of inertia about the axis with the angular velocity about that axis.

Answer.

(a) \(m_2\, \omega\, a^2\,\sin^2\theta\text{,}\) up. (b) Same as (a).

Solution 1. a

Each particle has angular momentum \(l = mvr\) where \(r\) is the radius of its circle of motion. Speed of its motion will be \(v = \omega r \text{.}\) Therefore, we will get

\begin{align*} \amp l_1 = 0,\ \text{ since } r_1 = 0.\\ \amp l_2 = m_2\, \left( \omega\, a\,\sin\theta \right)\, a\,\sin\theta ,\ \text{ since } r_2 = a\,\sin\theta.\\ \amp l_3 = 0,\ \text{ since } r_3 = 0. \end{align*}

Using the right-hand rule, we get the direction of \(\vec l_2\) to be up. Therefore, the total angular momentum is \(m_2\, \omega\, a^2\,\sin^2\theta\text{,}\) pointed up.

Solution 2. b

The moment of inertia of a point particle is \(mr^2\) where \(r\) is the radius of its circle of motion. From the radii found in (a), we can immediately write the moment of inertia to be

\begin{equation*} I = 0 + m_2\, a^2\,\sin^2\theta + 0. \end{equation*}

Therefore, the magnitude of angular momentum will be \(I\omega\text{,}\) which is the same as we found in (a). The direction is found by applying the right-hand rule, which gives the direction up.

Example 9.63. Moment of Inertia and Angular Momentum of a Three Particle System Different Axis.

Three particles of masses \(m_1\text{,}\) \(m_2\text{,}\) and \(m_3\) are rotating with angular speed \(\omega\) about the given axis shown in the figure. Find the magnitude and direction of the total angular momentum in two different ways: (a) from a sum of the angular momentum of each particle, and (b) first finding the moment of inertia of the three as a system about the axis of rotation, and then multiplying the moment of inertia about the axis with the angular velocity about that axis.

Answer.

(a) \(\frac{\omega\, a^2}{\cos^2\theta}\, \left( m_1\, \sin^4\theta + m_3\,\cos^4\theta \right)\text{,}\) to the right. (b) Same as (a).

Solution 1. a

First, we figure out the radii of the circles of the motion of each particle. The figure is helpful in that.

\begin{align*} \amp r_1 = a\,\sin^2\,\theta/\cos\,\theta,\\ \amp l=r_2 = 0,\\ \amp r_3 = a\,\cos\,\theta. \end{align*}

Each particle has angular momentum \(l = mvr\) where \(r\) is the radius of its circle of motion. Speed of its motion will be \(v = \omega r \text{,}\) where \(\omega\) is same for all particles.

Therefore, we will get

\begin{align*} \amp l_1 = m_1\,\omega\, \left( a\,\sin^2\,\theta/\cos\,\theta \right)^2,\\ \amp l_2 = 0,\\ \amp l_3 = m_3\,\omega\, \left( a\,\cos\,\theta \right)^2. \end{align*}

Both \(l_1\) and \(l_3\) are pointed in the same direction, to the direction right. Therefore, they will add, giving us the magntitude of the net angular momentum to be

\begin{equation*} L = \omega\, a^2\, \left( m_1\, \sin^4\theta/\cos^2\theta + m_3\,\cos^2\theta \right). \end{equation*}

Solution 2. b

The moment of inertia of a point particle is \(mr^2\) where \(r\) is the radius of its circle of motion. From the radii found in (a), we can immediately write the moment of inertia to be

\begin{equation*} I = m_1\, a^2\,\sin^4\theta/\cos^2\theta + 0 + m_3\,a^2\,\cos^2\theta. \end{equation*}

Therefore, the magnitude of angular momentum will be \(I\omega\text{,}\) which is the same as we found in (a). The direction is found by applying the right-hand rule, which gives the direction right.

Subsection 9.7.3 Moment of Inertia of a Uniform Rod

We look at the simplest continuous mass system - a rod of length \(L\) and mass \(M\text{,}\) rotating about an axis that passes through one edge perpendicular to the rod as shown in the figure.

If we divide up the rod into \(N \) parts, we can essentially turn the rod into \(N\)-particle system as shown in Figure 9.66.

Figure 9.66. We divide up the rod into \(N\) (shown 7) equal cells and place the masses in each piece at one end of each cell. We can then use the formula for the moment of inertia of each mass to estimate the moment of inertia of the rod.

For simplicity, let us take the segments to be of equal length \(\Delta r\text{,}\)

\begin{equation*} \Delta r = \dfrac{L}{N}. \end{equation*}

We now place the masses in each segment at the right end of the segments. This gives us the distance \(R_i\) to the \(i\)-th mass as follows,

\begin{equation*} R_i = i\Delta r, \end{equation*}

with mass in each segment

\begin{equation*} m_i = \dfrac{M}{N}. \end{equation*}

This will result in the following formula for the moment of inertia.

\begin{equation*} I = \sum_{i=}^{N}m_i R_i^2 = \dfrac{M (\Delta r)^2 }{N}\sum_{i=1}^{N}\, i^2. \end{equation*}

The sum the squares of integers is known to be

\begin{equation*} \sum_{i=1}^{N}\, i^2 = \dfrac{N (N + 1) (2N + 1)}{6}. \end{equation*}

Therefore, dividing up the rod in \(N\) equal parts gives us the following formula for the moment of inertia of the rod.

\begin{equation*} I = \dfrac{M (\Delta r)^2 }{N} \times \dfrac{N (N + 1) (2N + 1)}{6}. \end{equation*}

Cancelling \(N \) from numerator and denominator simplifies this to

\begin{equation*} I = \dfrac{1}{6}\, M (\Delta r)^2 (N + 1) (2N + 1). \end{equation*}

Now, the original rod had many particles; in an ordinary sized rod, \(N \) would be of the order of Avogadro number, \(N_A = 6 \times 10^{23}\text{.}\) That will make adding 1 to \(N \) or to \(2N\) insignificant. Thus,

\begin{equation*} I = \dfrac{1}{6}\, M (\Delta r)^2 \times 2N^2 = \dfrac{1}{3} M (N\Delta r)^2. \end{equation*}

Using \(N\Delta r = L\text{,}\) the length of the rod, we finally get the formula for moment inertia of a rod about an axis through one end.

\begin{equation} I_{\text{rod}}^{\text{axis-at-end}} = \dfrac{1}{3}\, M L^2.\tag{9.34} \end{equation}

Example 9.67. A Chain of Rings Rotating About an Axis Through One End.

N rings, each of mass \(m\text{,}\) are linked together into a chain and hung from the middle. The chain is then rotated at an angular speed of \(\omega\) such that the angle with the vertical is \(\theta\) as shown in the figure. Model the chain as a sequence of masses separated by distance \(a \text{,}\) and find the magnitude and direction of angular momentum.

Hint.

Use \(L=I\omega\text{.}\) Find \(I\) by adding up the \(I\) of each ring. You may fin dit helpful to focus on an arbitrary \(i\)-th ring.

Answer.

\(\left( m a^2 \sin^2\theta\right)\, \dfrac{N(N+1)(2N+1)}{6}\, \omega\text{,}\) in direction up.

Solution.

Let \(r_i\) be the radius of the circle in which the \(i\)-th ring rotates. The distance of this ring from the support is \(ia\text{.}\) Therefore, the moment of inertia of this ring is

\begin{equation*} I_i = mr_i^2 = m \left( i a \sin\,\theta\right)^2 = \left( m a^2 \sin^2\theta\right)\, i^2. \end{equation*}

Summing these for all \(N\) rings gives

\begin{align*} I \amp = \sum I_i = \left( m a^2 \sin^2\theta\right)\, \sum_{i=1}^{N} i^2 \\ \amp = \left( m a^2 \sin^2\theta\right)\, \dfrac{N(N+1)(2N+1)}{6}. \end{align*}

Therefore, the magnitude of angular momentum will be

\begin{equation*} L = I\omega = \left( m a^2 \sin^2\theta\right)\, \dfrac{N(N+1)(2N+1)}{6}\, \omega. \end{equation*}

By using the right-hand rule, the direction of \(\vec L\) is up.

Subsection 9.7.4 The Parallel-Axis Theorem

The parallel-axis theorem establishes a relation between the moment of inertia about an axis through the center of mass and about another axis that is parallel to this axis. We will state it here and prove in the Calculus-based section.

Let \(M\) be the mass of the object, \(I_{\text{cm}}\) be the moment of inertia about an axis through the center of mass and \(I_{\text{A}}\) be the moment of inertia about a parallel axis that is a distance \(d\) away. Then,

\begin{equation} I_{\text{A}} = I_{\text{cm}} + M\,d^2.\tag{9.35} \end{equation}

Example 9.70. Moment of Inertia Through the CM of a Rod.

The moment of inertial of a rod of length \(L \) and mass \(M\) about an axis through one edge and perpendicular to the rod is given by

\begin{equation*} I_{\text{edge}} = \dfrac{1}{3}ML^2. \end{equation*}

Find the moment of inertia of the rod about an axis through the center of the rod and perpendicular to the rod.

Answer.

\(\dfrac{1}{12}ML^2\text{.}\)

Solution.

Using the parallel axis theorem, we can write the following relation.

\begin{equation*} I_{\text{edge}} = I_{\text{cm}} + M\,\left( \dfrac{L}{2} \right)^2 \end{equation*}

Using the formula, \(I_{\text{edge}} = \dfrac{1}{3}ML^2\text{,}\) given to us, we get

\begin{equation*} I_{\text{cm}} = \left( \dfrac{1}{3} - \dfrac{1}{4} \right)\, ML^2 = \dfrac{1}{12}\,ML^2. \end{equation*}

Subsection 9.7.5 Radius of Gyration

We ask the following question: suppose we replace a rotating body of mass \(M\) by a point particle of the same mass \(M\text{,}\) at what distance should we place this fictitious particle so that its moment of inertia will be the same as that of the original body? This distance is called the radius of gyration, which is denoted by \(R_G\text{.}\)

For instance, the moment of inertia of a disk of mass \(M\) and radius \(R\) about an axis through the center and perpendicular to the disk is

\begin{equation*} I_{\text{disk}}^{\perp} = \dfrac{1}{2} MR^2. \end{equation*}

Replacing the disk by a point mass \(R_G\) away from the axis will mean

\begin{equation*} I_\text{particle} = M R_G^2 = \dfrac{1}{2} MR^2 = I_{\text{disk}}^{\perp}, \end{equation*}

which gives

\begin{equation*} R_G = \dfrac{1}{\sqrt{2}}\,R. \end{equation*}

This is not the only \(R_G\) in a disk. If we rotate the disk about an axis through the center but the axis is in the plane of the face of the disk, then, we will have

\begin{equation*} M R_G^2 = \dfrac{1}{4} MR^2, \end{equation*}

giving

\begin{equation*} R_G = \dfrac{1}{2}\,R. \end{equation*}

Thus, there is not one \(R_G \) per object, but one \(R_G\) per axis, unless the object is fully symmetric, such as a sphere. In that case there is only one \(R_G\text{,}\) which is

\begin{equation*} R_G^{\text{sphere}} = \dfrac{\sqrt{2}}{\sqrt{5}}\, R, \end{equation*}

since moment of inertia of a sphere through any axis through its center is

\begin{equation*} I_{\text{sphere}} = \dfrac{2}{5}\,MR^2. \end{equation*}

Subsection 9.7.6 (Calculus) Moment of Inertia of a Uniform Rod

The non-Calculus derivation of the moment of inertia of a rod about its end done above is difficult to generalize to more complicated objects, such as disk. Here, we introduce the Calculus aproach to the same problem.

We start with noting that moment of inertia will be the sum of moment onertia of all the particles of the rod. Let us look at the infinitesimal mass \(\delta m\) that is between \(r \) and \(r + dr \) from the end of the rod.

Assuming mass is distributed uniformly over the length of the rod, we can immediately write the value of \(\delta m\text{.}\)

\begin{equation*} \delta m = \dfrac{M}{L}\, dr. \end{equation*}

Since this is at a distance \(r \) from the axis, its moment of inertia is

\begin{equation*} \delta I = r^2 \delta m = \dfrac{M}{L}\, r^2 dr. \end{equation*}

Adding the contributions of all the particles can be achieved by integrating this from \(r = 0 \) to \(r = L\text{,}\) giving the following for the moment of inertia of the rod.

\begin{equation*} I = \int_0^L\, \dfrac{M}{L}\, r^2 dr = \dfrac{M}{L}\times \dfrac{L^3}{3}. \end{equation*}

Simplifying this gives us the same answer we found above.

\begin{equation*} I_{\text{rod}}^{\text{axis-at-end}} = \dfrac{1}{3}\, M L^2. \end{equation*}

Subsection 9.7.7 (Calculus) Proof of the Parallel Axis Theorem

Let us choose the \(z \) axis to be the orientation of the two parallel axes, one through the CM and the other through the axis A as shown in Figure 9.72. Let origin be at the CM, which would mean

\begin{equation*} \int x dm = 0,\ \ \int y dm = 0, \ \ \int z dm = 0. \end{equation*}

The moment of inertia about axis through the CM will be

\begin{equation*} I_{\text{cm}} = \int \left( x^2 + y^2 \right)\, dm. \end{equation*}

Figure 9.72. The diagram for parallel axis theorem proof. For clarity, the \(y\) axis has been supressed and we have drawn \(x\) axis in the direction from P to the CM.

If axis A intersects the plane (perpendicular to the axes that contains the CM) at point P with cooridinates \((x_P, y_P, 0) \) with respect to the coordinate system with origin at the CM, then

\begin{equation*} x_P^2 + y_P^2 = d^2. \end{equation*}

With another coordinate system, say P\(x'y'z'\) with origin at P, we get the moment of inertial expression for \(I_{\text{A}} \text{.}\)

\begin{equation*} I_{\text{A}} = \int \left( x'^2 + y'^2 \right)\, dm', \end{equation*}

with

\begin{equation*} x' = x-x_P,\ y' = y-y_P,\ z' = z,\ dm'=dm. \end{equation*}

Substituting this in \(I_{\text{A}}\) we get

\begin{align*} I_{\text{A}} \amp = \int \left( (x-x_P)^2 + (y-y_P)^2 \right)\, dm,\\ \amp = \int \left( x^2 + y^2 \right)\, dm - 2x_P\int xdm - 2y_P\int ydm + d^2\int dm,\\ \amp = I_{\text{cm}} + 0 + 0 + Md^2. \end{align*}

Therefore,

\begin{equation*} I_{\text{A}} = I_{\text{cm}} + Md^2. \end{equation*}

Subsection 9.7.8 (Calculus) Moment of Inertia of a Uniform Body

The method illustrated above for the moment of inertia of a rod, can be generalized for any uniform body. Let \(\delta m\) be an infinitesimal mass element whose distance from the axis is \(r \text{,}\) then its contribution to moment of inertia will be

\begin{equation*} \delta I = r^2 \delta m. \end{equation*}

We are using the notation \(\delta m\) for an infinitesimal mass rather than \(dm\) since we usually do not do an integral over this variable, but rather use it to think about the problem, and replace \(\delta m\) by one of the infinitesimal expressions given below, and then perform appropriate integral.

\begin{equation} I = \int\, r^2 \delta m.\tag{9.36} \end{equation}

The mass \(\delta m\) will be the mass in an infinitesimal line (e.g., a bar) or an area (e.g., a thin disk) or a volume (e.g., a sphere). Depending on the situation, we will get different expressions for \(\delta m\text{.}\)

\begin{equation*} \delta m = \begin{cases} (M/L)\, dr, \amp \text{for mass in a line segment}\\ (M/A)\, dxdy, \amp \text{for mass in a rectagular plane area element}\\ (M/A)\, rdrd\theta, \amp \text{for mass with area in polar coordinates}\\ (M/V)\, dx dy dz, \amp \text{for mass in a rectangular box volume element}\\ (M/V)\, r^2\sin\,\theta\,dr d\theta d\phi, \amp \text{for mass in a spherical element} \end{cases} \end{equation*}

Subsection 9.7.9 (Calculus) Principal Axes and Moment of Inertia Tensor

If a body has a rotational symmetry, we can direct the Cartesian axes to take advantage of that symmetry and simplify the expressions of moment of inertia.

What happens if rotating body does not have a rotational symmetry? Turns out that every rigid body, regardless of shape, has three mutually perpendicular special directions in space, called principal axes. The moment of inertia about these principal axes are called principal moments.

Suppose we choose Cartesian axes along the principal axes, and call the moments of inertia about them to be \(I_{xx}\text{,}\) \(I_{yy}\text{,}\) and \(I_{zz}\text{.}\) Then, the angular momentum vector for any arbitrary rotation with \(\omega = (\omega_x,\ \omega_y,\ \omega_z) \) will have the following components.

\begin{align} \amp L_x = I_{xx}\omega_x, \tag{9.37}\\ \amp L_y = I_{yy}\omega_y, \tag{9.38}\\ \amp L_z = I_{xx}\omega_z. \tag{9.39} \end{align}

In a general situation, if you are not using principal axes for your Cartesian coordinates, then, you would find that a component of the angular momentum, say \(L_x \) depends on all three components of \(\vec \omega\text{.}\)

\begin{equation} L_x = I_{xx}\omega_x + I_{xy}\omega_y + I_{xz}\omega_z,\tag{9.40} \end{equation}

where coefficients \(I_{xy}\) and \(I_{xz} \) of \(\omega_y \) and \(\omega_z\text{,}\) respectivley, are also moments of inertia, called the off-diagonal elements of the moment of inertia tensor. Their formulas are different than the diagonal elements. Similarly, for \(L_y\) and \(L_z\text{.}\) For a curious student, the formulas for various moments of inertia are listed here.

\begin{align} \amp I_{xx} = \int\, (y^2 + z^2)\, dm, \tag{9.41}\\ \amp I_{yy} = \int\, (z^2 + x^2)\, dm, \tag{9.42}\\ \amp I_{zz} = \int\, (x^2 + y^2)\, dm, \tag{9.43}\\ \amp I_{xy} = I_{yx} = -\int\, x\,y\, dm , \tag{9.44}\\ \amp I_{yz} = I_{zy} = -\int\, y\,z\, dm , \tag{9.45}\\ \amp I_{zx} = I_{xz} = -\int\, z\,x\, dm . \tag{9.46} \end{align}

Exercises 9.7.10 Exercises

1. Moment of Inertia of a Disk with a Hole in the Center - Negative Mass Trick.

You cut out a circular hole of radius \(b\) from a disk of radius \(a\) and mass \(M\text{.}\) What is the moment of inertia of the resulting disk with the hole about an axis perpendicular to the disk and passing through the center? Assuming uniform density.

Hint.

Think of hole as another disk with negative mass density.

Answer.

\(\dfrac{1}{2} M a^2 \left( 1 - \dfrac{b^4}{a^4} \right).\)

Solution.

Let \(\rho\) be the density and \(h\) the thickness.

\begin{equation*} \rho = \dfrac{M}{\pi a^2 h}. \end{equation*}

Now, we think of the disk with the hole as a complete disk of radius \(a\) and density \(\rho\) and a second disk of radius \(b\) but of density \(-\rho\text{.}\) This way of treating hole in a material is called the negative mass trick. The moments of inertia of these two disks will be

\begin{align*} I_a \amp = \dfrac{1}{2} M_a a^2 = \dfrac{1}{2} M a^2,\\ I_b \amp = \dfrac{1}{2} M_b b^2 = -\dfrac{1}{2} \pi b^2 h \rho b^2. \end{align*}

We can write \(I_b\) in terms of \(M\) as follows

\begin{equation*} I_b = -\dfrac{1}{2} M \dfrac{b^4}{a^2}. \end{equation*}

Adding the two moments we get

\begin{equation*} I = I_a + I_b = \dfrac{1}{2} M a^2 \left( 1 - \dfrac{b^4}{a^4} \right). \end{equation*}

2. Moment of Inertia of a Disk with Off-Axis Hole - Negative Mass Trick.

You cut out a circular hole of radius \(b\) from a disk of radius \(a\) and mass \(M\text{.}\) The center of the hole is at a distance \(c\) from the axis of rotation, which is perpendicular to the disk and passes through the center. What is the moment of inertia of the resulting disk about the axis through the center? Assuming uniform density.

Hint.

Think of hole as another disk with negative mass density and use parallel axis theorem.

Answer.

\(\dfrac{1}{2} M a^2 \left( 1 - \dfrac{b^2(b^2 + 2c^2)}{a^4} \right).\)

Solution.

First we fill the hole with negative density material to get a complete disk. Thus, replacing the disk with a hole by two complete disks, one of mass \(M\) and radius \(a\) and another of mass \(-M b^2/a^2\) and radius \(b\text{,}\) but rotating with axis to center distance \(c\text{.}\)

The moment of inertia of the off-axis disk can be obtained by applying the parallel axis theorem. Thus, the moments of inertia of the two disks are

\begin{align*} I_a \amp = \dfrac{1}{2} M a^2 \\ I_b \amp = -\dfrac{1}{2} M \dfrac{b^2}{a^2} b^2 - M \dfrac{b^2}{a^2} c^2 \end{align*}

Therefore, the moment of inertial of the disk with the hole is

\begin{equation*} I = I_a + I_b = \dfrac{1}{2} M a^2 \left( 1 - \dfrac{b^2(b^2 + 2c^2)}{a^4} \right). \end{equation*}

3. (Calculus) Moment of Inertia of Rod about Axis Through the Center.

Derive the expression for the moment of inertia of a uniform rod of mass \(M\) and length \(L\) about an axis through its center and perpendicular to the rod.

Hint.

Set up moment of inertial of an element at \(x\) away from axis.

Answer.

\(\dfrac{1}{12}ML^2\)

Solution.

Figure 9.75 shows the setup for the calculaton. We place the rod symmetrically on the \(x\)axis. Looking at the moment of inertia of a segment at distance \(x\) from the axis we note that the moment of inertial of \(\delta m\) in the segment will be

\begin{equation*} \delta I = \delta m\, x^2 = (M/L)dx\, x^2. \end{equation*}

Figure 9.75. Figure for Exercise 9.7.10.3 solution.

Integrating this from \(x=-L/2\) to \(x=L/2\) will give the answer we seek.

\begin{align*} I \amp = (M/L)\int_{-L/2}^{L/2}\, x^2 dx = 2(M/L)\int_{0}^{L/2}\, x^2 dx, \\ \amp = \dfrac{2M}{L}\, \dfrac{1}{3}\,\left( \dfrac{L}{2}\right)^3 = \dfrac{1}{12}\,ML^2. \end{align*}

4. (Calculus) Moment of Inertia of Triangular Plate about an Axis Through the Corner.

Derive the expression for the moment of inertia of a uniform right-angled triangle of mass \(M\text{,}\) base \(b\text{,}\) and height \(h\) about an axis through the corner of base and hypoteneus and parallel to the height side.

Hint.

Place axes with origin at the corner through which axis passes and \(x\) axis along the base. Set up moment of inertia of an element at \(x\) away from axis.

Answer.

\(\dfrac{1}{2} M b^2\text{.}\)

Solution.

Figure 9.76 shows the setup for the calculaton. We place origin at the corner through which axis passes and point \(x\) axis along the base. The axis of rotation is the \(y\) axis.

Now, we look at element of width \(dx\) and height \(y\) at a distance \(x\) from the axis. Its moment of inertia is

\begin{equation*} \delta I = \delta m\, x^2 = \left( \dfrac{M}{A}\, ydx \right)\, x^2, \end{equation*}

where \(A = (1/2)bh\text{,}\) the area of the triangle. Here \(y = (h/b) x\text{.}\) Therefore, we have for the moment of inertia of the element as

\begin{equation*} \delta I = \dfrac{Mh}{Ab} \, x^3 dx. \end{equation*}

Integrating from \(x=0\) to \(x=b\) will give us the answer.

\begin{align*} I \amp = \dfrac{Mh}{Ab} \, \int_0^b\, x^3 dx = \dfrac{Mh}{Ab}\times \dfrac{b^4}{4}. \end{align*}

We can simplify it

\begin{equation*} \dfrac{2Mh}{bhb}\times \dfrac{b^4}{4} = \dfrac{1}{2} M b^2. \end{equation*}

5. (Calculus) Moment of Inertia of Right Triangular Plate About one Edge.

Derive the expression for the moment of inertia of a uniform right-angled triangle of mass \(M\text{,}\) base \(b\text{,}\) and height \(h\) about an axis coincident with the height side.

Hint.

Choose \(y\) axis to be axis of rotation. Set up moment of inertia of an element at \(x\) away from axis.

Answer.

\(\dfrac{1}{6}Mb^2\)

Solution.

Figure 9.76 shows the setup for the calculaton. We place origin at the corner of right-angle. With axis of rotation to be the \(y\) axis, we have base along \(x\) axis.

Now, we look at element of width \(dx\) and height \(y\) at a distance \(x\) from the axis. Its moment of inertia is

\begin{equation*} \delta I = \delta m\, x^2 = \left( \dfrac{M}{A}\, ydx \right)\, x^2, \end{equation*}

where \(A = (1/2)bh\text{,}\) the area of the triangle. Here \(y = h - (h/b) x\text{.}\) Therefore, we have for the moment of inertia of the element as

\begin{equation*} \delta I = \dfrac{M}{A} \, \left( h x^2 -(h/b) x^3 \right) dx. \end{equation*}

Integrating from \(x=0\) to \(x=b\) will give us the answer.

\begin{align*} I \amp = \dfrac{M}{A} \times \dfrac{hb^3}{12} = \dfrac{1}{6}Mb^2. \end{align*}

6. (Calculus) Moment of Inertia of Thin Disk about an Axis Through the Center and Perpendicular to Disk.

Derive the expression for the moment of inertia of a uniform thin disk of mass \(M\) and radius \(R\) about an axis through the center and perpendicular to the disk.

Hint.

Think of a disk being made up of rings. A ring has all masses same distance from the center. Therefore, moment of inertia of ring will be \(m r^2\text{.}\) You need to think of how to add them.

Answer.

\(\dfrac{1}{2}\,MR^2\text{.}\)

Solution.

Figure 9.78 shows setup for claculations. The axis in coming-out-of page in the figure.

Figure 9.78. Figure for Exercise 9.7.10.6 solutiuon.

Now we look at an element of the disk in the shape of a ring between \(r\) and \(r+dr\text{.}\) All masses in the ring would rotated from the axis at a distance \(r\text{.}\) Therefore, moment of inertia of the ring element will be

\begin{equation*} \delta I = \delta m \times r^2 = \left( \dfrac{M}{A}\, 2\pi r dr \right)\, r^2, \end{equation*}

where \(A=\pi R^2\) and \(2\pi r dr \) is the area of the ring. We would integrate this from \(r=0\) to \(r=R\) to find \(I\text{.}\)

\begin{align*} I \amp = \dfrac{2M}{R^2}\, \int_0^R r^3 dr = \dfrac{1}{2}\,MR^2. \end{align*}

7. (Calculus) Moment of Inertia of Thin Disk about an Axis Through the Center and Coplanar to Disk.

Derive the expression for the moment of inertia of a uniform thin disk of mass \(M\) and radius \(R\) about an axis through the center and coplanar to the disk, i,e., along one of its diameter.

Hint.

Take \(y\) axis to be axis of rotation and an element between \(x\) anx \(x+dx\) parallel to \(y\) axis.

Answer.

\(\dfrac{1}{4}\,MR^2\text{.}\)

Solution.

Figure 9.79 shows setup for claculations. The axis is along \(y\) axis.

Figure 9.79. Figure for Exercise 9.7.10.7 solutiuon.

Now we look at an element of the disk in rectangular shape between \(x\) and \(x+dx\text{.}\) The area of the element will be \(2ydx\) since the length is \(2y\) and width \(dx\text{.}\) The \(y\) in the element area is

\begin{equation*} y = \sqrt{R^2 - x^2}. \end{equation*}

All masses in the element would rotated from the axis at a distance \(x\text{.}\) Therefore, moment of inertia of the ring element will be

\begin{align*} \delta I \amp = \delta m \times x^2 = \left( \dfrac{M}{A}\, 2ydx \right)\, x^2,\\ \amp = \dfrac{2M}{\pi R^2}\, x^2 \sqrt{R^2 - x^2}\, dx \end{align*}

We would integrate this from \(x=-R\) to \(r=R\) to find \(I\text{.}\) Since integrand is an even function of \(x\text{.}\) That would mean we will get \(2\) times integral from \(x=0\) to \(r=R\text{.}\)

\begin{align*} I \amp = \dfrac{2M}{\pi R^2}\,2\times\,\int_0^R x^2 \sqrt{R^2 - x^2}\, dx. \end{align*}

The integral is difficult to do. I typed the command integrate x^2*sqrt(R^2-x^2), x in https://www.wolframalpha.com/

www.wolframalpha.com/

and found the following answer.

\begin{align*} \int_0^R x^2 \sqrt{R^2 - x^2}\, dx \amp = \dfrac{1}{8}\left[ x\sqrt{R^2 - x^2}\left( 2x^2 - R^2\right) \right.\\ \amp \ \ + R^4\tan^{-1}\left.\left( \dfrac{x}{R^2-x^2}\right)\right]_0^R,\\ \amp = \dfrac{1}{8}\left[ 0 - 0 + \dfrac{\pi}{2} - 0\right] = \dfrac{\pi}{16}. \end{align*}

Therefore,

\begin{equation*} I = \dfrac{4M}{\pi R^2} \times \dfrac{\pi}{16} = \dfrac{1}{4}\,MR^2. \end{equation*}

8. (Calculus) Moment of Inertia of a Sphere about an Axis Through the Center.

Derive the expression for the moment of inertia of a uniform sphere of mass \(M\) and radius \(R\) about an axis through the center of the sphere.

Hint.

With \(z\) axis as axis of rotation, consider thin disk between \(z\) and \(z+dz\text{.}\)

Answer.

\(\frac{2}{5}MR^2\text{.}\)

Solution.

Figure 9.80 shows setup for claculations. The axis of rotation is \(z\) axis in the figure.

Figure 9.80. Figure for Exercise 9.7.10.8 solutiuon.

Now we look at an element of the sphere in the shape of a disk perpendicular to \(z\) axis between \(z\) and \(z+dz\text{.}\) The radius of the disk \(r\) is

\begin{equation*} r = \sqrt{R^2 - z^2}. \end{equation*}

Therefore, volume of the element is

\begin{equation*} dV = \pi r^2 dz =\pi\, \left(R^2 - z^2 \right)\, dz. \end{equation*}

The mass of the disk is

\begin{equation*} dm = \dfrac{M}{V}\, dV = \dfrac{M}{V}\, \pi\, \left(R^2 - z^2 \right)\, dz, \end{equation*}

where \(V = \frac{4}{3}\pi R^3\text{.}\) The moment of inertia of this element about \(z\) axis is

\begin{equation*} dI = \dfrac{1}{2}\, dm\, r^2. \end{equation*}

This gives

\begin{equation*} dI = \dfrac{M}{2V}\, \pi\, \left(R^2 - z^2 \right)^2\, dz. \end{equation*}

Integrating this from \(z=-R\) to \(z=R\text{,}\) which is same as \(2\times\) inegration from \(z=0\) to \(z=R\) due to evenness of the integrand, gives the answer.

\begin{equation*} I = \dfrac{\pi M}{V}\, R^5\,\left( 1 - \frac{2}{3} + \frac{1}{5}\right) = \dfrac{2}{5}MR^2. \end{equation*}

Prev Top Next