Light as Electromagnetic Waves

Section 53.2 Light as Electromagnetic Waves

Young's double-slit experiment demonstrates that light is a wave since light forms interference expected from waves. That light is a wave consisting of intertwined electric and magnetic waves was shown mathematically by James Clerk Maxwell. To arrive at this conclusion Maxwell considered a region of space that has no currents or charges, so-called empty space or vacuum and sought the solution of his equations. This gives the following set of equations for \(\vec E\) and \(\vec B\text{.}\)

\begin{align} \amp \vec{\nabla}\cdot \vec E = 0\label{eq-max-empty-1-1}\tag{53.2.1}\\ \amp \vec{\nabla}\cdot \vec B = 0\label{eq-max-empty-2-1}\tag{53.2.2}\\ \amp \vec{\nabla}\times \vec E = -\frac{\partial \vec B}{\partial t}\label{eq-max-empty-3-1}\tag{53.2.3}\\ \amp \vec{\nabla}\times \vec B =\mu_0\epsilon_0 \frac{\partial \vec E}{\partial t}\label{eq-max-empty-4-1}\tag{53.2.4} \end{align}

Is there a way to know the characteristics of the electric and magnetic fields that satisfy these equations? It turns out that taking the curl of Eq. (53.2.3) and using Eq. (53.2.1) and (53.2.4) shows that the electric field obeys the wave equation.

\begin{equation} \nabla^2\vec E = \frac{1}{\epsilon_0\mu_0}\: \frac{\partial^2\vec E}{\partial t^2}.\label{eq-max-empty-e-field-wave}\tag{53.2.5} \end{equation}

Similarly the curl of (53.2.4) gives the result that magnetic field also obeys the same wave equation.

\begin{equation} \nabla^2\vec B = \frac{1}{\epsilon_0\mu_0}\: \frac{\partial^2\vec B}{\partial t^2}.\label{eq-max-empty-b-field-wave}\tag{53.2.6} \end{equation}

These equations have solutions of the form \(\vec F = \vec F_0 \cos( \vec k \cdot r - \omega t + \delta)\text{,}\) which shows that vacuum has electric and magnetic field waves with speed

\begin{equation*} v = \frac{\omega}{|\vec k|} = \frac{1}{\sqrt{\epsilon_0\mu_0}}. \end{equation*}

When you plug in the experimental values of \(\epsilon_0 = 8.85\times 10^{-12}\:\textrm{C}^2/\textrm{N.m}^2\) and \(\mu = 4\pi\times10^{-7}\:\textrm{T.m/A}\) you find the value of speed to be \(3\times 10^{8}\text{ m/s}\text{,}\) same as the speed of light \(c\text{.}\)

\begin{equation} v = 3 \times 10^8 \text{ m/s}.\tag{53.2.7} \end{equation}

Maxwell found this speed to be too close to the speed of light to be a simply a coincidence. He then claimed that light itself was these waves and proposed that speed of light \(c\) in vacuum was related to electric susceptibility and magnetic permeability of vacuum.

\begin{equation} c = \frac{1}{\sqrt{\epsilon_0\mu_0}}.\tag{53.2.8} \end{equation}

Subsection 53.2.1 Hertz's Experiment

After Maxwell predicted the existence of the electromagnetic waves in 1873, many scientists tried to produce them in the laboratory. The first person to succeed was the German physicist Heinrich Hertz who produced and detected radio waves in 1888. Hertz's equipment consisted of a radiator and a detector/receiver, a replica of which is shown in Figure 53.2.1.

Figure 53.2.1. A replica of Heinrich Hertz'e apparatus for production and detection of radio waves. Photo courtesy of http://www.sparkmuseum.com/HERTZ.HTM.

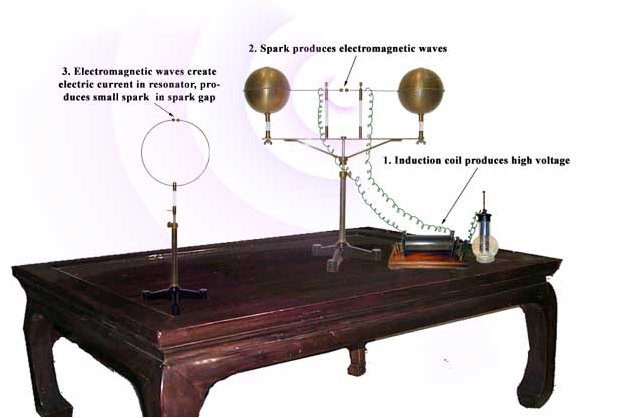
The radiator was a pair of one-meter rods with a spark gap in the center and two large spheres at the other ends of the wires to adjust the capacitance for resonance condition. The rods were connected to an induction coil that supplied a high voltage. The receiver was simply a loop of wire with a small gap. When the rods of the radiator setup were given strong enough voltage, a spark was generated across the gap and the current would oscillate back and forth across the gap and along the rods.

The receiver consisted of a loop of wire with a tiny gap. When an electromagnetic waves passes through the area of the loop, the magnetic field in the electromagnet wave would cause the magnetic flux to change which would result in an induced EMF in the wire. The induced EMF caused a spark across the tiny gap in the ring.

Hertz conducted many experiments measuring the wavelength and speed of these waves and showed that they travel at the predicted speed of light. He also showed that the radio waves refracted and reflected similar to light thus lending a strong support to Maxwell's assertion that the light was an electromagnetic wave. When his students asked what use can be made of this discovery, he apparently replied, ``It's of no use whatsoever. This is just an experiment that proves Maestro Maxwell was right - we just have these mysterious electromagnetic waves that we cannot see with the naked eye. But they are there.'' But, here we are today about 100 years later with our cell phones and WiFi none of which would be possible without Hertz's discoveries. To honor Hertz the unit of frequency Hertz (Hz) is named after Heinrich Hertz. One Hertz equals one cycle per second.

Subsection 53.2.2 Electromagnetic Spectrum

A wide range of electromagnetic waves have been either found in nature or produced in the laboratory. The collection of all EM waves is called the electromagnetic spectrum. They are usually categorized in various sub-ranges or bands as shown in Figure 53.2.2. Note the all important visible light occupies a minuscule band compared to the available EM spectrum.

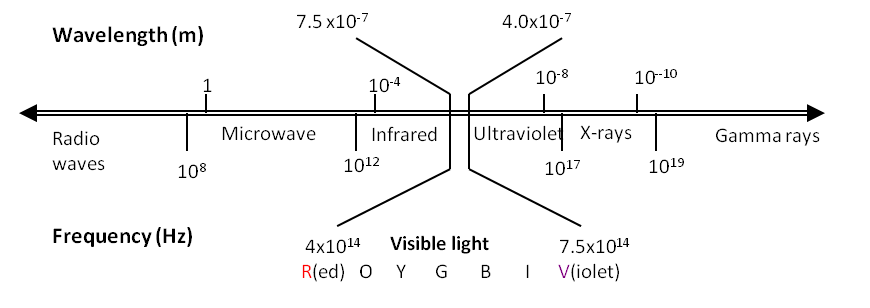
Figure 53.2.2. The electromagnetic spectrum. The names of the bands and corresponding frequencies are given below the double line. Above the band some representative wavelengths in vacuum are given. Note that the boundaries between different bands are arbitrary.

The frequency of an electromagnetic wave is same as the frequency of vibrating charges that produce it. Hertz's waves had a frequency of about \(10^6\) cycles per second. These waves are now called radio waves. The visible light is also an electromagnetic wave but with considerably higher frequency than the radio waves. Visible light have frequency approximately between \(4 \times 10^{14}\text{ Hz}\) (red) and \(7.5 \times 10^{14} \text{ Hz}\) (violet) compared to the radio waves that have frequency less than \(10^8\) Hz.

The electromagnetic waves of frequency as high as \(10^{10}\text{ Hz}\) are usually produced in the laboratory using a similar setup used by Hertz. It consists of an antenna upon which an oscillating voltage is applied which radiates electromagnetic waves. The EM waves of higher frequencies are not produced in the laboratory by this method. You can see from the fundamental wave relation that a higher frequency would correspond to a lower wavelength. To produce a visible light of frequency \(4 \times 10^{14} \text{ Hz}\text{,}\) you would need an antenna less than one micrometer in length and a circuitry that can oscillate at \(4 \times 10^{14}\text{ Hz}\text{,}\) both of which are not currently available.