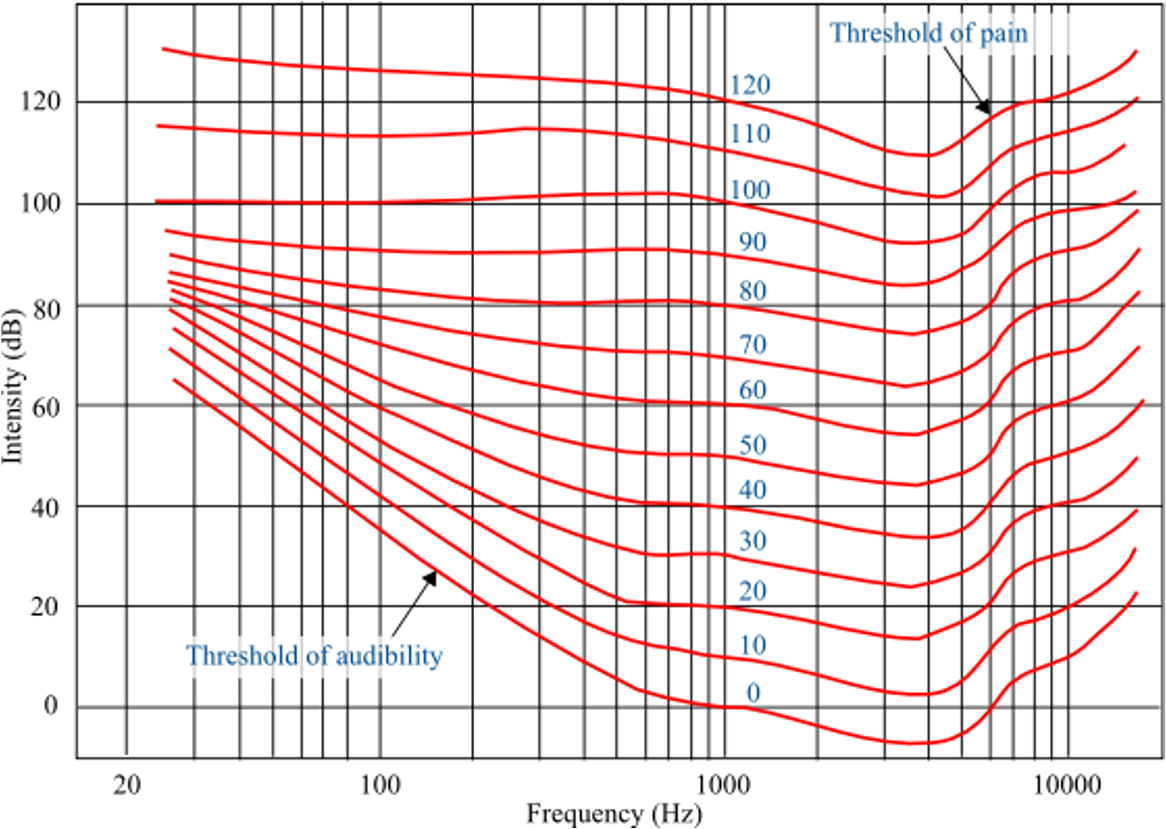
The intensity of sound that a human can hear has a very wide range, from approximately \(10^{-12}\text{ W/m}^2\) to \(1\text{ W/m}^2\text{.}\) In properties that have such wide range of interest, it is often the practice to introduce logarithmic scale. In the case of sound, the logarithm scale called decibel which uses base-10 log. Since the argument of log has to be dimensionless, we define the unit of \(\text{bel}\) by the log of a ratio of intensity \(I\) to a reference intensity \(I_0\text{.}\)
\begin{equation*}
\text{Intensity in bel} = \log_{10}\, \frac{I}{I_0}.
\end{equation*}
A more common unit is decibel. You may recall that a deci-something is \(\frac{1}{10}\) of that thing. When we express the intensity in decibels, we call it the level of sound relative to the reference. We denote the level by the Greek letter \(\beta\) (beta) and the unit by \(dB\text{.}\)
\begin{equation}
\beta (\text{in dB}) = 10\ \log_{10}\, \frac{I}{I_0}.\tag{15.10}
\end{equation}
Of course, given dB level \(\beta\text{,}\) we can get intensity by inverting this.
\begin{equation}
I = I_0\times 10^{\beta/10}.\tag{15.11}
\end{equation}
Most commonly, the reference intensity is taken to be the lowest threshold of The reference intensity for sound wave is \(10^{-12}\text{ W/m}^2\text{,}\) approximately the threshold of normal human hearing at \(1000\text{ Hz}\) of frequency.
\begin{equation*}
I_0 = 10^{-12}\text{ W/m}^2.
\end{equation*}
Thus, if the intensity of some sound is \(1000\)-times the reference, then it will have a decibel of 30. Here is how:
\begin{equation*}
\beta (\text{in dB}) = 10\ \log_{10}\, 10^3 = 10\times 3 = 30.
\end{equation*}
Log base 10 picks out the power of 10. Therefore, log base 10 of \(1000\) is just \(3\text{.}\) The range of intensity for human hearing amounts to a range of \(0\) to \(120\text{ dB}\text{.}\) A useful information to remember is that a \(3\text{-dB}\) drop in intensity corresonds to intensity becoming half as much since we have
\begin{equation*}
10\ \log_{10}\, \frac{1}{2} \approx - 3.
\end{equation*}
Since intensity of a wave is proportional to the square of the amplitude of the wave, we can express sound level in terms of amplitude as well. Let \(A\) and \(A_0\) be the amplitudes of the test wave and the reference wave respectively, i.e.,
\begin{equation*}
I = a A^2,\ \ \ \text{and}\ \ \ I_0 = a A_0^2,
\end{equation*}
where \(a\) is some common factor which will cancel out in the ratio. this gives sound level \(\beta\) in \(\text{dB}\) to be
\begin{equation*}
\beta (\text{in dB}) = 20\ \log_{10}\, \frac{A}{A_0}.
\end{equation*}
Beware of the change in multicaptive factor to the log. This 20 and 10 is a source of common confusion.