Example 6.27. Net Force on a Box Pulled by Two Forces in Perpendicular Directions.
A box is pulled by a force of \(40\text{ N}\) in the horizontal direction and a force of \(30\text{ N}\) also horizontally but at an angle of \(90^{\circ}\) to the direction of the other force. Find the magnitude and direction of the net force by these two forces in the horizontal plane.

Answer.
\(50\ N,\ 37^{\circ}\) counterclockwise from the postitive \(x \) axis.
Solution.
This problem can be done either graphically or analytically by setting up a coordinate system and using the components. We will do it analytically here. First, note that the forces of weight and normal force from the floor are not in the horizontal plane, therefore, we will ignore them since the question is only about forces that act in the horizontal plane.
First, we draw the forces in a figure so that the tails of the force vectors of interest are at the same point. This diagram of forces is called a free-body diagram. Then, we pick axes for a Cartesian coordinate system that would be very helpful in calculating the components as illustrated in the figure shown here.
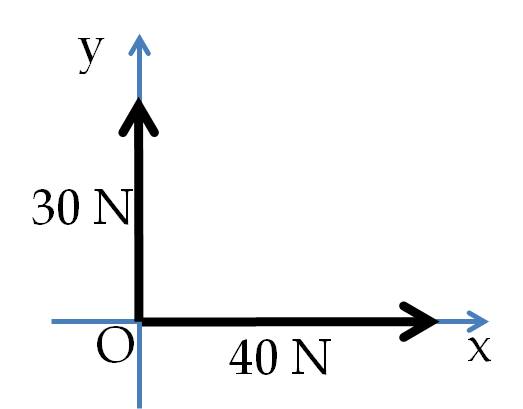
Computational Steps. Using the chosen axes, we compute the Cartesian components of each force. Note that while the magnitude of a force is always positive, the components can be positive or negative. Finally, we add the \(x \) components of the forces separately from their \(y \) components to obtain the \(x \) and \(y \) components of the net force. The strength of the force is the magnitude. Therefore, we calculate the magnitude and direction of the net force from the \(x \) and \(y \) components as we would for any vector quantity.
The implementation in the present case. The table below summarizes the components found for each force.
| Force | \(x\)-component | \(y\)-component |
| \(\vec F_1 \) | \(40\text{ N} \) | \(0\) |
| \(\vec F_2 \) | \(0\) | \(30\text{ N} \) |
For simplicity in writing, let us denote the net force by \(\vec F \) rather than \(\vec F_{\text{net}}\text{.}\) Therefore, the \(x \) and \(y \) components of the net force are
\begin{align*}
\amp F_x = 40 + 0 = 40\text{ N}\\
\amp F_y = 0 + 30 = 30\text{ N}
\end{align*}
Therefore, the magnitude of the force is
\begin{equation*}
F = \sqrt{F_x^2+F_y^2}=\sqrt{40^2+30^2} = 50\ N,
\end{equation*}
and the angle from the positive \(x \) axis is
\begin{equation*}
\theta =\arctan\left(\frac{F_y}{F_x}\right)=\arctan\left(\frac{30}{40}\right) = 37^{\circ}.
\end{equation*}
Since \((40,\ 30)\) is in the first quadrant, the direction is \(37^{\circ}\) counterclockwise from the postitive \(x \) axis.







