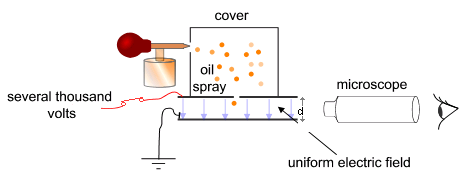
When Robert Millikan studied one of the oil drops he measured the falling time \((t_0)\) with no electric field and rising time \((t_E)\) with electric field on for a distance of 10.21 mm. The successive measurements for the falling and rising times showed a consistent value for the fall time without the electric field but a wide variation of the time with the electric field on.
\begin{align*}
(t_0, t_E) = \amp [(18.689, 17.756), (18.73, 17.778), (18.686, 45.978), (18.726, 45.87),\\
\amp (18.772, 45.716), (18.74, 45.758), (18.724, 694.0), (18.72, 27.95), \\
\amp (18.816, 118.388), (18.816, 45.03), (18.716, 34.564), (18.804, 44.826),\\
\amp (18.746, 117.198), (18.746, 44.784)]
\end{align*}
The variation in the times when the electric field was on was attributed to different charges on the same droplet. By assuming that the difference in the charges of the same droplet must be an integral multiple of a fundamental unit of charge he was able to deduce a value of the electronic charge. To apply the electric field a voltage of \(5100\text{ V}\) across the plates separated by 16 mm was applied. The density of the oil was \(0.9199 \text{ g/cm}^3\) and the viscosity of air was \(1.824 \times 10^{-5}\:\textrm{kg.m/s}\text{.}\) Use this data to deduce the electronic charge.
Hint.
Answer.
\(1.74\times 10^{-19}\:\textrm{C}\text{.}\)
Solution.
We want the multiple readings of \((v+v_E)\) to be in proportion of integers. First, we will average \(t_0\) to get the average time for the fall without electric field. This will give us the best value for \(v\text{.}\)
\begin{equation*}
v = \frac{h}{t_0} = \frac{10.21\:\textrm{mm}}{ 18.745\:\textrm{s}} = 0.545\:\textrm{mm/s}.
\end{equation*}
Various rise times give different values of \(v_E\) corresponding to different amount of charge on the drop. In Eq. \ref{eq:millikan-oil-drop-integer}, they are referred to \(v_1\) and \(v_2\) for two such data.
\begin{align*}
v_E (\textrm{mm/s})= \amp [ 0.575, 0.574, 0.222, 0.223, 0.223, 0.223, \\
\amp 0.0147, 0.365, 0.0862, 0.227, 0.295, 0.228, 0.087, 0.228]
\end{align*}
Suppose you sibtract 1 from both sides of Eq. \ref{eq:millikan-oil-drop-integer}. you will get the following for the difference of two charges.
\begin{equation*}
q_1 - q_2 = \frac{v_1-v_2}{v+v_2}\:q_2.
\end{equation*}
We require that this be an integer multiple of the electronic charge \(e\text{.}\)
\begin{equation*}
\frac{v_1-v_2}{v+v_2}\:q_2 = n e.
\end{equation*}
Therefore,
\begin{equation*}
v_1-v_2 = n e_2,\ \ e_2 = e/[(v+v_2)q_2].
\end{equation*}
So, if we compare all other velocities to a particular velocity we should get integers times some fixed number \(e_2\text{.}\) Therefore, let us look at the difference between the velocities with the smallest velocity, which is 0.0147 mm/s. We get the following
\begin{align*}
v_1 - v_2 (\textrm{mm/s})= \amp [ 0.56, 0.56, 0.21, 0.21, 0.21, 0.21,\\
\amp 0, 0.35, 0.07, 0.21, 0.28, 0.21, 0.07, 0.21]
\end{align*}
Now, we can try to get smallest integers \(n\) for each \(v_1-v_2\text{.}\) Suppose, we divide each by the smallest one in the list here, which would be 0.07 mm/s.
\begin{align*}
(v_1 - v_2 \amp (\textrm{mm/s}))/(0.07 \textrm{mm/s})= [ 7.8, 7.8, 2.9, 2.9, 2.9, 2.9,\\
\amp 0, 4.9, 1.0, 3.0, 3.9, 3.0, 1.0, 3.0]
\end{align*}
Let the charge was \(q_0\) for the reference case and \(q_1\) when the difference in rise time was 0.07 mm/s. The formula for each charge is
\begin{equation*}
q = \frac{d}{V} (v + v_E) 6\pi \eta \sqrt{\frac{9\eta v}{2\rho g}}.
\end{equation*}
We have
\begin{equation*}
d = 16\:\textrm{mm},\ \ V = 5100\:\textrm{V},\ \ \eta = 1.824 \times 10^{-5}\:\textrm{kg.m/s}, \rho = 0.9199\: \textrm{g/cm}^3.
\end{equation*}
Therefore,
\begin{align*}
q_0 \amp = \frac{0.016\:\textrm{m}}{5100\:\textrm{V}} ( 0.000545\:\textrm{m/s}+ 0.0000147\:\textrm{m/s}) 6\pi \times 1.824 \times 10^{-5}\:\textrm{kg.m/s} \\
\amp \ \ \ \sqrt{\frac{9\times 1.824 \times 10^{-5}\:\textrm{kg.m/s}\times 0.000545\:\textrm{m/s}}{2\times 919.9\:\textrm{kg/m}^3\times 9.81\:\textrm{m/s}^2}} = 1.344 \times 10^-18\:\textrm{C}.
\end{align*}
\begin{align*}
q_1 \amp = \frac{0.016\:\textrm{m}}{5100\:\textrm{V}} ( 0.000545\:\textrm{m/s}+ 0.000087\:\textrm{m/s}) 6\pi \times 1.824 \times 10^{-5}\:\textrm{kg.m/s} \\
\amp \ \ \ \sqrt{\frac{9\times 1.824 \times 10^{-5}\:\textrm{kg.m/s}\times 0.000545\:\textrm{m/s}}{2\times 919.9\:\textrm{kg/m}^3\times 9.81\:\textrm{m/s}^2}} = 1.518 \times 10^-18\:\textrm{C}.
\end{align*}
The difference in their charges is
\begin{equation*}
q_1 - q_0 = 1.518 \times 10^-18\:\textrm{C} - 1.344 \times 10^-18\:\textrm{C} = 1.74\times 10^{-19}\:\textrm{C}.
\end{equation*}
If we assume that the smallest difference in the rise times occur as a result of capture of one electron by the drop, we can deduce that the electronic charge is \(e =1.74\times 10^{-19}\:\textrm{C}\text{,}\) which is not too far from the accepted value of \(e =1.60\times 10^{-19}\:\textrm{C}\text{.}\) Working with other pair of data produced additional results for \(e\text{.}\)