Section 52.9 Ordering of elements
Subsection 52.9.1 X Rays and the Nuclear Charge
The ionization energy plot in Figure 52.81 below shows how the energetics of the weakest bound electron in the atom. Due to the screening by the core electrons the ionization energy of the outer electrons do not rise steadily with the atomic number \(Z\text{.}\) However, if we were to examine the energetics of the most tightly bound electron in the atom, they will be the in innermost orbital, i.e. the electron in the K shell or \((n=1,l=0)\) orbital, and will not see much of the screening effect.
The British physicist argued that the energies of the electrons in various elements will yield information about the nuclear charge directly. He bombarded samples of metals with electrons in the keV range, which was sufficient to knock out inner K shell electrons. When electrons in other shells fell in the empty K shell they would emit photons in the X-ray range. Depending on which electrons fell to fill the empty K shell the emitted photon would be of different wavelength. Thus, we get \(K_{\alpha}\) line when an electron falls from L shell to the K shell, \(K_{\beta}\) line when an electron falls from M shell to the K shell, \(K_{\gamma}\) line when an electron falls from N shell to the K shell, etc. The collection of the photons resulting from falling of electrons from different shells to the K shell is called the K series. There is a similar L series for transitions associated with electrons from M, N, etc, falling into empty L shell. And similarly M, N, ..series.
H.G.J. Mosely conducted many experiments with many materials and tabulated the wavelengths and frerquencies of emitted lines in the K and L series and interpreted them using the Bohr model. Suppose an electron is knocked out of the K shell of an element of atomic number \(Z\text{.}\) Now, there would be only one electron left in the K shell which will shield \(Z\) by 1 so that the effective \(Z\) seen by electrons in the L shell will be \(Z-1\text{.}\) An electron jumping from the L shell (\(n=2\)) into the K shell (\(n=1\)) will release of a photon, the \(K_{\alpha}\) photon whose energy will be
\begin{align}
E_{K_{\alpha}} \amp = -\frac{1}{4\pi \epsilon_0} \frac{e^2}{2a_0}\:\frac{(Z-1)^2}{2^2} - \left[ -\frac{1}{4\pi \epsilon_0} \frac{e^2}{2a_0}\:\frac{(Z-1)^2}{1^2}\right]\notag\\
\amp = \frac{1}{4\pi \epsilon_0} \frac{e^2}{2a_0}\:\frac{3(Z-1)^2}{4}.\tag{52.77}
\end{align}
Therefore, the wavelength for the emitted photon will be \[ \lambda_{K_{\alpha}} = \frac{hc}{E_{K_{\alpha}} }. \] As an example, let us work out the energy for \(K_{\alpha}\) photon for iron, whose \(Z\) is 26. Plugging in the numerical values we obtain \[ E_{K_{\alpha}} = 6.374\:\textrm{keV},\ \ \lambda_{K_{\alpha}} = 1.95\times 10^{-10}\:\textrm{m}. \] Expressing Eq. (52.77) for the frequency of the photon \(f_{K_{\alpha}}\) we find
\begin{equation}
hf_{K_{\alpha}} = \frac{1}{4\pi \epsilon_0} \frac{e^2}{2a_0}\:\frac{3(Z-1)^2}{4}. \tag{52.78}
\end{equation}
This equation shows that \(Z\) shoudl go as the square-root of the frequency.
\begin{equation}
Z = 1 + C\sqrt{f_{K_{\alpha}} }, \tag{52.79}
\end{equation}
where \[ C = 4\pi \epsilon_0 h \frac{8a_0}{3e^2}. \] Mosely used this equation to show that if the successive elements in the periodic table were placed one unit apart on the ordinate and square root of the frequency of the corresponding \(K_{\alpha}\) line was placed on the abscissa, he got a perfect straight line only if introduced gaps at \(Z =\) 43, 61, and 75 for the straight line to work out properly. This led him to predict the existence of elements of atomic number 43, 61, and 75, which have since been discovered - Technicium (\(Z\) = 43) and Prometium (\(Z\) = 61) were made arificially and Rhenium (\(Z\) = 75) was isolated from natural sources.
Before Mosely’s X-ray spectra of elements, the atomic numbers did not have the interpretation of the number of protons in the nucleus but rather place holders in the periodic table and the elements were ordered according to the atomic weight. As a result, some of the orders were not in the order of increasing \(Z\text{.}\) For instance, in the periodic table before Mosely, Ni was placed ahead of Co since Ni had atomic weight 58.7 and Co had atomic weight 58.9. Moseley showed that Co had \(Z=27\) and Ni had \(Z=28\text{,}\) and so, Co should be placed before Ni.
Subsection 52.9.2 The Madelung Rule and the Aufbau Principle
The Aufbau principle forwarded by Neils Bohr and Wofgang Pauli helps in understanding the order of chemical elements in the periodic table in terms of the electron configurations. According to the Aufbau principle, “The orbitals of lower energy are filled in first with the electrons and only then the orbitals of high energy are filled.” Each orbital corresponds to particular values of \(n, l, m_l\) and can hold up to two electrons, one with an up spin and the other with a down spin. This principle makes sense from the energy perspective but it is difficult to implement if we do not know the energies of various orbitals.
In multi-electron systems the problem of detemining the energies of orbital by solving the Schr\"odinger equation is complicated by the fact that now we also have electron-electron interactions and the energy due to interaction between the orbital angular momentum and spin angular momentum, the so-called L-S coupling. The energy of levels now would depend on \(n\) and other qunatum numbers, not just \(n\text{.}\)
Instead, we turn to empirically derived rules. The most successful of these rules is due to Erwin Madelung, who, in 1936, put forth two principles by which electrons in a multielectrons fill up the “orbitals” of the hydrogen atom problem. The Madelung rule for the electronic configuration of multielectron atoms has two parts:
- The energy increases with increasing \((n + l)\text{.}\)
- For equal \((n + l)\) the energy of higher \(n\) is higher.
The \(n+l\) rule is variously known as the Madelung rule, Klechkowski rule, or the diagonal rule. This rule combined with the Aufbau principle gives the following order for filling up the shells in successively higher energy orbitals.
\begin{align*}
\amp \text{Orbital: } 1s \lt 2s \lt 2p \lt 3s \lt 3p \lt 4s \lt 3d \lt 4p \lt 5s\\
\amp n+l: 1,\ 2,\ 3,\ 3\, 4\, 4\, 5\, 5\, 5\\
\amp n: 1,\ 2,\ 2,\ 3\, 3\, 4\, 3\, 4\, 5
\end{align*}
The order of filling of orbitals based on Madelung rule runs into questions about how to handle spin, especially when filling the orbitals with degenracies, such as the \(p\text{,}\) \(d\text{,}\) \(f\) orbitals. In the case of the \(s\)-orbital, the second electron in the same \(s\)-orbital will have to be of opposite spin to that of the first electron placed in that orbital due to the Pauli’s exclusion principle. But for other orbitals, such as the \(2p\) orbital, the second electron can be in another \(m_l\) subsubshell with the same spin as the first electron without violating the Pauli’s exclusion principle. It turns out that it is preferable to place electron in separate \(m_l\) orbitals rather than the same \(m_l\) orbital since that reduces repulsion between the two electrons and hence gives a lower energy state. This aspect of filling states is called the Hund’s rule.
When we apply the Aufbau principle along with the Hund’s rule, we discover electron configurations for various atoms. Some of the atoms have partially filled shells (i.e., it has less electron than can fill up a complete \(n\) in the outermost shell). Some other atoms have an incompletely filled subshells (i.e., it has less electron than can fill up a complete \(l\) in the outermost shell). While some have completely shell and or subshell. These levels of filling explain the chemical similarities of elements in any one chemical group and give us a more complete picture of the reason for the arrangement of elements in the periodic table. The configurations of first ten elements obtained by successive filling of higher energy states are shown in Figure 52.79.
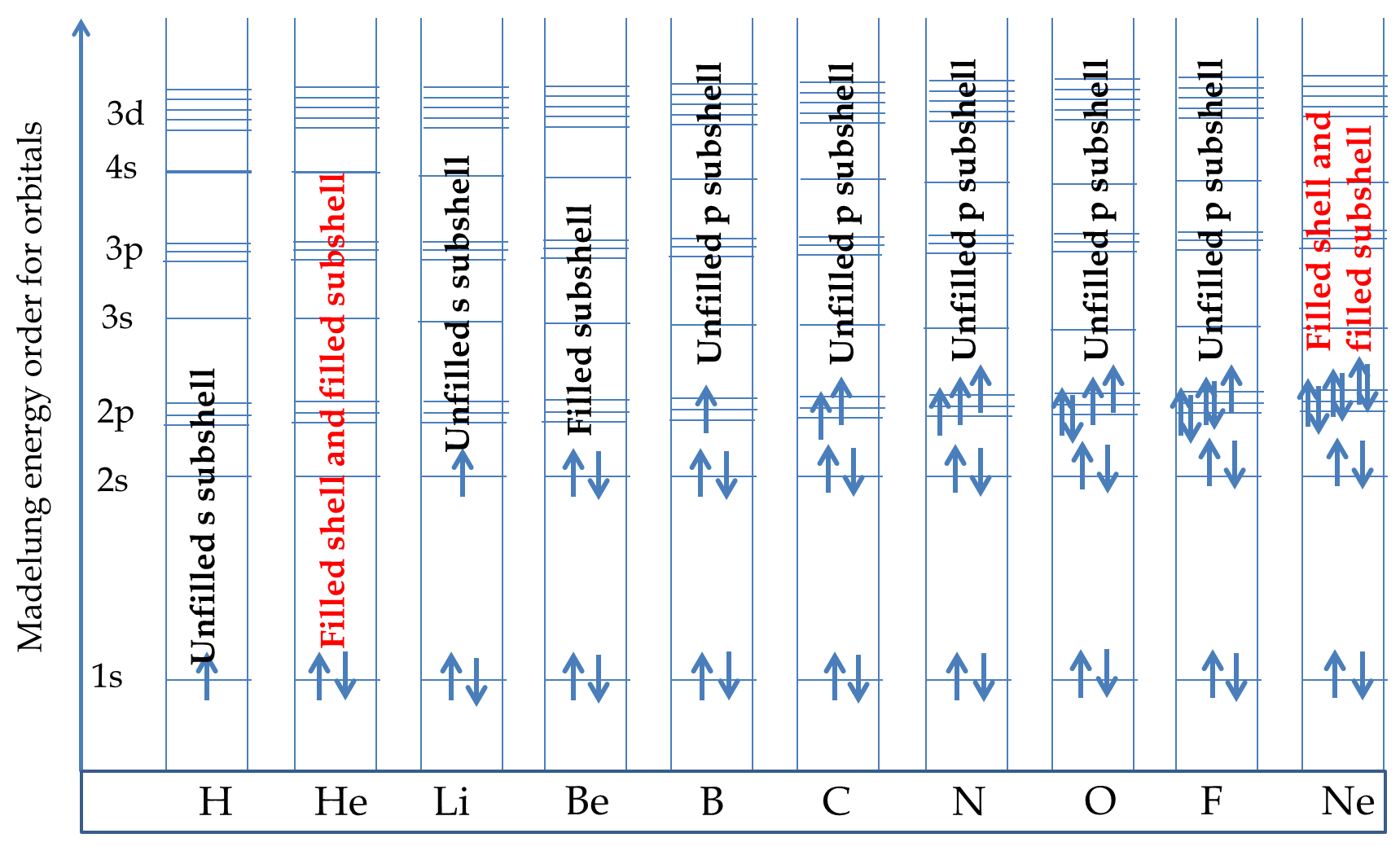
The electron configurations are written using the number \(n\) for the shell and letter \(s\text{,}\) \(p\text{,}\) \(d\text{,}\) \(f\text{,}\) \(g\text{,}\) etc, for the subshells \(l=0\text{,}\) \(1\text{,}\) \(2\text{,}\) \(3\text{,}\) \(4\text{,}\) \(5\text{,}\) respectively. When writing electron configurations, we omit the spin information and the Hund’s rule. Thus, the electron configurations of the first ten elements of the periodic table shown in Figure 52.79 are Table 52.80. Ground State Configurations Examples
A mystery of atoms is that as you add more protons in the nucleus the ionization energy does not keep rising. Instead, the ionization energy shows periodic behavior rising till the noble gases and then falling as shown in Figure 52.81. We can understand this periodic behavior on the basis of the electronic configuration obtained above. The ionization energy refers to the minimum energy necessary to knock an electron from the atom. Thus, this is the potential energy of the electron in the highest energy orbital occupied in an atom’s ground state.
| Element | Ground Configuration | Element | Ground Configuration |
|---|---|---|---|
| H | \(1s^1\) | C | \(1s^2 2s^1 2p^2\) |
| He | \(1s^2\) | N | \(1s^2 2s^1 2p^3\) |
| Li | \(1s^2 2s^1\) | O | 1s^2 2s^1 2p^4 |
| Be | \(1s^2 2s^2\) | F | 1s^2 2s^1 2p^5 |
| B | \(1s^2 2s^2 2p^1\) | Ne | 1s^2 2s^1 2p^6 |
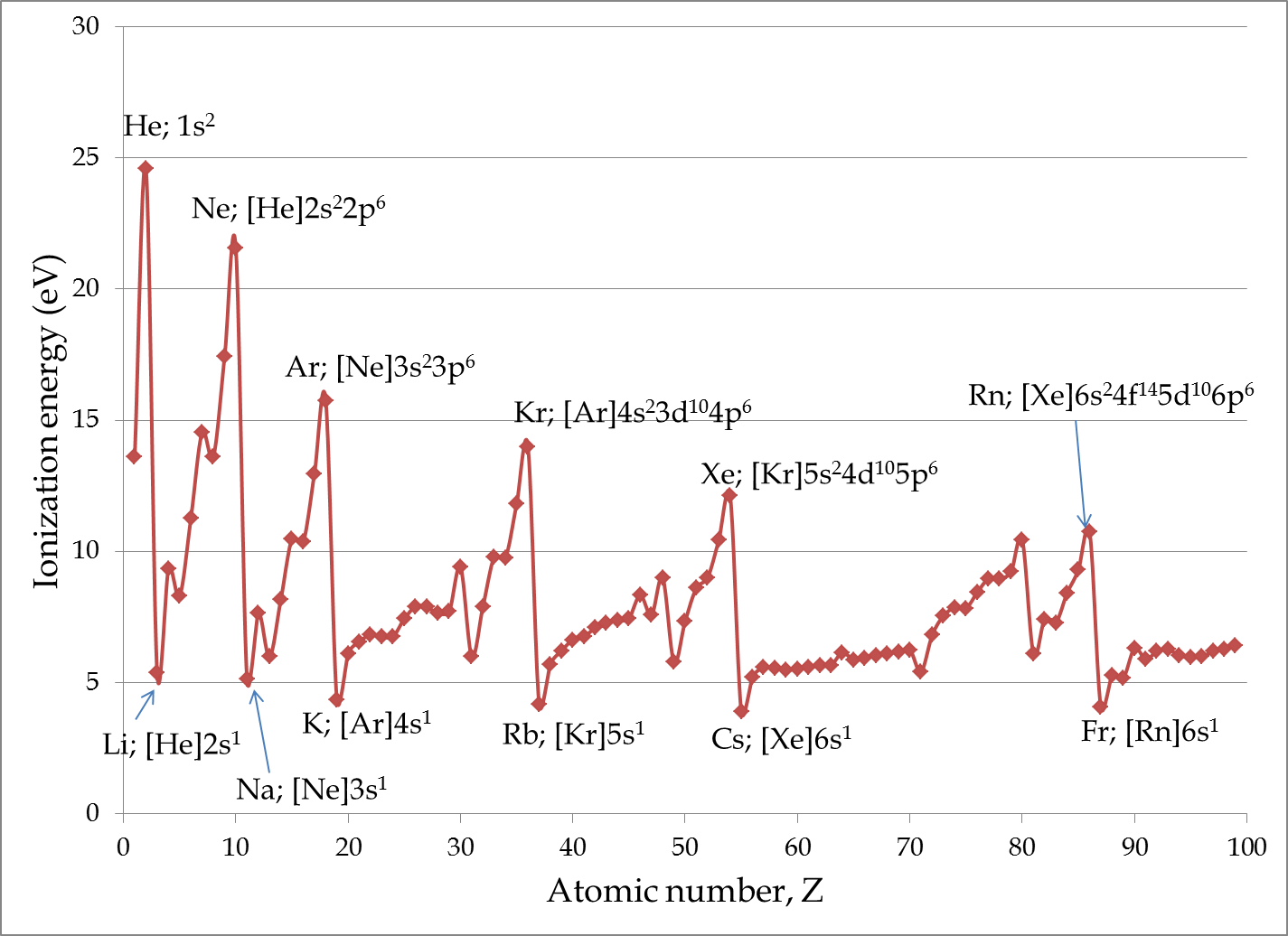
It is true that in a higher \(Z\) atom we have more protons in the nucleus, which would tend to pull the electrons closer to the nucleus. However, the electrons in the inner orbitals, the so-called core electrons, have a screening effect on the protons in the nucleus. The screening essentially has the effect of reducing the \(Z\) to a lower effective \(Z_{\textrm{effective}}\) making the nuclear charge less effective in binding the outer electrons. You can see this in a most pronounced way in the ionization energies of the alkali metals, Li, Na, K, Rb, Cs, and Fr. They act essentially as one-electron systems.

