Section 59.11 Dark Matter and Dark Energy
In 1933 Fritz Zwicky calculated the mass of the Coma Cluster by observing the motion of seven galaxies. If we know the speed \(v\) of a galaxy in a cluster and its distance \(r\) from the center of the cluster, then the mass \(M(r)\) within a distance \(r\) of the center can be shown to be
From his data Zwicky was able to determine the mass \(M_{cc}\) of the Coma Cluster. From the star count and the estimate of the masses of stars he also estimated the mass \(M_L\) in the luminous part of the Coma Cluster bu directly adding up the masses of the stars. To his surprise he found that the dynamically determined mass \(M_{cc}\) was 400 times the luminous mass \(M_L\text{.}\)
He called the missing mass the dark matter . With better measurements the amount of dark matter has been reduced but still the mass in the dark matter is far greater than the luminous mass. Initially, scientists did not pay much attention until in 1960s when Vera Rubin made more systematic and precise measurements of the rotation speeds of spiral galaxies. If a star is at a distance \(r\) from the center and moves with speed \(v\) then from Eq. (59.11.1) we expect the speed to obey the following equations:
where \(R\) is the radius of the galaxy and \(M(r)\) is the mass of the galaxy within a distance \(r\) from the center of the galaxy. The mass \(M(r)\) increases from 0 to \(R\) as more and more of the galaxy in included. Therefore, \(v\) increases as we go out from the center. However, once we are at the edge of the galaxy and outside the galaxy, \(M(R)\) is fixed and therefore, with increase in \(r\) we expect \(v\) to decrease with \(r\text{.}\) However, when Rubin plotted her data she found that the speeds did not go down as expected as if \(M(R)\) was keeping up with the increase in \(r\text{.}\) That is, there was an invisible mass that was having a gravitational effect on the star. A plot from literature of this effect is shown in Figure 59.11.1. It is estimated that more than 90\% of the mass in the universe is in the dark matter form.
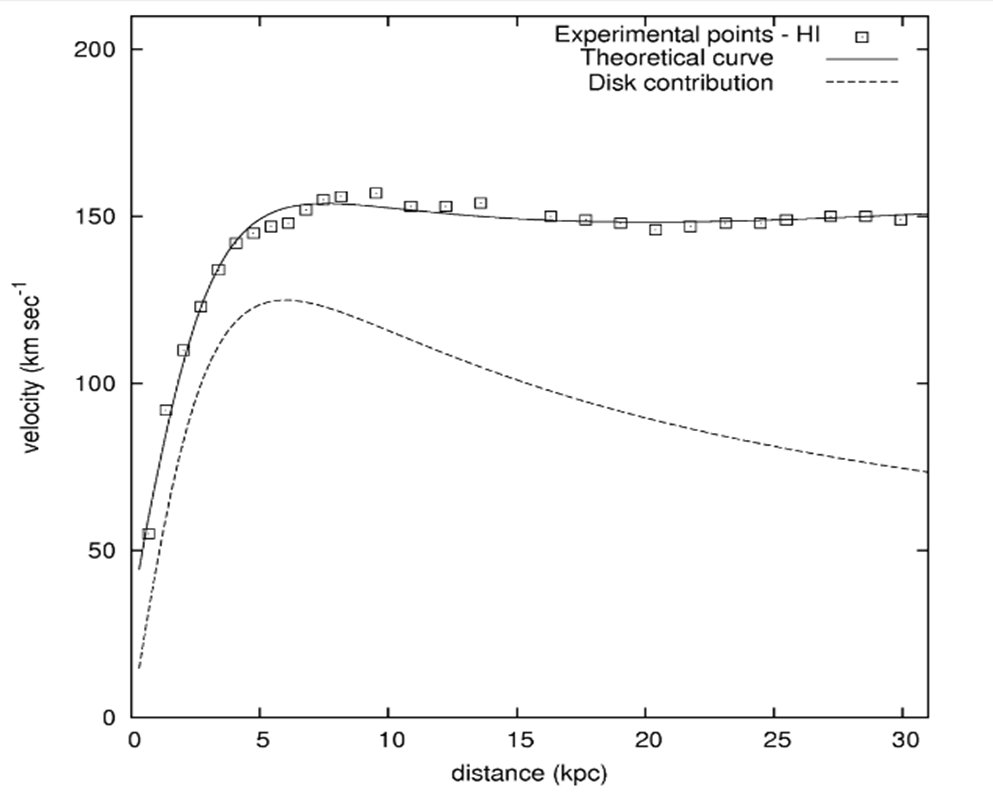
What is the dark matter composed of? At present it is a mystery. Several candidates of dark matter are in active research. The only clue so far is that dark matter interacts only weakly. Hypothetical particles such as WIMPs (Weakly Interacting Massive Particles) and MACHOs (Massive Compact Halo Objects) have been suggested.
Subsection 59.11.1 Critical Density
The expansion of the universe is slowed down by the gravitational pull of the matter on each other. If the universe has enough matter we expect the pull to decelerate the expansion and eventually collapse the universe. If the universe does not have enough matter, it may continue to expand forever. The critical density \(\rho_{\text{c}}\) is the density of matter in the universe at the boundary of these two possibilities. From Einstein's equation one can find an expression for \(\rho_{\text{c}}\) in terms of Newton's gravitational constant and Hubble's constant \(H_0\text{.}\)
With a standard value for \(H_0 = 70\:\text{km/s/Mpc}\) we get
where in the last step I have made the conversion of units from Mpc to m. Since the mass of one hydrogen atom is \(1.67 \times 10^{-27}\text{ kg}\text{,}\) the critical density corresponds to about \(5\) H atoms per cubic meter.
Subsection 59.11.2 Amount of Matter in the Universe
How does the density of the universe compare with the critical density? You might think that obtaining the density of the universe would be an impossible task. But it turns out that Astronomers have devised quite clever tricks to get a good estimate. One such method depends on counting galaxies, adding up their masses, and dividing the result by the volume containing them. It turns out that if you do this over large enough space, of the order of \(300\text{ Mpc}\) and higher, you get pretty uniform value regardless of the direction. A slice of \(5 \text{ Mpc} \times 5 \text{ Mpc}\) and a depth of \(300\text{ Mpc}\) sky will contain several thousand galaxies and is sufficient to give a good estimate. After surveying and counting is done, the luminous mass is estimated and then divided by the volume to obtain the luminous mass density, \(\rho_l\text{.}\) Normally, we divide the mass density by the critical density and report the mass density as a fraction of the critical density, denoted by the Greek letter \(\Omega\text{.}\) We will denote the \(\Omega\) from the luminous matter by \(\Omega_l\text{.}\)
Current observations show that \(\Omega_l = 0.002\ \text{to}\ 0.003\text{.}\) The dark matter is about 10 times this amount. Adding the dark matter contribution will give a total \(\Omega_{\text{matter}}\) to be
The luminous matter and dark matter add up to only 2 to 3\% of the critical density. Based on only this data, one would conclude that the universe does not have enough matter to stop the current expansion.
Subsection 59.11.3 Dark Energy and Acceleration of Universe
In 1990s it was observed that very far away galaxies have less redshifts than expected from Hubble's law. That would mean that the nearer galaxies have higher recession speed than these very farther ones. This implies that the universe is actually accelerating rather than decelerating, which is quite a surprise. After the big bang one would expect that the gravitational pull will tend to decelerate the expansion rate of space. The acceleration of the expansion can be understood if we introduce an energy term, called the dark energy, in Einstein's equation that would cause a repulsive force. It is indeed possible to introduce such a term, called the cosmological constant, in Einstein's equation. The amount of this additional energy required to explain the observation is quite high, almost three times the energy density from the matter. As is clear from the name, the subject of dark energy is very speculative and under intense study.