Physics Bootcamp

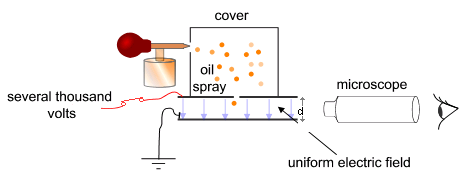
In 1909, American physicist Robert A. Millikan conducted experiments with charged oil drops. By balancing the electric and gravitational forces on oil drops, he was able to suspend them in mid-air (Figure 28.6.1). He found that the electric charges on oil drops were always integral multiples of a basic unit charge, thus establishing the quantization of charge.

The basic unit of charge is the same as the charge on one electron, and is denoted as usual by the letter \(e\text{.}\) In the SI system of units, the approximate value of \(e\) is \(1.6 \times 10^{-19}\ C\) as given above. The charge on one electron is \(-1\) times \(e\text{,}\) and the charge on a proton is \(+1\) times \(e\text{.}\) Since atoms have equal number of protons and electrons, they are neutral.

It is remarkable that the charge on a proton is exactly equal in magnitude to that of the charge on an electron, although the two particles differ in mass and many other properties. If the charges on electron and proton were slightly different from each other, the atom will have a net charge, and it will be impossible to make stable matter.

Not only is a proton's charge an integral multiple of \(e\text{,}\) but so are the charges on all other particles which can be isolated in nature. If we believe that matter is ultimately made up of elementary constituents, called elementary particles, then we only need to look at the charges on the elementary particles to verify the assertion of quantization of charge.

Presently the standard model of particle physics contains electron, muon, tau, electron-neutrino, mu-neutrino, tau-neutrino, up quark, down-quark, strange-quark, charm-quark, top-quark, bottom quark, \(W^+\text{,}\) \(W^-\text{,}\) \(Z\text{,}\) photon, Higgs particle and their anti-particles. All of these particles have zero, \(+e\) or \(-e\) of charge except for the quarks which have charges \(\pm \frac{2}{3}e\) and \(\pm \frac{1}{3}e\text{.}\)

Although, charges on quarks have been hypothesized to be a fraction of \(e\text{,}\) they have not been found in isolation. Instead, they reside inside other particles, e.g., a proton has two up quarks and a down quark and a neutron has two down quarks and an up quark. Every time an experiment is done with high enough energy that quarks could come out, one gets jets of particles that have integral multiples of charge \(e\text{.}\) The inability of experiments to knock individual quarks out of the composite particles has led to a belief that they may be permanently confined.