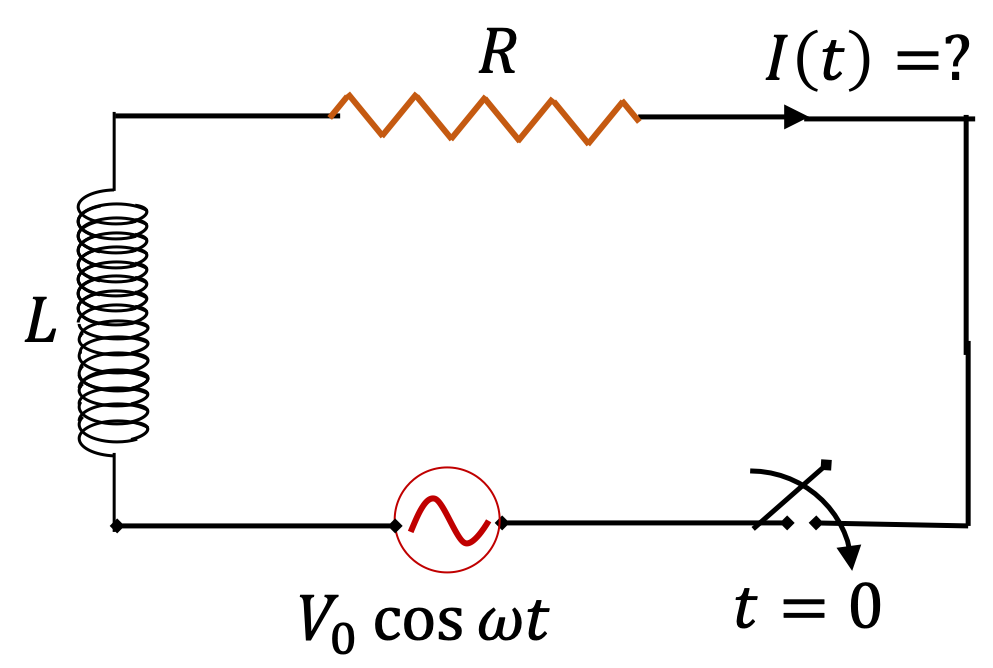
When switch is closed at
\(t=0\text{,}\) there is a transient behavior of the circuit, where the current in the circuit does not oscillate with the same frequency as the frequency of the driving EMF. But, after some time (here
\(t \gt \gt L/R \)) a steady state is reached, and thereafter, current in the circuit oscillates with the same frequency as the frequency of the driving EMF. Therefore, we can write the steady state solution of Eq.
(41.19) in the following form that has two unknowns the amplitude
\(I_0\) and phase constant
\(\phi_I\text{.}\)
\begin{equation}
I(t) = I_0\: \cos(\omega t+\phi_I).\ \ \ \text{(Steady state)} \tag{41.20}
\end{equation}
To find
\(I_0\) and
\(\phi_I\text{,}\) we substitute this solution in Eq.
(41.19) to obtain
\begin{equation*}
-L\:\omega\: I_0\: \sin(\omega t+\phi_I) + RI_0\: \cos(\omega t+\phi_I) = V_0\: \cos(\omega t).
\end{equation*}
Now, we expand the trigonometric functions and rearrange terms to obtain the following.
\begin{align*}
\amp \left[ V_0 + L\:\omega\: I_0\: \sin\phi_I - R\: I_0\: \cos\phi_I \right] \cos(\omega t)\\
\amp \ \ \ \ \ \ \ + \left[ L\:\omega\: I_0\: \cos\phi_I - R\: I_0\: \sin\phi_I \right] \sin(\omega t) = 0.
\end{align*}
In this equation, the coefficients of \(\cos(\omega t)\) and \(\sin(\omega t)\) must be independently zero since they are orthogonal functions. This can be shown by multiplying this equation by \(\cos(\omega t)\) and integrating over one period. You should do this step. you will find that this integration leads to the conclusion that the coefficient of the cosine term must be zero. Similarly, when you multiply by \(\sin(\omega t)\) and integrate over one period, you find that the coefficient of the sine term must be zero.
\begin{align}
\amp V_0 + L\:\omega\: I_0\: \sin\phi_I - R\: I_0\: \cos\phi_I = 0. \tag{41.21}\\
\amp L\:\omega\: I_0\: \cos\phi_I - R\: I_0\: \sin\phi_I = 0. \tag{41.22}
\end{align}
Therefore, we get the following for the phase constant of current
\begin{equation*}
\tan\phi_I = -\frac{\omega L}{R},
\end{equation*}
from which we get sine and cosine of \(\phi_I\text{.}\)
\begin{align*}
\amp \cos\phi_I = \frac{R}{\sqrt{R^2 +(\omega L)^2}}.\\
\amp \sin\phi_I = -\frac{\omega L}{\sqrt{R^2 +(\omega L)^2}}.
\end{align*}
Putting these expressions for
\(\sin\phi_I\) and
\(\cos\phi_I\) in Eq.
(41.21), we find
\(I_0\text{.}\)
\begin{equation*}
I_0 = \frac{V_0}{\sqrt{R^2 +(\omega L)^2}}
\end{equation*}
Summarizing, our results, we found current in the circuit is \(I=I_0\cos(\omega t + \phi_I)\) with
\begin{equation*}
I_0 = \frac{V_0}{\sqrt{R^2 +(\omega L)^2}},\ \ \ \ \phi_I = -\tan^{-1}\left(\frac{\omega L}{R}\right)
\end{equation*}