Example 29.14. Net Coulomb Force on a Charge by Two Other Charges on Cartesian Axes.
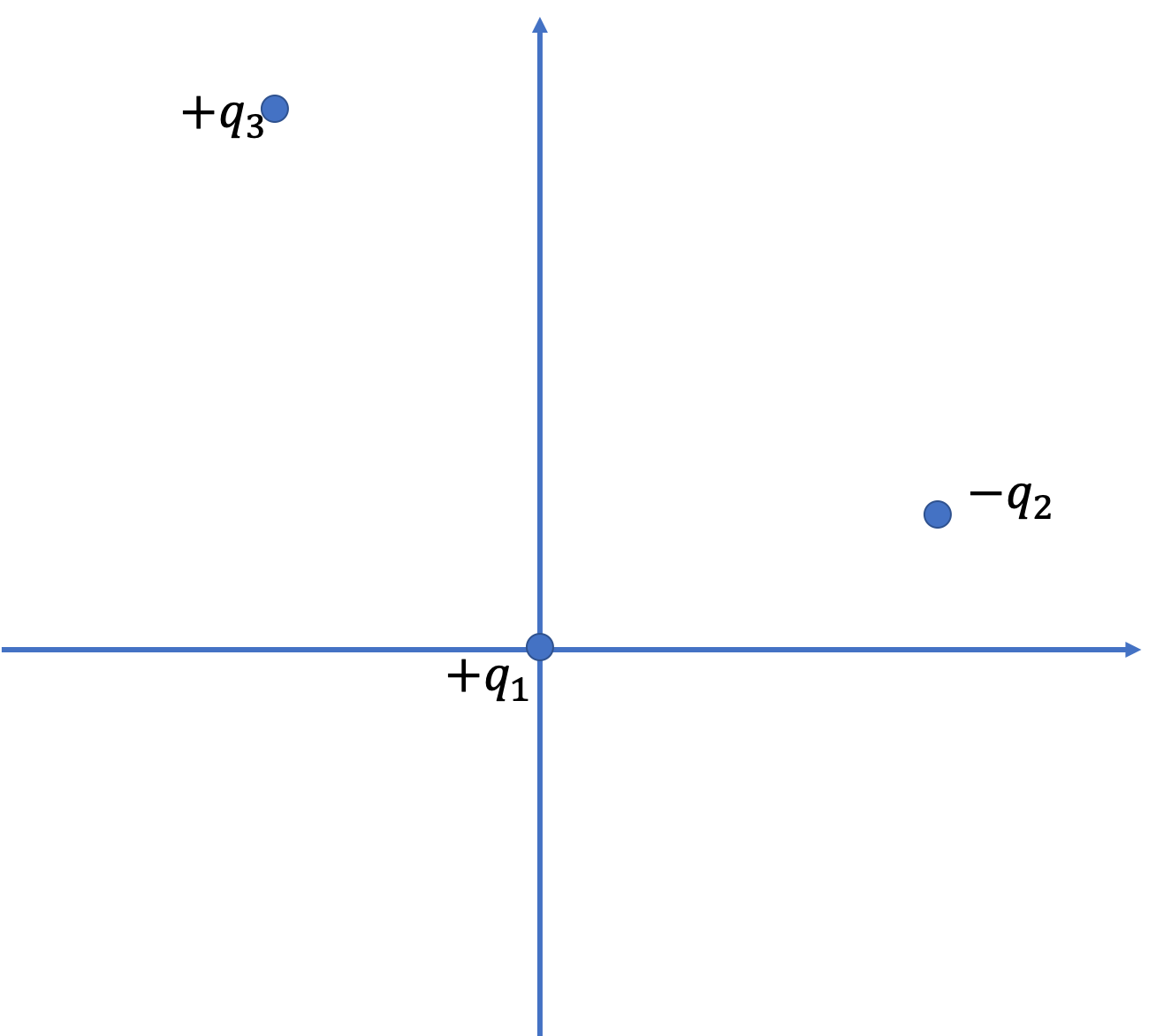
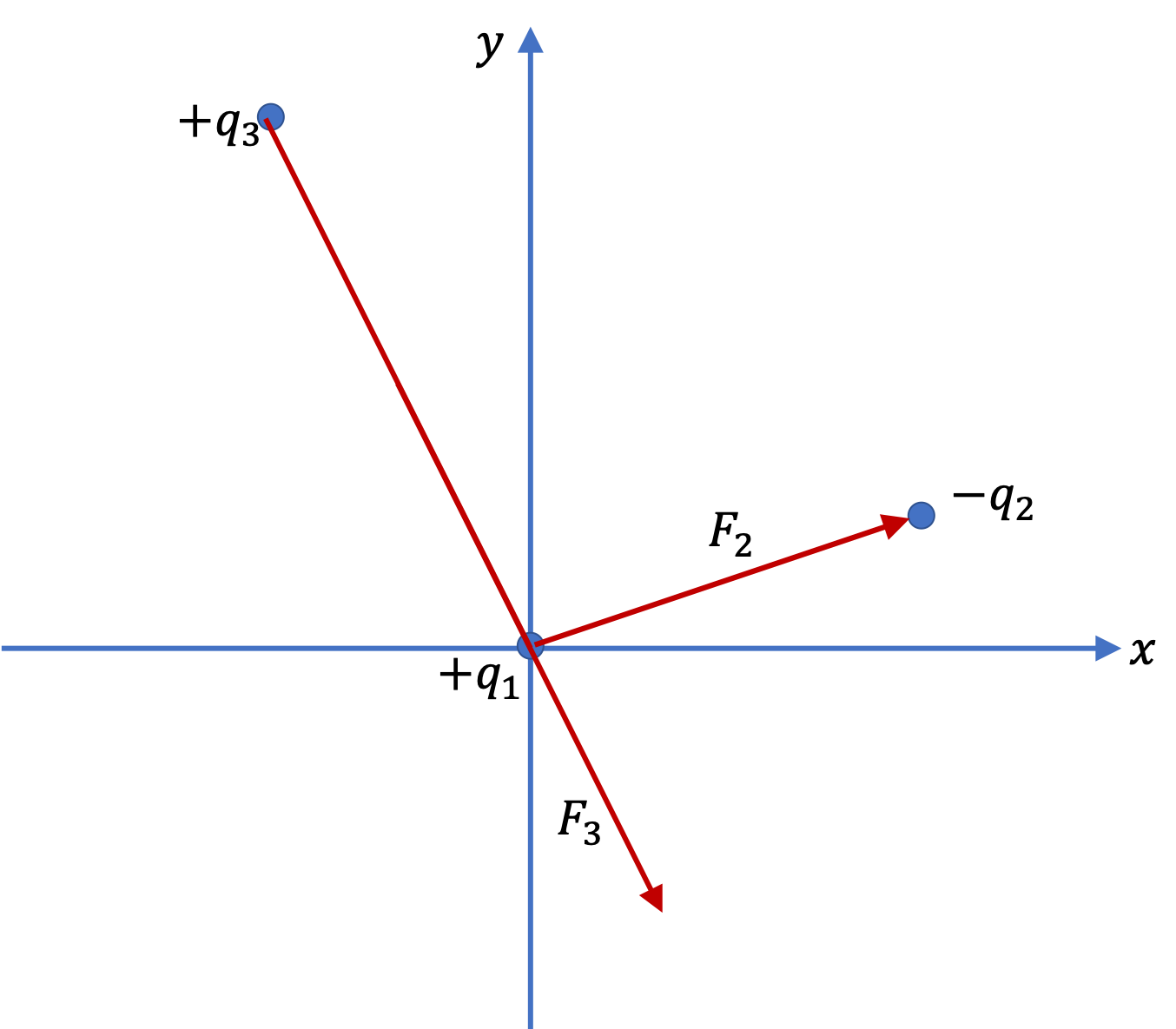
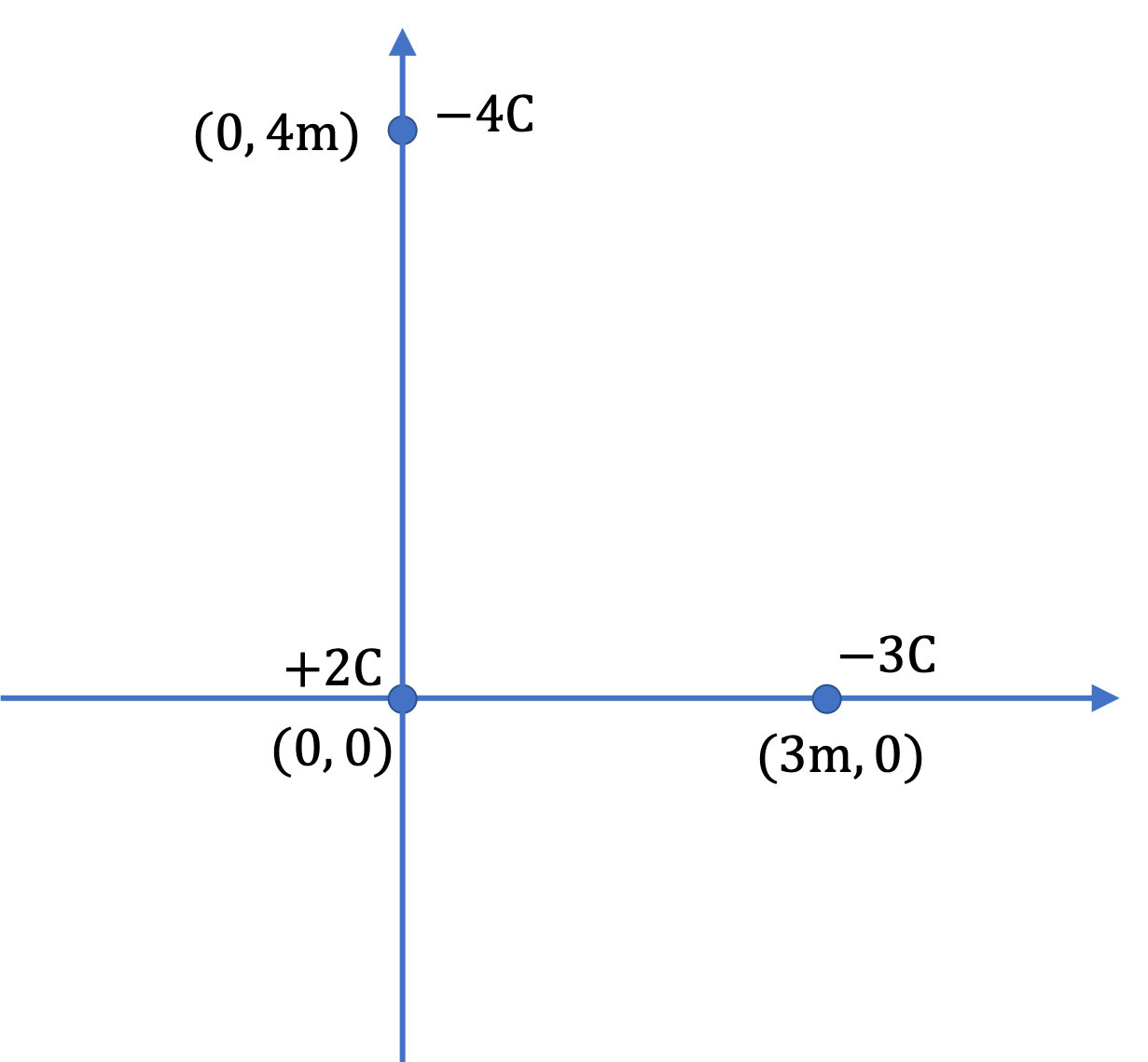
Find the force on the charge at the origin in the following system containing three charges.
Answer.
\(7.5\times 10^9\text{ N}\text{,}\) \(36.9^\circ\text{.}\)
Solution.
Let’s refer to the charge at the origin by subscript 1, the one on the \(x\) axis by 2, and the one on the \(y\) axis by 3. We need to vectorially sum the two forces \(F_2\) and \(F_3\) on the charge at the origin to get the magnitude and direction of the Coulomb force on charge 1.
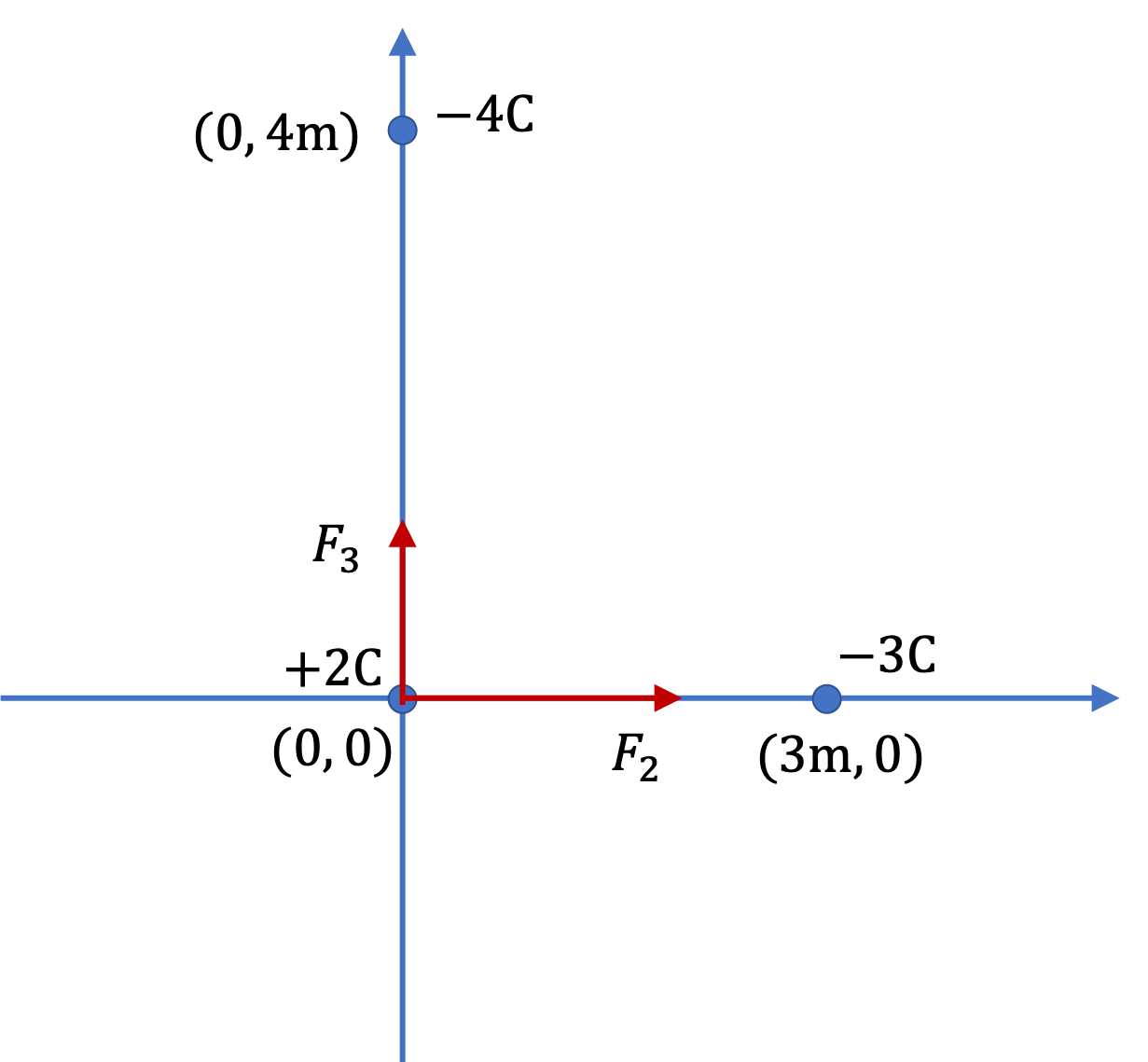
First we will work out the magnitudes of the two forces, and then, deduce their Cartesian components, which we will use to find the sum of the vectors. The magnitudes of the two forces are
\begin{align*}
F_2 \amp = k\dfrac{q_1 q2}{r_{12}^2} \\
\amp = 9\times 10^{9} \times \dfrac{2\times 3}{3^2} = 6\times 10^{9}\text{ N},\\
F_3 \amp = k\dfrac{q_1 q3}{r_{13}^2} \\
\amp = 9\times 10^{9} \times \dfrac{2\times 4}{4^2} = 4.5\times 10^{9}\text{ N}.
\end{align*}
To add these forces, we can’t just add the magnitudes. Since they are in perpendicular directions, Pythagora’s theorem will give us an easy way to get the magnitude. Let \(F\) denote the magnitude of the net force. We can notice that its \(x\) and \(y\) components are simply
\begin{gather*}
F_x = F_{2x}+F_{3x} = 6\times 10^{9}\text{ N}+0,\\
F_y = F_{2y}+F_{3y} = 0+4.5\times 10^{9}\text{ N}.
\end{gather*}
Therefore, the magnitude will be
\begin{equation*}
F = \sqrt{ F_x^2 + F_y^2 } = \sqrt{ 6^2 + 4.5^2 }\times 10^9 = 7.5\times 10^9\text{ N}.
\end{equation*}
and the direction can be given by the counterclockwise angle from the positive \(x\) axis since point \((6,\ 4.5)\) is in the first quadrant.
\begin{equation*}
\theta = \tan^{-1} \left( \dfrac{4.5}{6} \right) = 36.9^\circ.
\end{equation*}