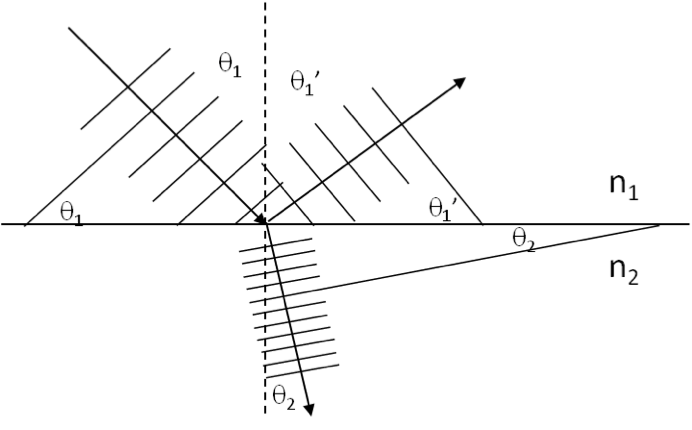
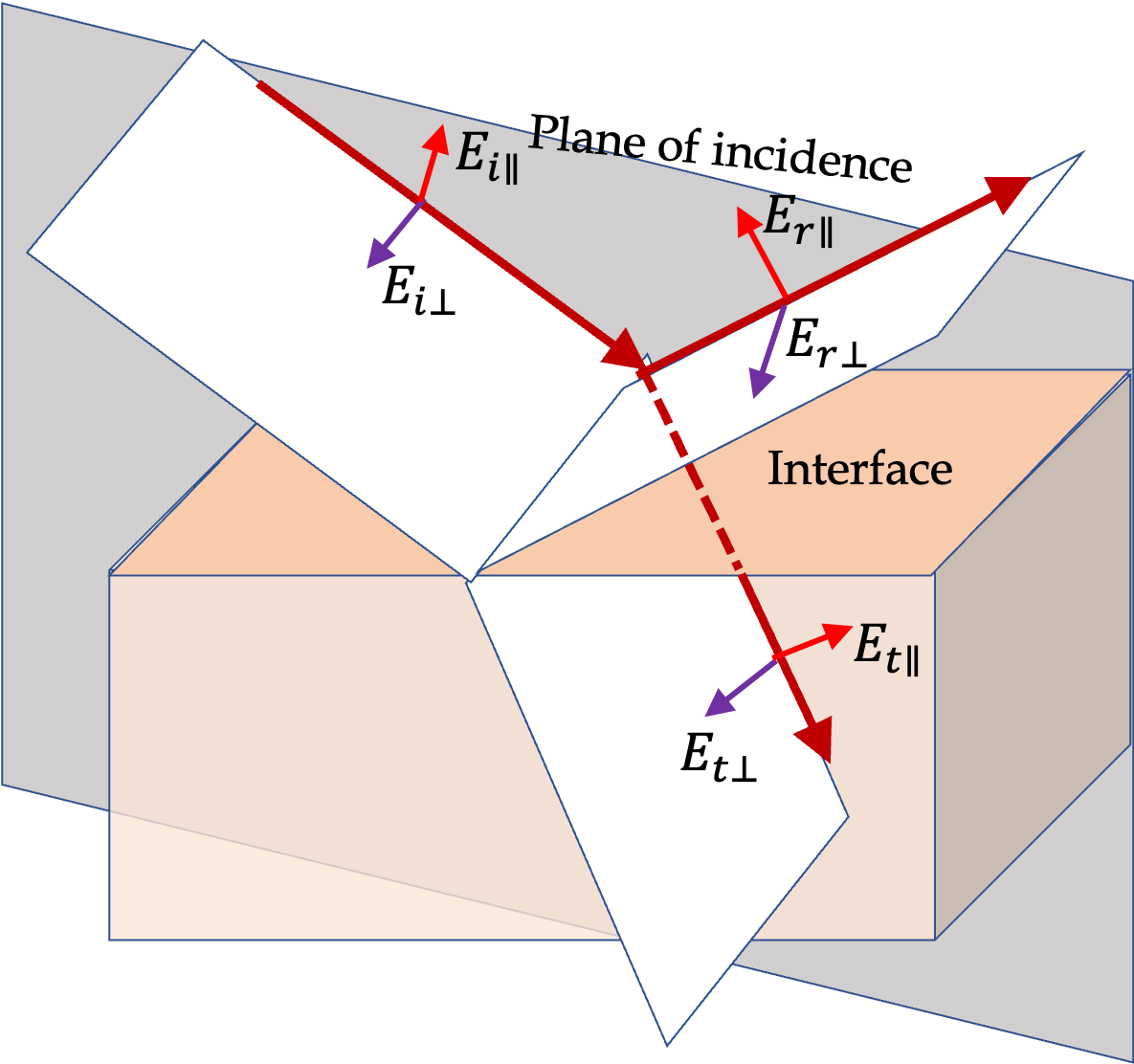
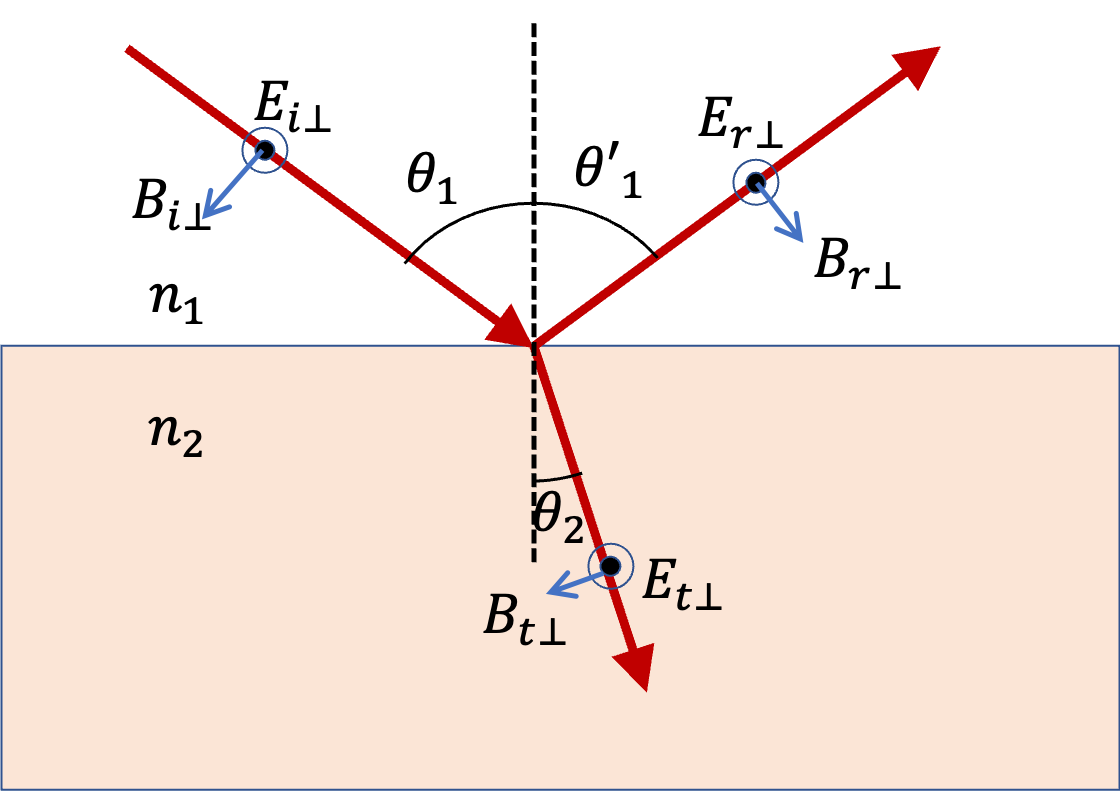
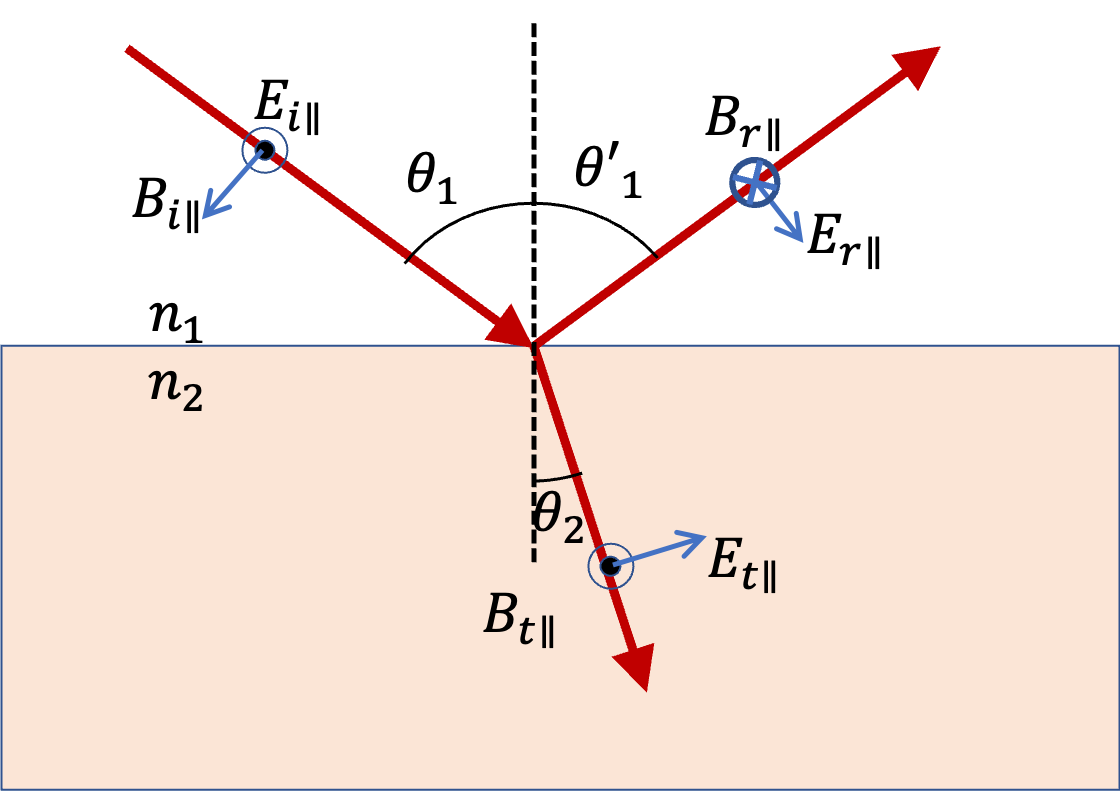
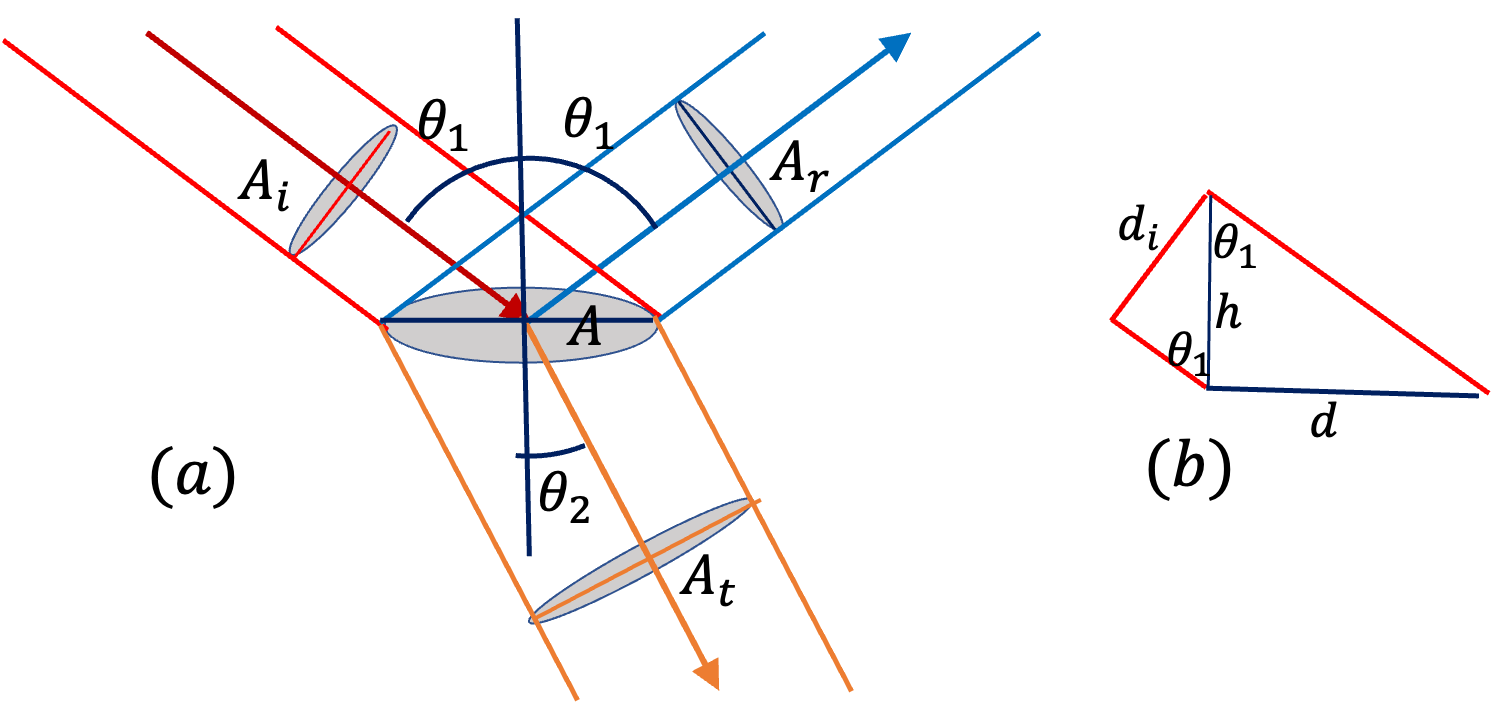
Figure 46.14(a) shows incident,reflected, and transmitted beams with area
\(A\) at the interface and the corresponding cross-sectional areas of the beams
\(A_i\text{,}\) \(A_r\text{,}\) and
\(A_t\text{.}\) From the geometry of the incident beam shown in figure (b), you can show that
\begin{equation*}
A_i = A\cos\theta_1.
\end{equation*}
Similarly, for other beams we will get
\begin{equation*}
A_r = A\cos\theta_1,\ \ A_t = A\cos\theta_2.
\end{equation*}
Now power in each beam will be related to their areas of cross-sections. Let \(I_i\text{,}\) \(I_r\text{,}\) and \(I_t\) be the intensities of the three beams. Recall that intensity in an electromagnetic wave is given by
\begin{equation*}
I = \frac{1}{2}\epsilon v E_0^2,
\end{equation*}
where \(\epsilon \) is the electric susceptibility of the medium, \(v\) the speed of light in that medium, and \(E_0\) the electric field amplitude of the EM wave. We can write the constant factors multiplying the square of the amplitude by using \(\epsilon=n^2\) and \(v=c/n\) and get the following useful expression of intensity, which we will use below.
\begin{equation}
I = \frac{c}{2} n E_0^2.\tag{46.39}
\end{equation}
Since intensity is power per unit area, power in each beam will be
\begin{equation*}
P_i = I_i A_i,\ \ P_r = I_r A_r,\ \ P_t = I_t A_t.
\end{equation*}
From energy conservation, we expect that
\begin{equation}
P_r + P_t = P_i\tag{46.40}
\end{equation}
Dividing both sides by \(P_i\) can remove the need to “know” the area of cross-section.
\begin{equation}
\frac{P_r}{P_i} + \frac{P_t}{P_i} = 1.\tag{46.41}
\end{equation}
These ratios are called reflectance and transmittance. They are denoted by \(R\) and \(T\text{,}\) respectively.
\begin{align}
\amp \text{Reflectance, } R = \frac{P_r}{ P_i} = \frac{I_r}{I_i}.\tag{46.42}\\
\amp \text{Transmitance, } T = \frac{P_t}{ P_i} = \frac{I_t \cos\theta_2}{I_i \cos\theta_1}.\tag{46.43}
\end{align}
Rewriting Eq.
(46.41), we find that energy conservation in the reflection/refraction of an incident beam then takes a simple form.
\begin{equation}
R + T = 1.\tag{46.44}
\end{equation}
By expressing \(R\) and \(T\) in terms of intensities and then replacing intensities, we can write \(R\) and \(T\) in terms of reflection and transmission coefficients, \(\rho\) and \(\tau\text{.}\)
\begin{align*}
R \amp = \frac{I_r}{I_i} = \frac{\frac{c}{2} n_1 E_{0r}^2}{\frac{c}{2} n_1 E_{0i}^2} = \rho^2. \\
T \amp = \frac{I_t\cos\theta_2}{I_i\cos\theta_1} = \frac{\frac{c}{2} n_2 E_{0t}^2 \cos\theta_2}{\frac{c}{2} n_1 E_{0i}^2 \cos\theta_1} = \frac{n_2\cos\theta_2}{n_1\cos\theta_1}\ \tau^2.
\end{align*}
Let’s first verify for S-polarization. Using
\(\rho\) and
\(\tau\) from Eqs.
(46.32) and
(46.33), we get
\begin{align*}
R + T \amp = \rho^2 + \frac{n_2\cos\theta_2}{n_1\cos\theta_1}\ \tau^2 \\
\amp = \left( \frac{n_1\cos\theta_1 - n_2\cos\theta_2}{n_1\cos\theta_1 + n_2\cos\theta_2} \right)^2\\
\amp \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \frac{n_2\cos\theta_2}{n_1\cos\theta_1} \left( \frac{2n_1\cos\theta_1}{ n_1\cos\theta_1 + n_2\cos\theta_2 }\right)^2\\
\amp = \frac{(n_1\cos\theta_1 - n_2\cos\theta_2 )^2 + 4n_1n_2\cos\theta_1\cos\theta_2 }{ (n_1\cos\theta_1 + n_2\cos\theta_2 )^2} = 1.
\end{align*}
How about for the P-polarization? Using
\(\rho\) and
\(\tau\) from Eqs.
(46.34) and
(46.35), we get
\begin{align*}
R + T \amp = \rho^2 + \frac{n_2\cos\theta_2}{n_1\cos\theta_1}\ \tau^2 \\
\amp = \left( \frac{n_1\cos\theta_2 - n_2\cos\theta_1}{n_1\cos\theta_2 + n_2\cos\theta_1} \right)^2\\
\amp \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \frac{n_2\cos\theta_2}{n_1\cos\theta_1} \left( \frac{2n_1\cos\theta_1}{ n_1\cos\theta_2 + n_2\cos\theta_1 }\right)^2\\
\amp = \frac{(n_1\cos\theta_2 - n_2\cos\theta_1 )^2 + 4n_1n_2\cos\theta_1\cos\theta_2 }{ (n_1\cos\theta_2 + n_2\cos\theta_1 )^2} = 1.
\end{align*}