Magnetic Field of Magnets

Section 40.5 Magnetic Field of Magnets

Previously we have studied magnetic field by steady electric current as given by Biot-Savart law and Ampere's law. We study magnetic field of magnets mostly empirically by experiments. However, the current-loop equivalence of a magnetic dipole provides a way to study magnets theoretically as well.

For instance, to know the magnetic field of a tiny magnet at a point along the dipole, we just work out the magnetic field at the axis of a loop of current. Then, we substitute \(\mu\) for \(IA\) and take a limit where size of the loop becomes small. For a dipole \(\mu\) pointed towards \(z\) axis, we get magnetic field at a point on the \(z\) axis to be

\begin{equation} \vec B_P = \dfrac{\mu_0}{2\pi}\dfrac{\mu}{z^3}\, \hat u_z.\label{eq-dipole-field-at-axis}\tag{40.5.1} \end{equation}

Magnetic field of a magnetic dipole at a point that is not on the axis is more difficult to work out.

Here we will just cite the formula for magnetic field at a point P that is located at a spherical radial distance \(r\) from the origin and line from origin to P makes an angle \(\theta\) with respect to \(z\) axis for a magnetic dipole placed at the origin in the \(z\) axis direction.

\begin{equation} \vec B_P = \dfrac{\mu_0\mu}{4\pi r^3}\left( 2\cos\theta\ \hat u_r + \sin\theta\ \hat u_{\theta}\right).\label{eq-dipole-field-at-arbitrary-point}\tag{40.5.2} \end{equation}

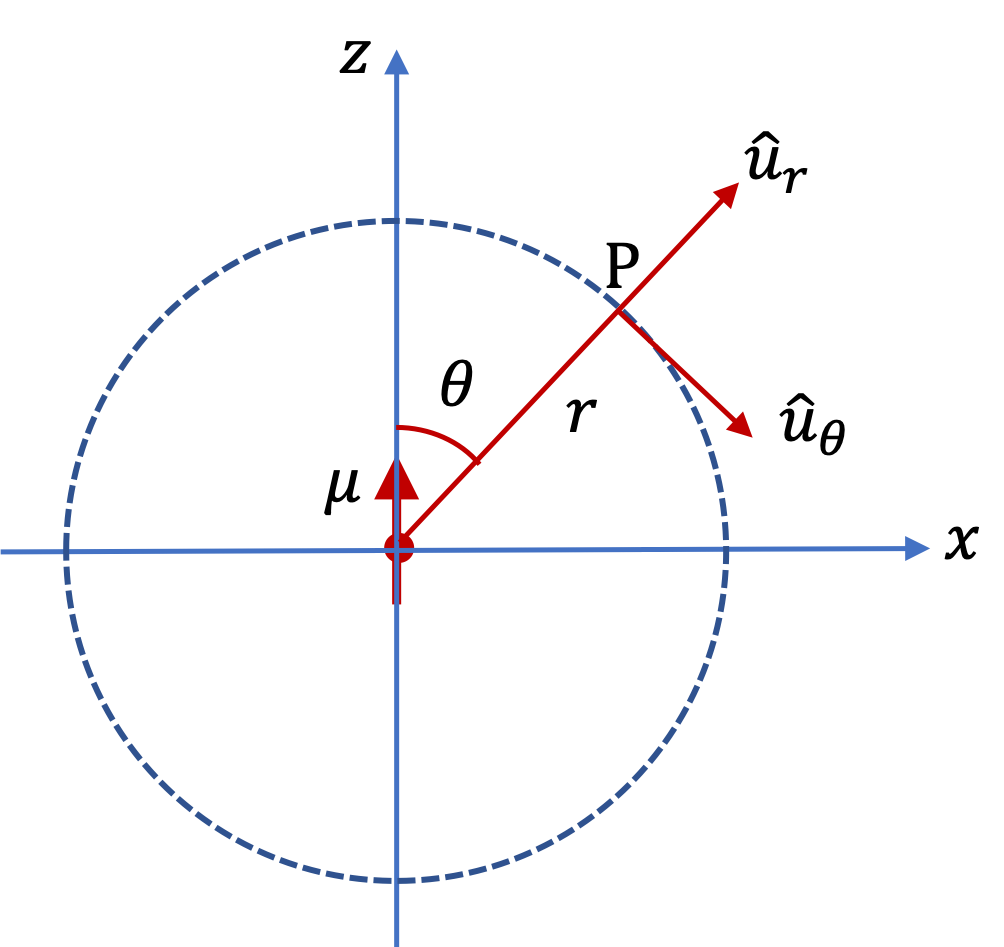
In this formula \(\hat u_r\) and \(\hat u_\theta \) are radial unit vector and a unit vector tangent to the great circle through P. This field is called dipole field due to its distance dependence of \(1/r^3\text{.}\)

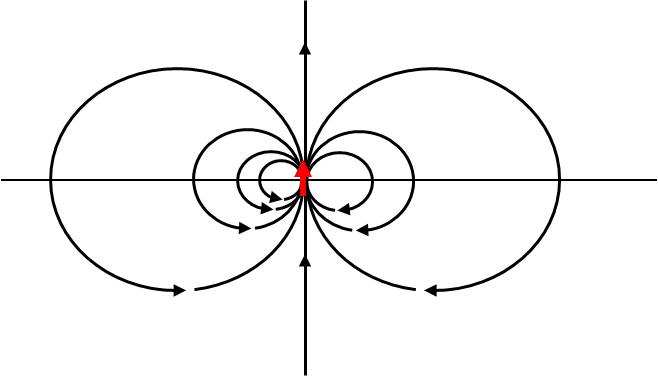
The dipole field is symmetric about the direction of the dipole - you get the same picture when you rotate about the direction of the dipole. Therefore, we can just draw field lines in \(xz\) plane as shown in Figure 40.5.3. You can rotate the field lines in your mind to figure out what it would look like in three dimensional space.

Figure 40.5.3. Magnetic dipole field lines of a magnetic dipole.

Subsection 40.5.1 (Calculus) A Uniformly Magnetized Thin Bar Magnet

To figure out magnetic field around a thin bar magnet, we can superpose the magnetic field by each piece of the thin bar. To be specific, consider a bar magnet of length \(L\text{,}\) which is unifomly magnetized in the direction of its length with magnetic dipole moment per unit length equal to \(M\text{.}\)

Let bar be placed along the \(z\) axis with its magnetization pointed in the positive \(z\) direction. We will find magnetic field from this magnet at a point on the \(z\) axis that is far away from the magnet and on the positive \(z\) axis.

Using Eq. (40.5.1) we can write the field by the piece of bar between \(z'\) and \(z'+dz'\text{.}\) Note that \(z\) in the formula in Eq. (40.5.1) is the distance from the dipole at origin. Therefore, we will need to replace \(z\) there by \(z-z'\text{.}\) The dipole moment in \(dz'\) is \(d\mu = Mdz'\text{.}\) Therefore, \(z\) component of the field at P is

\begin{align*} dB_z \amp = \dfrac{\mu_0}{2\pi}\dfrac{d\mu}{(z-z')^3}\\ \amp = \dfrac{\mu_0}{2\pi}\dfrac{ Mdz'}{(z-z')^3} \end{align*}

We will integrate this from \(z'=-L/2\) to \(z'=L/2\) to get the net field at P.

\begin{align*} B_z \amp = \dfrac{\mu_0 M }{2\pi} \int_{-L/2}^{L/2}\, \dfrac{ dz'}{(z-z')^3} \\ \amp = \dfrac{\mu_0 M }{2\pi} \left[ \dfrac{1}{2(z-z')^2} \right]_{-L/2}^{L/2} \\ \amp = \dfrac{\mu_0M}{\pi}\left[ \dfrac{1}{\left(2z-L \right)^2} - \dfrac{1}{\left(2z+L \right)^2} \right]. \end{align*}

Note that this formula is only good for point on the axis. The magnetic field at an arbitray point will be different from this formula.

Subsection 40.5.2 (Calculus) A Uniformly Magnetized Sphere

Consider a sphere of radius R that is uniformly magnetized with magnetization \(M\text{.}\) We choose \(z\) axis to be the direction of the magnetization and use a spherical coordinate to write the answer here. Let \(m\) denote the total dipole moment of the sphere, i.e.,

\begin{equation*} m = \dfrac{4}{3}\pi R^3 M. \end{equation*}

I will not give a derivation of the results. Instead, I will just quote the results and let it a challenge to a more ambitious student to prove them. The magnetic field at a distance \(r\) from the center of the sphere and at an angle \(\theta\) from the direction of the dipole is given by the following formula in spherical coordinates.

\begin{equation*} \vec B(r,\theta,\phi) = \left\{ \begin{array}{ll} \dfrac{2}{3}\mu_0 M\, \hat k\amp\ \ \ \ (r\lt R)\\ \dfrac{\mu_0}{4\pi}\dfrac{m}{r^3}\left( 2\cos\theta\,\hat u_r + \sin\theta\,\hat u_{\theta}\right) \amp\ \ \ \ (r \gt R) \end{array} \right. \end{equation*}

The magnetic field outside is that of the total magnetic moment placed at the center of the sphere.