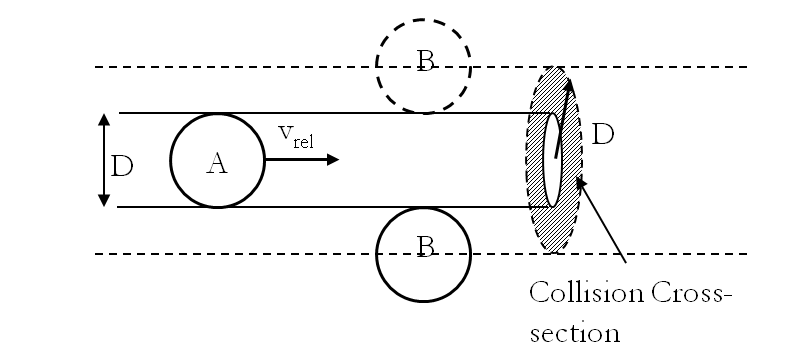
Unlike ideal gases the molecules of real gases interact with each other and collide which changes their momenta. The average distance traveled by a molecule between collisions is called the mean free path. To get a useful estimate of the
mean free path, we model molecules as spheres of diameter
\(d\text{,}\) and look at the collision cross-section between two molecules
\(A\) and
\(B\) as shown in
Figure 27.10, which is drawn in the rest frame of
\(B\text{.}\) Let
\(v_{rel}\) be average relative speed between two molecules.
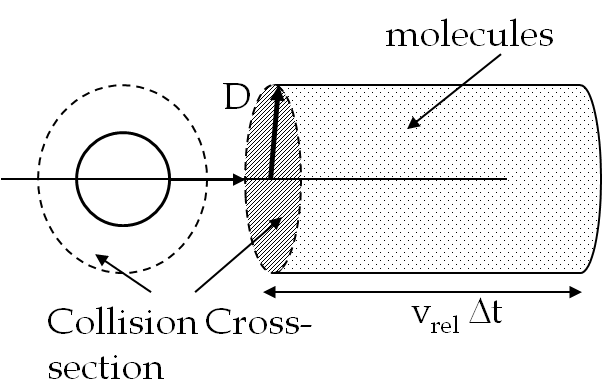
The number of collisions suffered by a molecule will depend on the density of molecules and their relative speed. Although after each collision the direction of motion of a molecule will change, but in each direction it is the same cross-sectional area. Therefore the number of collisions in some duration
\(\Delta t\) will equal the number of molecules in the volume of a cylinder of the cross-sectional area
\(\pi D^2\) and length
\(v_{rel} \Delta t\text{,}\) the distance traveled by the molecule shown as A (
Figure 27.11).
\begin{align*}
\amp \text{Number of collisions in } \Delta t = \dfrac{N}{V}\left(\pi D^2 v_{rel}\Delta t \right)\\
\amp \text{Distance traveled in } \Delta t = v_\text{ave} \Delta t
\end{align*}
where \(v_\text{ave}\) is the average speed of the molecule, \(N\) is the total number of molecules occupying volume \(V\text{.}\) It can be shown that the average speed is related to the average relative speed as follows.
\begin{equation*}
v_{rel} = \dfrac{ v_\text{ave} }{\sqrt{2}}
\end{equation*}
Hence, mean free path \(\lambda\) is
\begin{equation*}
\text{Mean free path, }\lambda = \dfrac{\text{Distance traveled}}{\text{Number of Collisions}} = \dfrac{1}{\sqrt{2}\ \pi D^2}\dfrac{V}{N}.
\end{equation*}
Because most real gases at high temperature and low density behave as ideal gas, sometimes we can use the ideal gas law even for real gases. In that case we can replace \(V/N\) and obtain mean free path in terms of temperature and pressure.
\begin{align*}
\text{Approximately Ideal}\text{ Gas} \amp \text{ Behavior:} \lambda = \dfrac{k_B}{\sqrt{2}\ \pi D^2}\dfrac{T}{p}.
\end{align*}
You might call this “ideal gas mean free path”. In a strict sense, a true ideal gas will have \(\lambda = \infty\text{,}\) since the molecules of an ideal gas do not interact with each other. This formula is a mixture of ideas from the real gas and the ideal gas and the final mean free path formula is often called the “ideal gas mean free path”.