Section 58.2 The Fundamental Forces
In everyday experience, physical objects interact with each other by several different types of forces. For instance, when a person pushing on a table we say that the person is applying a push force on the table, when Earth pulls on a skydiver we say that there is a force of gravity on the skydiver, when two friends are pulling on each other by pulling on a rope we say that there is a tension force on the them, and so on. It turns out that all of these myriads of forces are actually manifestations of only four fundamental forces:
- Gravitational force. This is a universal interaction between all objects, large or small, and is the weakest of all. There is no limitation to the distance beyond which the gravitational force stops to act. Gravitational force is a long-range force.
- Electric and magnetic forces. Electric and magnetic forces appear to be two different types of forces, but James Clerk Maxwell showed that these two forces are different manifestations of the same force. The electromagnetic interaction between two objects occurs when they are electrically charged and also between a charged body and electromagnetic radiation or photon. For the same charged particles at the same distance, electromagnetic force is much stronger than the gravitational force. The electromagnetic force is also a long-range interaction.
- Weak force. The weak force is a very short-range force, being effective only within a distance less than \(10^{-3}\) fm, i.e., within a nucleon. The beta decay of nuclei is due to the weak interaction. In the 1960s and 1970s, a unified theory of electromagnetic and weak interactions was developed which has been verified experimentally. The new interaction is called electroweak interaction. The theory showed that, although electromagnetic and weak forces appear very different at everyday low energies, they would merge into a single electroweak force above the unification energy, which is on the order of 100 GeV.
- Strong force. Historically, the strong force refers to the force between nucleons, protons and neutrons, in a nucleus that helps explain the binding of nucleons despite very strong repulsive force between protons. In the modern time, the strong force between nucleons is though to arise from even more fundamental force between quarks. Quarks are constituents of nucleons and other hadrons, which we will study later in this chapter. The fundamental force between quarks is the color force. We will use the same name - strong force - for both the fundamental strong force and the effective strong force.
Subsection 58.2.1 Force Carriers
In the field picture of forces, we envision space to be filled with a force field. We understand the force on a particle by the effect of the force field on the particle. For instance, a charge \(q\) will experience a force \(\vec F\) if there is an electric field \(\vec E\) at the location of the charge.
In this view, the force between two charges \(q_1\) and \(q_2\) is described by electric fields \(\vec E_1\) and \(\vec E_2\) created by the two charges. The force on \(q_1\) will be
and the force on \(q_1\) will be
Treating forces by using force field is quite adequate for classical physics, i.e. non-quantum physics. The relativistic quantum physics, called quantum field theory (QFT), has introduced a different view of how two particles interact with each other. In QFT, one of the interacting particle emits a force mediator particle, which is then absorbed by the other particle, creating an interaction between the emitting particle and the absorbing particle.
For instance, the electric force between two electrons occurs when one electron emits a photon which is subsequently absorbed by the second electron. A diagram, called the Feynman Diagram, helps visualize the interaction process. Two Feynman diagrams for electromagnetic interaction (a) between electron and electron and (b) between electron and proton are illustrated in Figure 58.2.1. In the quantum picture of interaction, a force between particles occurs through exchanging force particles.
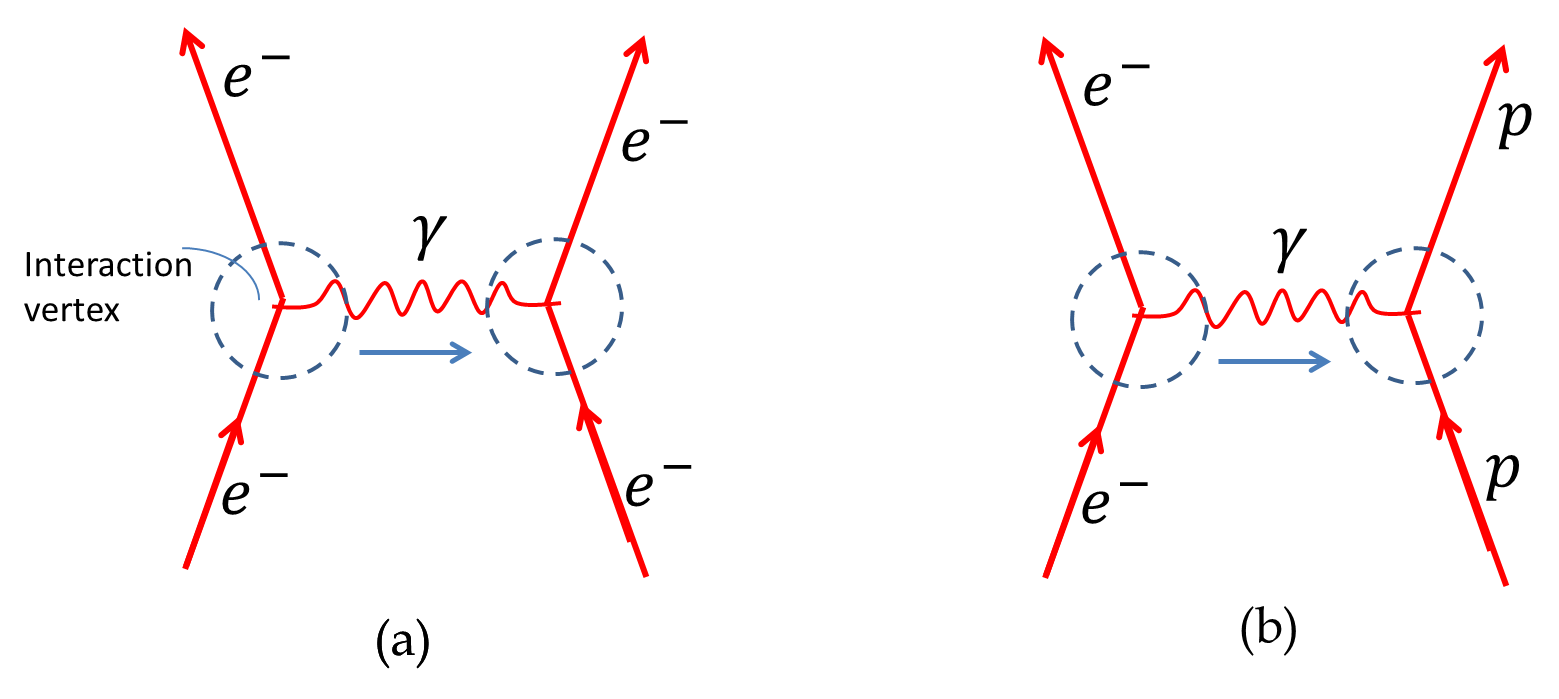
Every force is therefore mediated by one or more field particle(s) corresponding to the force. Table 58.2.2 displays the force carriers for the four fundamental forces and some important characteristics of each force. There is one field particle for electromagnetic force, three field particles for the weak force, eight for the strong force, and one proposed for gravity. These force-mediating particles are often called gauge bosons.
| Force | Range of force | Relative strength | Force carrier |
|---|---|---|---|
| Gravitation | Long | 1 | Graviton (proposed) |
| Electromagnetic | Long | \(10^{41}\) | Photon |
| Weak | Very short, \(\approx 10^{-3}\) fm | \(10^{37}\) | W\(^{+}\text{,}\) W\(^{-}\text{,}\) Z\(^{0}\) |
| Strong/Color | Short, \(\approx 1\) fm | \(10^{43}\) | Gluons (8 types) |
Subsubsection 58.2.1.1 Yukawa Potential
We can illustrate characteristics of force mediators by the treatment of effective strong force between nucleons due to Hideki Yukawa of Japan. Yukawa proposed the following potential \(U(r)\) for the attractive force between nucleons
where \(r_0\) is a parameter with units of length, and \(k\) is a constant signifying the strength of the interaction. If you plot this potential versus \(r\) you will find that the potential decreases to zero more rapidly for smaller \(r_0\) and less rapidly with larger \(r_0\text{.}\) That is, the parameter \(r_0\) is a measure of the range of force.
Yukawa showed that if the range \(r_0\) will be related to the rest mass \(m\) of the force carrier.
Suppose that \(r_0\) was equal to the de Broglie length of the particle if the particle had a speed close to the speed of light. The, our guess will be
Let us calculate the mass of the force carrier whose range is 10 fm. This will give
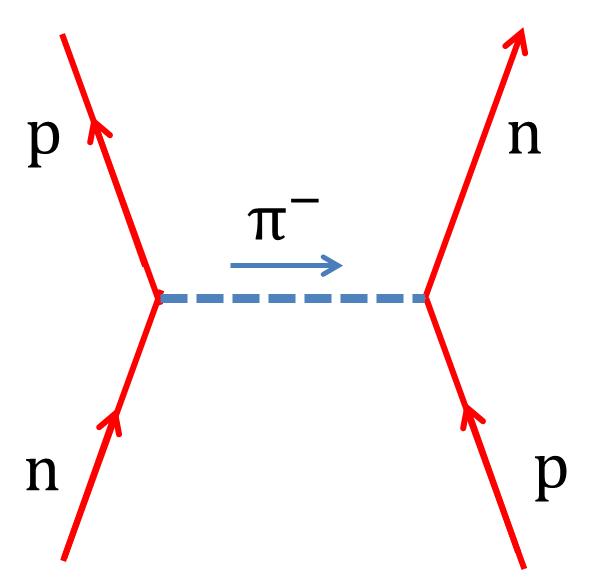
This should be compared to the mass of pions, with \(\pi^{+}\) being 140 MeV/c\(^2\) and \(\pi^{0}\) being 135 MeV/c\(^2\text{.}\) In the picture of Yukawa, the scattering of a proton and a neutron occurs with an exchange of a pion as illustrated by the Feynman diagram in Figure 58.2.3.
\begin{exercise} (a) Evaluate the electric and gravitational forces between two protons at a distance of 1 fm. (b) How many fold is the the electric force compared to the gravitational force? \end{exercise}
\begin{exercise} Consider a particle of mass $M= m_p/10$ and speed half of the speed of light $\frac{c}{2}$. What will be the de Broglie wavelength of the particle in fm? \end{exercise}
\begin{exercise} Pion was predicted to mediate the force between protons in the nucleus. Show that if we equate the de Broglie wavelength of the pion with speed close to the speed of light with the range of the nucleon-nucleon force we get the mass of the pion to be approximately the mass found experimentally. \end{exercise}
\begin{exercise} The energy-time uncertainty relation is given by \[ \Delta E \Delta t \geq \hbar/2. \] Here $\Delta E$ is the energy width of a decay process and $\Delta t$ is the time over which the decay takes place. Compute the minimum energy widths in MeV for the decay involving (a) an electromagnetic interaction, $\Delta t = 10^{-9}\:\textrm{s}$, (b) a weak interaction, $\Delta t = 10^{-20}\:\textrm{s}$, and (c) a strong interaction, $\Delta t = 10^{-23}\:\textrm{s}$. \end{exercise}
\begin{exercise} The energy-time uncertainty relation is given by \[ \Delta E \Delta t \geq \hbar/2. \] Here $\Delta E$ is the energy width of a decay process and $\Delta t$ is the time over which the decay takes place. A hydrogen atom makes a quantum transition from $n=3$ to $n=2$ with in a time $t=10^{-10}\:\textrm{s}$. (a) What is the energy of the photon that comes out? (b) What is the minimum width of the spectral line plotted versus energy rather than versus wavelength? (c) What is the the minimum width of the spectral line plotted versus wavelength? \end{exercise}