Circulation of Magnetic Field

Section 36.3 Circulation of Magnetic Field

Circulations of magnetic and electric fields play important role in understanding electric and magnetic phenomena fully. Circulation of a field combines the strength and direction properties of a field around a directed closed loop in space into one scalar quantity. If you have taken Calc III, you are already familiar with the concept of circulation of vector fields.

We calculate circulation of magnetic field \(\vec B\) around a closed path by summing the dot product \(\vec B\cdot \Delta\vec l\) for every piece \(\Delta l\) of the path, treated as length vector \(\Delta\vec l\) whose direction is the direction of traversal, and sum them all.

\begin{equation} \text{Circulation, } = \sum_\text{closed path} \vec B\cdot \Delta\vec l, \tag{36.11} \end{equation}

The length vector is same as the displacement vector on the loop. the loop usually is a closed path in space. It doesn’t have to have any physical object along the loop. On a straight segment of a directed loop, length vector will have one direction. When the loop turns a corner, the length vector must also turn the corner. If a loop is curved at some point, then the length vector at that point would be along the tangent to the loop.

Notice that the circulation depends on the direction you go around; if it is positive if go one way, then it will be negative if you go in the oposite direction. Circulation of a field also depends upon the path you choose for the circulation. I will illustrate this with the field of a current in an infinitely long wire.

Circulation in circle around a straight wire.

As an example, lets work out the circulation of magnetic field of current in a straight wire. As you know from a previous section, magnetic field of a long straight wire circulates around the wire in circles with the same magnitude \(B=\mu_0 I/ 2\pi r\) at all points of one circle of radius \(r\text{.}\) Let us denote this magnetic field by \(B(r)\text{.}\) The circulation of this magnetic field around a circle is easy to work out.

In this case, magnetic field \(\vec B\) and \(\Delta \vec l\) are both tangential and are in the same direction in every part of the circular path. Therefore, we get \(B(r)\Delta l\) from the dot product, and when we sum over all parts of the circle we get

\begin{equation*} \text{Circulation } = \sum_\text{circle} \vec B\cdot \Delta\vec l = B(r) \sum_\text{circle}\Delta l = B(r) \times 2\pi r. \end{equation*}

Circulation in another path near a straight wire.

Suppose we go one third way around the circle, then go parallel to the wire, and then go one third around the circle but in the opposite direction, and then finally go parallel o the wire returning to the original place. What will be the circulation?

You can show that the circulation will be zero. This happens because the contributions on path ab and cd cancel and the dot products on paths bc and da are zero since field and path are perpendicular to each other on segments of those paths.

\begin{align*} \amp \text{Circulation around abcda } \\ \amp \ \ = B(r) \dfrac{2\pi r}{3} + 0 - B(r) \dfrac{2\pi r}{3} + 0 = 0. \end{align*}

Circulation in multiples times around a straight wire.

What will happen if you go around a long straight wire multiple times so that the path is closed in the end?

The situation for three-times around is shown in Figure 36.37. You can see that in subsequent circles, the magnetic field and path are in opposite directions. Hence, circulation over two adjacent circles will be zero, and we will be left with circulation over one circle only.

\begin{equation*} \text{net circulation} = B(r) \times 2 \pi r. \end{equation*}

Subsection 36.3.1 (Calculus) General Definition of Circulation

The definition given in Eq. (36.11) with infinitesimal elements \(d\vec l\) of the loop makes the sum go over to a line integral over a closed path. We denote the resulting integral formally by symbol \(\oint\text{.}\) Therefore, circulation of field \(\vec B\) around a closed path \(C\) is defined by the following.

\begin{equation} \text{Circulation } = \oint_{C}\, \vec B \cdot d\vec l.\tag{36.12} \end{equation}

This is a conceptual integral. In a particular situation, you will need to convert this integral in variables that you can integrate over. Most closed paths we will encounter will be staraight or circular. In the case of stratight paths, we use Cartesian coordinates to write the path as

\begin{equation*} d\vec l = \hat u_x\, dx + \hat u_y\, dy + \hat u_z\, dz. \end{equation*}

In the case of circular path of radius \(R\text{,}\) with circle in the \(xy\) plane centered at origin, we use polar coordinates and write

\begin{equation*} d\vec l = \hat u_\phi\, R d\phi, \end{equation*}

where the unit vector \(\hat u_\phi\) depends on angle \(\phi\) and has the following expression in terms of Cartesian unit vectors.

\begin{equation*} \hat u_\phi = -\hat u_x\, \sin\,\phi + \hat u_y\, \cos\,\phi. \end{equation*}

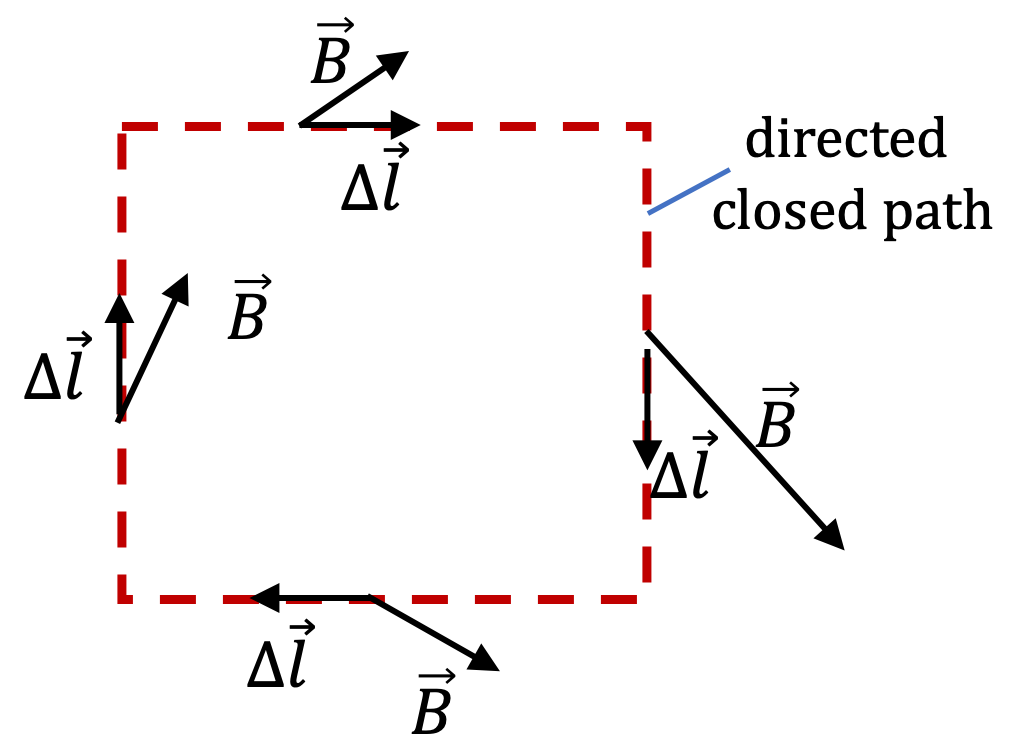
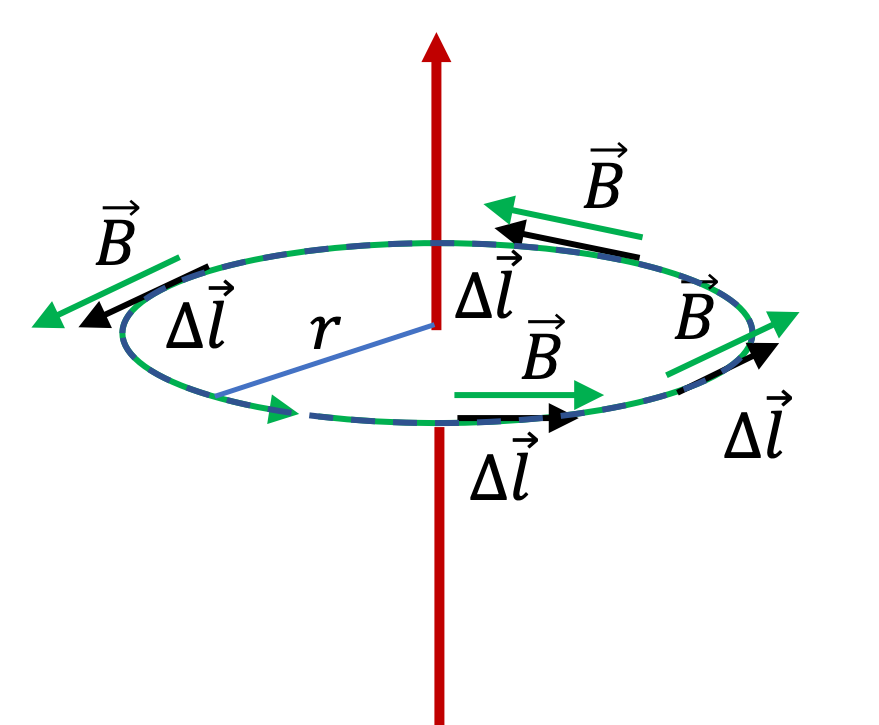
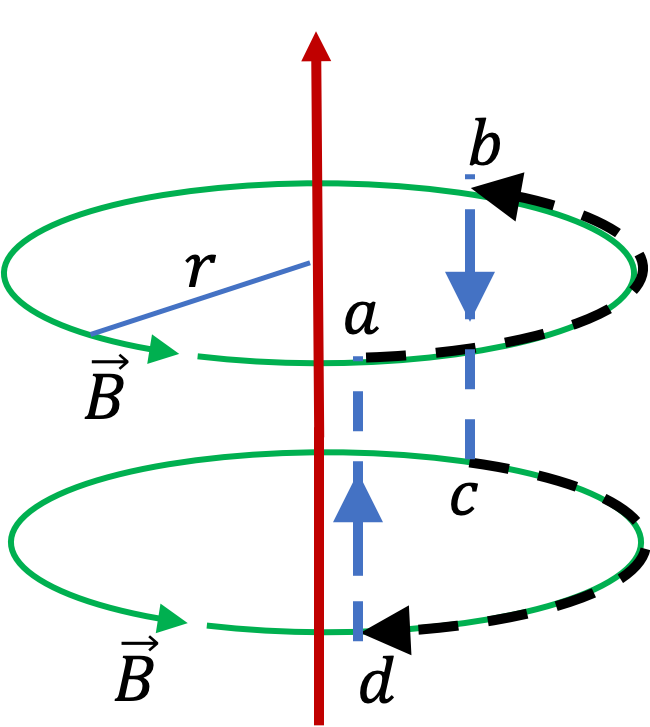
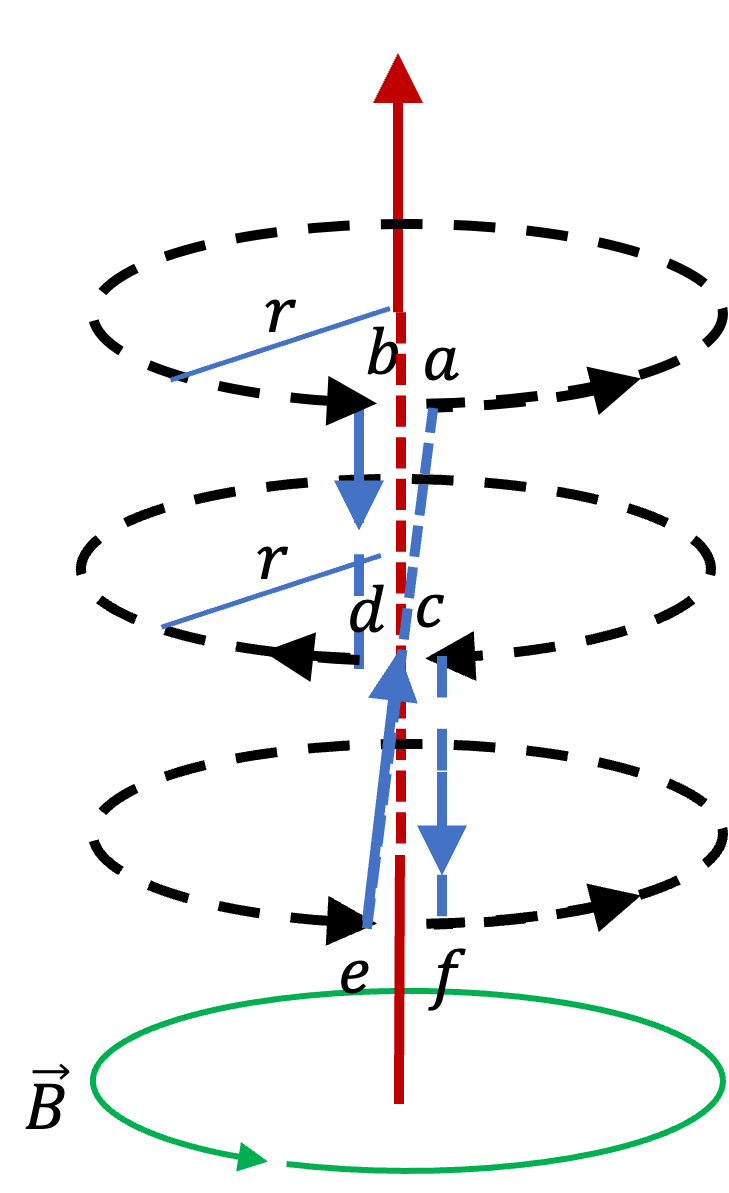
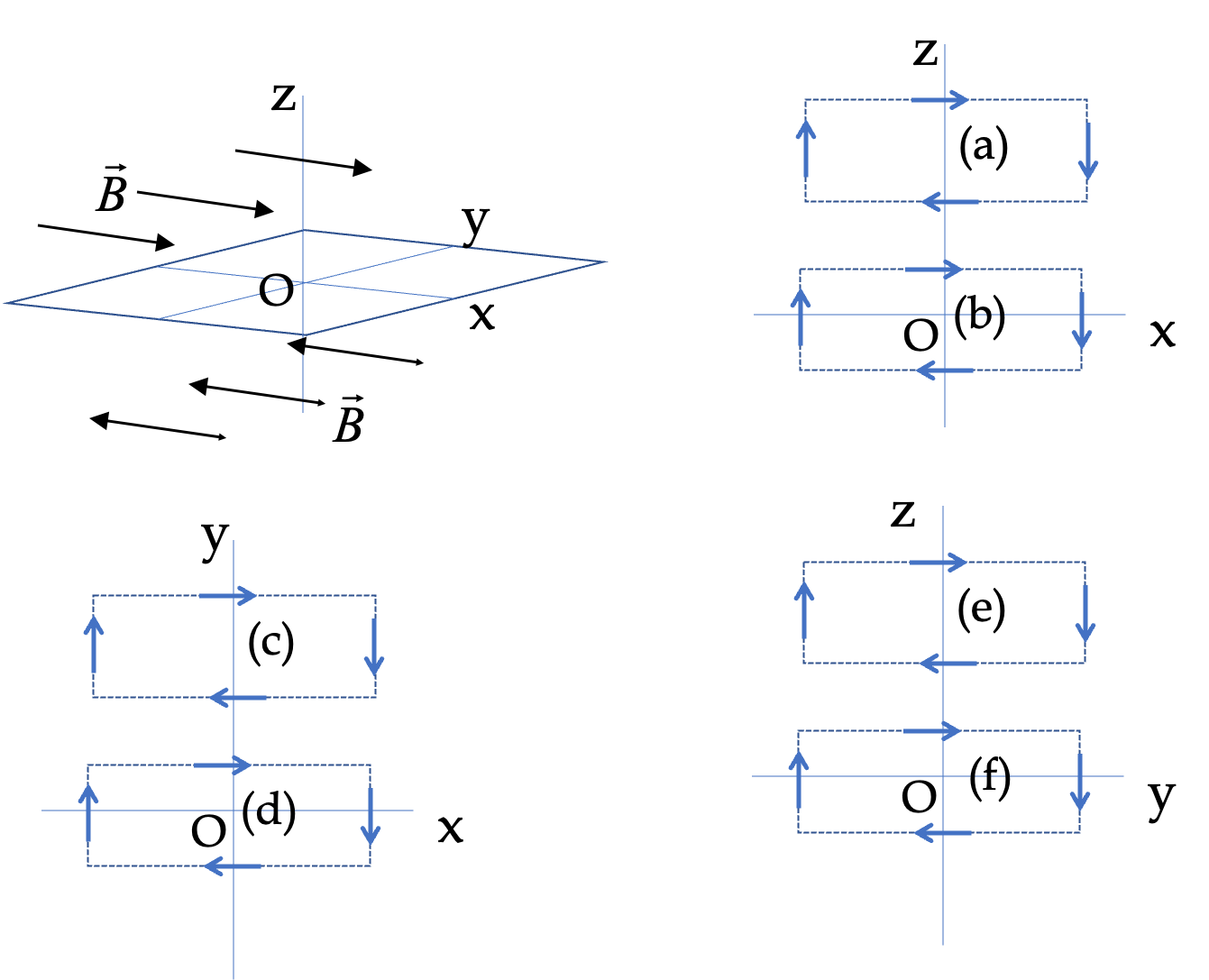
Example 36.38. Circulations Around Two Different Loops in Two-Region Uniform Magnetic Field.

Figure 36.39 shows two uniform magnetic field regions and a coordinate system with same magnitude, \(B_0\text{,}\) in the two regions, but oppositely directed. This would be magnetic field of a surface current in the \(xy\) plane flowing towards negative \(x\) axis. Above the \(xy\) plane field is directed towards positive \(y\) axis and below the plane, it is directed towards negative \(y\) axis.

Calculate the circulation of the magnetic field for the space loops (a) \(a-b-c-d-a\) and (b) \(e-f-g-h-e\) in the \(yz\)-plane shown in the figure.

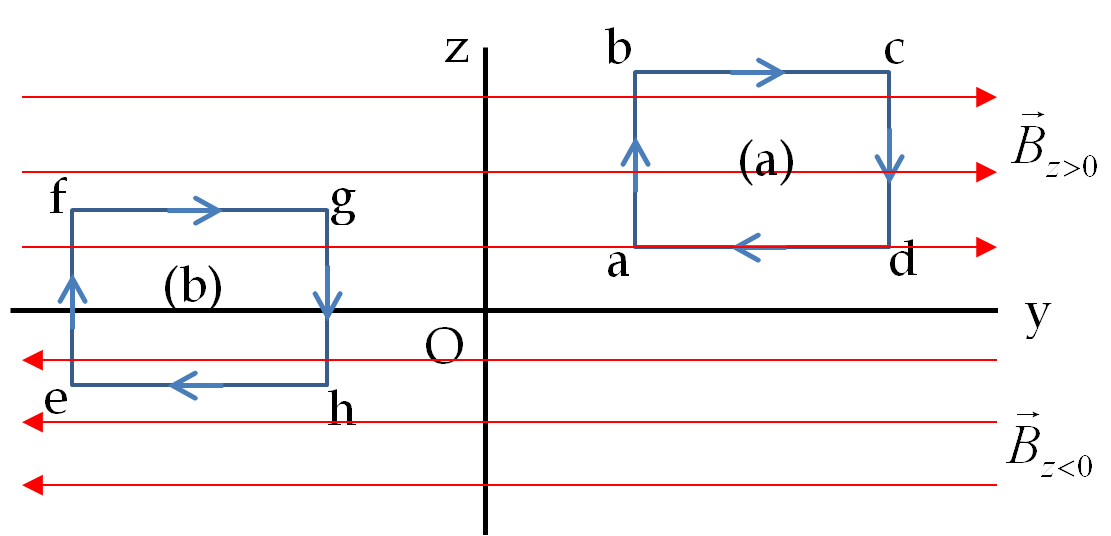
Answer.

(a) \(0\text{,}\) (b) \(2B_0l_\text{fg}\)

Solution 1. (a)

Here the loop \(\text{a-b-c-d-a}\) consists of four linear segments. We will compute \(\vec B\cdot \Delta \vec l\) on each and then sum them all. The calculation is relatively simple since \(\vec B\) is constant, and either parallel or perpendicular to the direction of each segment. The results are

\begin{align*} \amp \text{ab-segment: } \vec B\cdot \Delta \vec l = 0, \text{ (vectors pependicular), }\\ \amp \text{bc-segment: } \vec B\cdot \Delta \vec l = B_0 l_\text{bc}, \text{ (vectors same direction), } \\ \amp \text{cd-segment: } \vec B\cdot \Delta \vec l = 0, \text{ (vectors pependicular), }\\ \amp \text{da-segment: } \vec B\cdot \Delta \vec l = -B_0 l_\text{da}, \text{ (vectors opposite directions). } \end{align*}

Adding up the contributions the circulation around the loop is equal to zero.

\begin{equation*} \text{Circulation around a-b-c-d-a} = 0 + B_0 l_\text{bc}+0-B_0 l_\text{da} =0, \end{equation*}

since \(l_\text{bc} = l_\text{da}\text{.}\)

Solution 2. (b)

Here the loop \(\text{e-f-g-h-e}\) consists of four linear segments. We will compute \(\vec B\cdot \Delta \vec l\) on each and then sum them all. The calculation is relatively simple since \(\vec B\) is constant, and either parallel or perpendicular to the direction of each segment. The results are

\begin{align*} \amp \text{ef-segment: } \vec B\cdot \Delta \vec l = 0, \text{ (vectors pependicular), }\\ \amp \text{fg-segment: } \vec B\cdot \Delta \vec l = B_0 l_\text{fg}, \text{ (vectors same direction), } \\ \amp \text{gh-segment: } \vec B\cdot \Delta \vec l = 0, \text{ (vectors pependicular), }\\ \amp \text{he-segment: } \vec B\cdot \Delta \vec l = B_0 l_\text{he}, \text{ (vectors same directions). } \end{align*}

Adding up the contributions the circulation around the loop is

\begin{equation*} \text{Circulation around e-f-g-h-e} = 0 + B_0 l_\text{fg}+0+B_0 l_\text{he} = 2 B_0 l_\text{fg}, \end{equation*}

since \(l_\text{fg} = l_\text{he}\text{.}\)

Example 36.40. Circulation Around Two Circular Loops in an Inhomgeneous Magnetic Field.

Magnetic field lines in a region circulate in circles around a common center in counterclockwise direction with magnitude dpendeing upon the cylindrical radial coordinate \(s\) as follows.

\begin{equation*} B(s) = \dfrac{\alpha}{s}, \end{equation*}

where \(\alpha\) is some constant.

Find circulation of magnetic field around the loops indicated by dashed lines in the \(xy\) plane in figures (a) and (b)

Answer.

(a) \(2\pi\alpha\text{,}\) (b) \(0\text{.}\)

Solution 1. (a)

The loop is circular with direction counterclockwise, which is the same direction as the magnetic field. Therefore, on each segment of the loop,

\begin{equation*} \left.(\vec B \cdot d\vec l)\right|_{s=a} = \dfrac{\alpha}{a}\, \Delta l, \end{equation*}

Now summing these over the entire circle will just make \(\sum \Delta l = 2\pi a\text{,}\) the circumference. Therefore, the circulation around this loop will be

\begin{equation*} \text{Circulation } = \dfrac{\alpha}{a} \times 2\pi a = 2\pi\alpha. \end{equation*}

Solution 2. (b)

The full closed path is made up of four segments, two of which are straight segments and two others semi-circular. Therefore, the circulation is a sum of four sub-sums.

\begin{align*} \text{Circulation } \amp = \sum_\text{pqrsp}\vec B\cdot \Delta \vec l, \\ \amp = \sum_\text{pq}\vec B\cdot \Delta \vec l + \sum_\text{qr}\vec B\cdot \Delta \vec l + \sum_\text{rs}\vec B\cdot \Delta \vec l + \sum_\text{sp}\vec B\cdot \Delta \vec l \end{align*}

The individual pieces are easy to compute since \(\vec B\) is either perpnedicular to the path or has a constant magnitude and either parallel to the path or anti-parallel to path.

\begin{align*} \amp \sum_\text{pq}\vec B\cdot \Delta \vec l = \dfrac{\alpha}{a} \times \pi a = \pi\,\alpha, \\ \amp \sum_\text{qr}\vec B\cdot \Delta \vec l = 0,\\ \amp \sum_\text{rs}\vec B\cdot \Delta \vec l =-\dfrac{\alpha}{b} \times \pi b = -\pi\,\alpha, \\ \amp \sum_\text{sp}\vec B\cdot \Delta \vec l = 0. \end{align*}

Therefore, circulation around the closed path in question is

\begin{equation*} \text{Circulation } = \pi\,\alpha + 0 - \pi\,\alpha + 0 = 0. \end{equation*}

Exercises 36.3.2 Exercises

1. Calculating Circulation of Magnetic Field on Various Loops Ex1.

A magnetic field is uniform with magnitude \(B_0\) above \(z=0\) plane and points towards the positive \(x\)-axis and uniform with with same magnitude \(B_0\) below \(z=0\) axis but points towards the negative \(x\)-axis as shown in Figure 36.41. Find the circulation of the magnetic field for the closed loops (a)-(f). Note the loops have been drawn in different planes.

Solution 1. a

The circulation around this loop will be zero since the contribution of the bottom part of the loop is negative and cancels the contribution from the top. The contributions of the sides are zero since \(\vec B\) is perpendicular to the line elements.

Solution 2. b

Let the path have length \(l_x\) parallel to the \(x\)-axis. The line integral \(\oint\: \vec B\cdot d\vec l\) has zero value on the sides since \(vec B\) is perpendicular to the line elements, positive values for both the top part and the bottom part since in each part the line directed elements have the same direction as the direction of the field. Hence, circulation will be equal to \(2 B_0 l_x\text{.}\)

Solution 3. c,d,e,f

(c), (d), (e), and (f) will all give zero circulation.

2. Calculating Circulation of Magnetic Field on Various Loops Ex2.

A non-uniform magnetic field exists in a region of space such that the magnitude of the field varies with distance \(r\) from the \(z\)-axis as

\begin{equation*} B = \frac{\alpha}{r}, \end{equation*}

where \(\alpha\) is a constant, and the direction of the field in the \(xy\)-plane as shown in figure below. Find the circulation of the magnetic field for the closed loops (a)-(c). Loop (b) is a three-dimensional loop in the shape of a helix which has a circular projection of radius \(r\) on the \(xy\)-plane as indicated in the figure.

Solution 1. a

The loop for the circulation coincides with one of the loops of the magnetic field lines where the magnetic field has a constant magnitude \(\alpha/r\text{.}\) Since magnitude \(B\) is constant and line elements are in the same direction as \(\vec B\text{,}\) the circulation will be equal to the product of the \(B\) and the length of the loop, which is \(2\pi r\text{.}\) Therefore, the circulation will be \(2\pi\alpha\text{.}\)

Solution 2. b

It is difficult to compute the line integral directly here. But we can use Ampere’s law to deduce that the circulation around this loop will be equal to the circulation around the loop in (a) since they enclose same current. Hence, circulation = \(2\pi\alpha\text{.}\)

Solution 3. c

Same reason as in (b). Circulation = \(2\pi\alpha\text{.}\)

3. Calculating Circulation of Magnetic Field on Various Loops Ex3.

A magnetic field exists in a region of space such that the magnitude of the field varies with distance \(r\) from the \(z\)-axis as

\begin{equation*} B = \begin{cases} B_0 \amp r\lt R\\ 0 \amp r\gt R \end{cases} \end{equation*}

where \(B_0\) is a constant, and the direction of the non-zero field is towards the positive \(z\)-axis as shown in the figure below. Find the circulation of the magnetic field for the closed loops (a)-(e). Note the loops have been drawn in different planes.

Solution 1. a

Since \(vec B\) is perpendicular to the line elements of the loop, the circulation will be zero dur to \(\vec B\cdot d\vec l = 0\) on each line element \(d\vec l\text{.}\)

Solution 2. b

Same as (a).

Solution 3. c

Here the two line segments parallel to the \(z\)-axis will give non-zero contributions to the line integral \(\oint\vec B\cdot d\vec l\text{,}\) but their signs will be opposite since while on the left side \(\vec B \parallel d\vec l\text{,}\) on the right side they are antiparallel. The circulation around the entire loop will equal zero.

Solution 4. d

Circulation will be zero. [Can you see why? Think doing the line integral on each segment.]

Solution 5. e

The only non-zero contribution will come from the path at \(x=0\text{.}\) Let \(l_z\) be the length of the path on at \(x=0\text{.}\) We will get circulation = \(B_0\:l_z\text{.}\)

Prev Top Next