Section 12.5 Angular Momentum Conservation and Kepler’s Second Law
Kepler’s second law is a consequence of the conservation of angular momentum. We look at the motion of one planet and the Sun, a two-body problem interacting with gravitational form. We will work in the CM frame, where the problem simplifies to the motion of one particle of mass equal to reduced mass.
\begin{equation}
\mu\dfrac{d^2\vec r}{dt^2} = -G_N \dfrac{\mu\, M}{r^2}\, \hat u,\tag{12.27}
\end{equation}
where \(\hat u\) is unit vector pointed towards the origin, the radially inward direction. We can rewrite this as
\begin{equation}
\dfrac{d(\mu \vec v)}{dt} = -G_N \dfrac{\mu\, M}{r^2}\, \hat u,\tag{12.28}
\end{equation}
where \(\vec v = d\vec r/ dt \text{.}\) The left side is the rate of change of momentum. Taking cross product with \(\vec r\) on both sides we get
\begin{equation}
\vec r \times \dfrac{d(\mu \vec v)}{dt} = -G_N \dfrac{\mu\, M}{r^2}\, \vec r \times \hat u.\tag{12.29}
\end{equation}
The right side is zero since there is \(180^\circ \) angle between \(\vec r\) and \(\hat u\text{.}\) By moving \(\vec r \times \) inside the \(d/dt\) on the left side, we can show that
\begin{align*}
\dfrac{d( \vec r \times \mu \vec v)}{dt} \amp =\dfrac{d\vec r}{dt} \times \mu \vec v + \vec r \times \dfrac{d(\mu \vec v)}{dt},\\
\amp = \vec v \times \mu \vec v + \vec r \times \dfrac{d(\mu \vec v)}{dt}\\
\amp = 0 + \vec r \times \dfrac{d(\mu \vec v)}{dt}
\end{align*}
Therefore, Eq. (12.29) gives the following equation.
\begin{equation}
\dfrac{d (\vec r \times \mu \vec v)}{dt} = 0.\tag{12.30}
\end{equation}
Since \(\vec r \times \mu \vec v\) is angular momentum of the relative motion, this is the statement of conservation of angular momentum. We can pull \(\mu\) out, giving us the following equation obeyed by the trajectory \(\vec r(t) \text{.}\)
\begin{equation}
\vec r \times \vec v = \vec c,\tag{12.31}
\end{equation}
where \(\vec c\) is a constant vector. Rewrite this as
\begin{equation}
\vec r \times d\vec r = \vec c\, dt,\tag{12.32}
\end{equation}
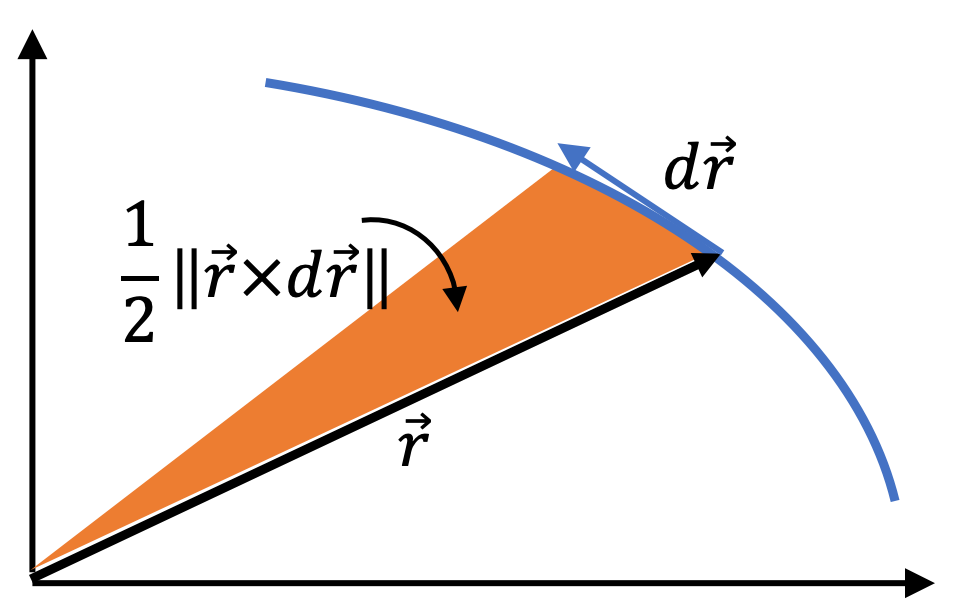
and note that the magnitude of \(\vec r \times d\vec r\) is the area of the rectangle formed by vectors \(\vec r \) and \(d \vec r\text{,}\) which is twice the area swept by vector \(\vec r \text{.}\)
\begin{equation}
\vec r \times d\vec r = 2\times \text{Area swept by }\vec r.\tag{12.33}
\end{equation}
\begin{equation*}
\int_{\vec r(t_i)}^{\vec r(f)} \vec r \times d\vec r = \vec c (t_f - t_i),
\end{equation*}
where the left side is twice the area swept by vector \(\vec r\) as shown in Figure 12.30. Writing the magnitudes only with \(\Delta A\) for area swept and \(\Delta t\) for time interval, we will get
\begin{equation*}
\dfrac{\Delta A}{\Delta t} = c/2,\text{ a constant.}
\end{equation*}
That is, the radial position vector of \(\mu\) sweeps out equal area in equal time. Since mass of Sun is much greater than most planets, particle \(\mu\) can be replaced by the planet alone, which is the observation made by Kepler in his second law of planetary motion.
By Newton’s analysis, we get more than Kepler’s law - we see the precise variables we should look at when we are computing the area swept. Additionally, we see that Kepler’s second law is a consequence of conservation of angular momentum. We will also see that Kepler’s third law has an error that Newton’s analysis corrects.

