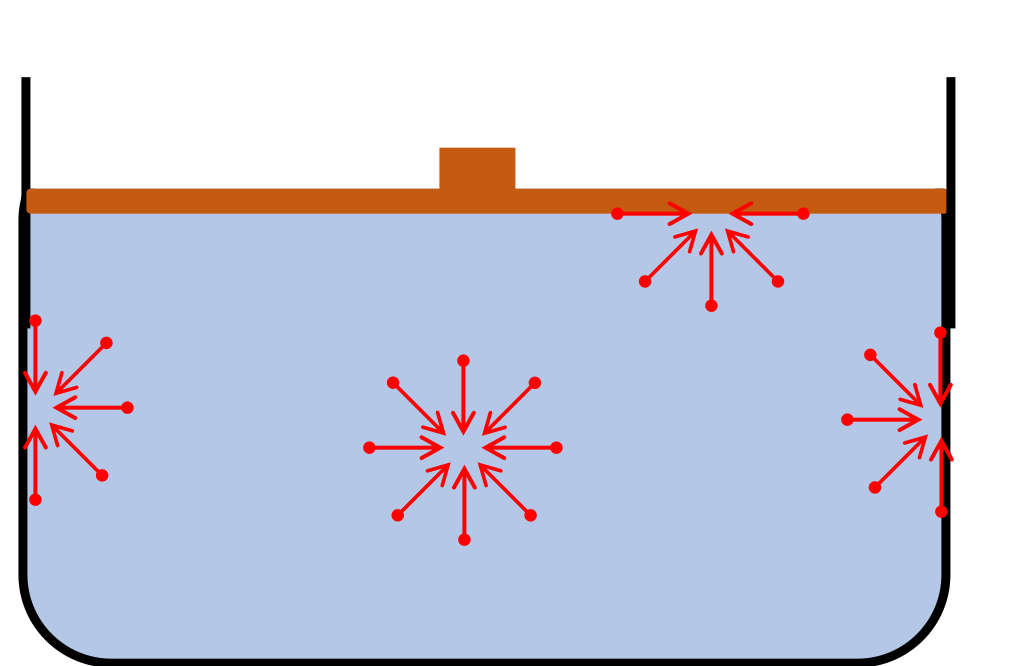
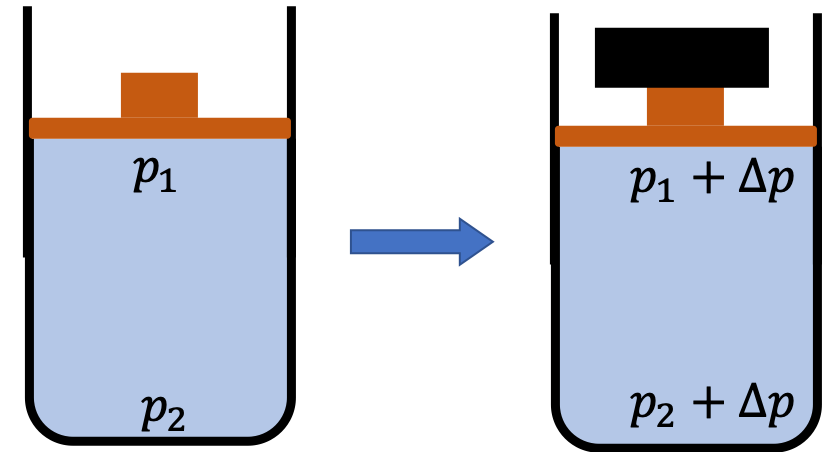
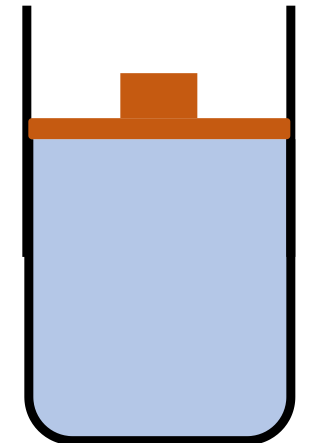
Example 17.25. Pressure Changes from Weight of a Block Placed on Piston.
A freely movable piston of mass 100 kg covers water in a rigid cylinder of radius 5 cm touching the surface of the water.
(a) What is the pressure at a depth of 50 cm from the top of water?
(b) A block of steel of mass 300 kg is placed on the piston. What is the new pressure at a depth of 50 cm from the top?
Answer.
(a) \(2.31\times 10^5\text{ Pa}\) , (b) \(6.05\times 10^5\text{ Pa}\text{.}\)
Solution 1. (a)
(a) The pressure at \(50\text{ cm}\) depth will be the sum of atmospheric pressure, the pressure due to the weight of the piston, and the \(50\text{-cm}\) column of water above the point where we want the pressure. We need area of cross-section.
\begin{equation*}
A = \pi R^2 = \pi \times 0.05^2 = 0.007854\text{ m}^2.
\end{equation*}
Therefore,
\begin{align*}
p \amp = p_0 + \dfrac{mg}{A} + \rho g h, \\
\amp = 1.013\times 10^{5} + \dfrac{100\times 9.81}{0.007854} + 1000\times 9.81\times 0.50,\\
\amp = 2.31\times 10^5\text{ Pa}.
\end{align*}
Solution 2. (b)
(b) According to Pascal’s second principle, the new pressure will be the old pressure plus the additional pressure from new weight.
\begin{equation*}
2.31\times 10^5 + \dfrac{300\times 9.81}{0.007854} = 6.05\times 10^5\text{ Pa}.
\end{equation*}