Image Formation by Reflection

Section 44.1 Image Formation by Reflection

When you look into a plane mirror, you see your image behind the mirror. However, image does not have to always form behind a mirror. For instance, you are far enough from a concave-shaped mirror, the image will form in front of the morror. In this section we will study how rays of light emanating from an object can form these images upon reflection.

By the term object, we mean a source of light. Now, this source could be a primary source of light such as the Sun or a light bulb. But, the light may also be a a re-emitted light from an illuminated object, such as a person or a book.

When the rays of light from a single point of the object interact with an optical device, such as a mirror or lens, new rays emerge from the optical device due to reflection and refraction effects as we have seen in the last chapter. These new rays whose origin is same point of the object will either converge to a point in space or appear to diverge away from a point in space. This point in space is the image point of the point on the object.

The image is said to be a real image if the rays emerging from the optical device converge on a point in space. But, if they appear to be diverging away from a point in space then the image is called a virtual image.

Figure 44.1. In this picture sunlight is the primary source of light. The vase is the object, from which diffuse reflection provide secondary light that reflect off of the mirror and form a virtual image behind the plane mirror. source: https://en.wikipedia.org/wiki/Mirror_image#/media/File:Mirror.jpg

Subsection 44.1.1 Image in a Plane Mirror

How does an image form behind a plane mirror? For simplicity, we will examine image of a point object, which can be very small source of light. This is shown as point P in Figure 44.2. We wish to find the location of the image of this point object by examining the reflected rays.

Figure 44.2. Incident rays 1 and 2 from object P are chosen arbitrarily and when they strike the reflecting surface the direction of the reflected rays 1’ and 2’ are obtained using the law of reflection. All reflected rays, when extended backwards, meet at a single point behind the mirror at the virtual image point Q.

Note that infinitely many rays emanate from a point source. To find the image of point P we need to follow the paths of only two of these rays, shown in Figure 44.2 as P-A-P and P-B-C, which are labelled as \(\text{1-1}^{\prime}\) and \(\text{2-2}^{\prime}\text{.}\) We find that the reflected rays \(\text{1}^{\prime}\) and \(\text{2}^{\prime}\) are diverging away from each other. To find the image behind the mirror, we extend these reflected rays backwards. Of course there are no real rays behind the mirror. That is why these extensions are called virtual rays. The backward extensions of the real rays meet at the point Q.

Now, if you took any other ray from P and performed the reflection and then backward extension of the reflected ray, you will find that all the extensions meet at the same point Q as shown in Figure 44.3. Point Q is the image of point P. The image is virtual since only virtual rays meet at the image. We say that plane mirror forms virtual image.

Figure 44.3. All reflected rays from point object P appear to come from the virtual image point Q.

An extended object such as a cup is treated as a collection of points, and its image is found from the image of each of its points. The image of an extended object is then made from the collection of the image points. A simple object OP shown in Figure 44.4 has two end points. Therefore, you will need to draw four incident rays, two from P and two from O to find the image IQ. The size of the image IQ is equal to the size of the object OP in this case.

Figure 44.4. Image formation of an extended object PQ modeled by its two end points P and Q.

In a three-dimensional situation in Figure 44.5 we see that right side of the vase has the image at the left side of the image of the vase and the left side of the vase at the right side of the image. This makes the image reflected to have left-side switched, but the top and bottom do not get switched.

Figure 44.5. Image formation of a three-dimensional extended object. Note the left-right switch between object and image, but not top-bottom switch.

Subsection 44.1.2 Multiple Images

If an object is in front of two mirrors, you get images in both mirrors. So, you would think that you wll get two images, one in each mirror. But, that is not so. You can get multiple images, depending on how the two mirrors are oriented. This happens because, an image behind one mirror serves as a brand new object for the other mirror and you get an image of image.

In Figure 44.6, where mirrors are at right angle to each other, you get three images as shown by the drawing of rays. Image \(\text{Q}_1\) and \(\text{Q}_2\) result from rays that reflect off only one of the mirrors M1 or M2. But \(\text{Q}_{12}\) which is the same as the image of \(\text{Q}_1\) in M2 or the image of \(\text{Q}_2\) in M1 is formed by rays that reflect off both mirrors. To find the image \(\text{Q}_{12}\) you have to look behind the corner of the two mirrors as shown in Figure 44.7.

Figure 44.6. Formation of three images from two mirrors at right angle to each other.

Figure 44.7. Three images of a pin from two mirrors at right angle to each other.

If two mirrors are inclined by \(60^\circ\) you will get five images! If you have two mirrors facing each other in a parallel way, you can get infintely many images if you place an object at the midway between them.

Exercises 44.1.3 Exercises

1. Images by Two Mirrors with an Acute Angle Between Them.

Two mirrors are inclined at an angle of \(60^{\circ}\) and an object is placed at a point that is equidistant from the two mirrors. Use a protractor to draw rays accurately and locate all images. You may have to draw several figures so that that rays for different images do not clutter your drawing.

Hint.

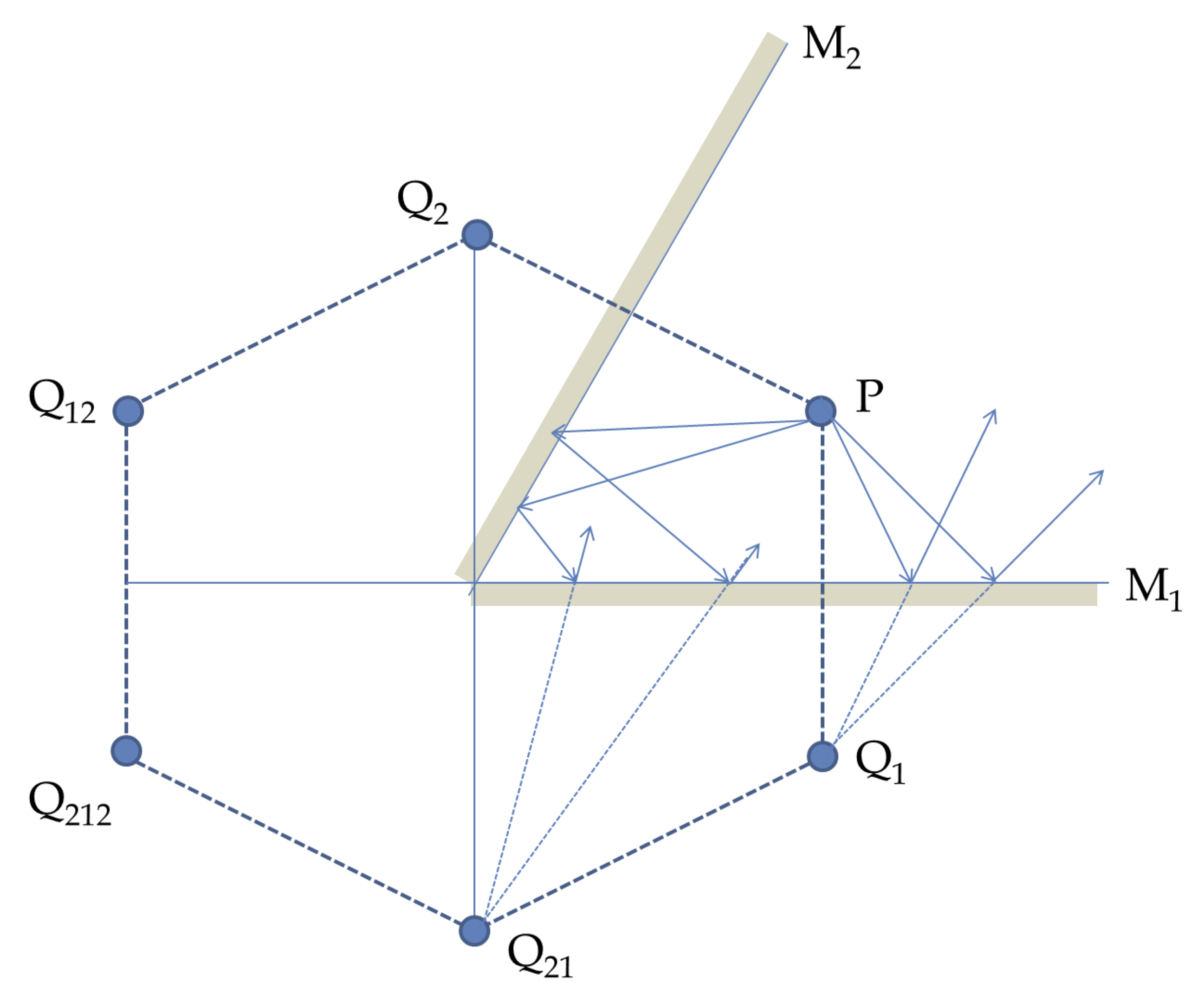
Draw rays to locate five images. They will be at the corners of a regular hexagon.

Answer.

See the solution.

Solution.

We can think of each mirror being infinitely long and look for image of image from one mirror into the other. Since angle is \(60^{\circ}\text{,}\) they start to overlap and end with only five images as shown in Figure 44.8.

The images are labeled with subscript that indicate the reflections from the two mirrors. The rays leading to two of the images are shown in the figure and the student is encouraged to work out representative rays that lead to other images.

Figure 44.8. Figure for Exercise 44.1.3.1.

2. Images of an Object Placed Between Two Parallel Mirrors Facing Each Other.

Two parallel mirrors are facing each other and are separated by a distance of \(b=3.0\text{ cm}\text{.}\) A point object is placed \(a= 1.0\text{ cm}\) from one of the mirrors. Find the coordinates of all the images.

Hint.

There will be two series of images and images of images. Start with an image reflected in one of the mirrors, and find all the images of images of this image. Do the same strating with the first image in the other mirror.

Answer.

With origin at left mirror, \(x_0=a\text{,}\) we get images are the following x-coordinates, where \(n=1, 2, 3, \cdots\text{,}\) \(x_{2n-1} = -x_{2(n-1)}\text{,}\) \(x_{2n} = 2b-x_{2n-1}\text{,}\) \(x^\prime_{2n-1} = 2b-x_{2(n-1)}\text{,}\) \(x^\prime_{2n} = - x^\prime_{2n-1}\text{.}\)

Solution.

Note that image in one mirror will reflect in the other mirror and form an image of image in that mirror. That image, in turn, will reflect in the first mirror and we will get its image. Thus, we will get a series of images.

To find the location of all images we start with the first image in one of the mirrors, say the left mirror and then find the image of this image on the right mirror, and so on as shown in Figure 44.9 below. We will repeat this work similarly for the first image in the right mirror.

Let \(x=0\) be the location of the left mirror, \(x=a\) the location of the object and \(x=b\) the location of the right mirror. Then, \(x\) coordinates of the images in this figure will be

\begin{align*} \amp x_1=-a,\\ \amp x_2=2b-x_1,\\ \amp x_3=-x_2,\\ \amp x_4=2b-x_3,\ \text{etc.} \end{align*}

We can write these in a more conpact notation for even and odd numbered images by introducing \(x_0=a\text{.}\) For \(n = 1,\, 2,\, 3,\, \cdots\text{,}\) we have images at

\begin{align*} \amp x_{2n-1} = -x_{2(n-1)}, \\ \amp x_{2n} = 2b-x_{2n-1}. \end{align*}

Figure 44.9. Figure for Exercise 44.1.3.2 when first reflected in the left mirror. Here O is the origin of the \(x\) coordinate system.

Using Figure 44.10 When we start with the first image in the right mirror the images are located as follows.

\begin{align*} \amp x^\prime_1=2b-a,\\ \amp x^\prime_2= - x^\prime_1,\\ \amp x^\prime_3=2b - x^\prime_2,\\ \amp x^\prime_4 = -x^\prime_3 ,\ \text{etc.} \end{align*}

We can write these in a more conpact notation for even and odd numbered images by introducing \(x_0\) for \(a\text{.}\) For \(n= 1, 2, 3, \cdots\text{,}\) we have images at

\begin{align*} \amp x^\prime_{2n-1} = 2b-x_{2(n-1)}, \\ \amp x^\prime_{2n} = - x^\prime_{2n-1}. \end{align*}

Figure 44.10. Figure for Exercise 44.1.3.2 when first reflected in the right mirror. Here O is the origin of the \(x\) coordinate system.

Prev Top Next