Section 46.6 Birefrengence
In an isotropic material such as water and glass, the refractive index is same in all directions in the material. But when you have a crystalline material, it may have different refractive indices in different directions. Uniaxial crystals such as calcite (Calcium carbonate), tourmaline (Boron silicate) and quartz (Silicon oxide) have a special direction called the optic axis. These crystals are examples of birefringent crystals.
In birefringent crystals, refractive index of light is different depending on the polarization of the wave relative to the optic axis. When an electromagnetic wave is incident along the optic axis, only one wave comes out of the crystal, but when light is incident at an angle to the optic axis, two waves come out as illustrated in Figure 46.24.
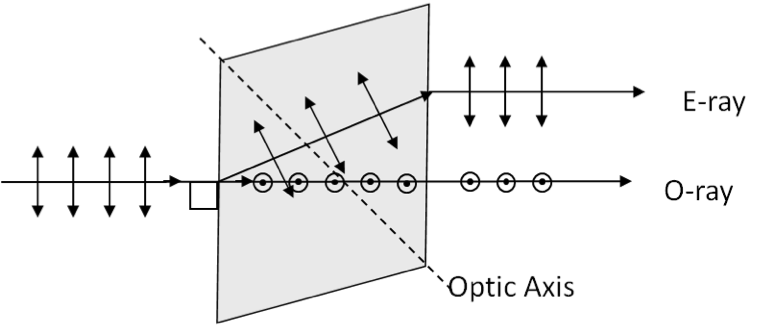
Clearly, one of these directions is consistent with Snell’s law of refraction, and the other is not. The wave in the crystal that obeys Snell’s law is called the ordinary or O-ray, and the strangely behaving ray is called the extraordinary or E-ray. Due to the generation of two rays, the O-ray and the E-ray, you see two images when you look through a birefringent crystal as illustrated in Figure 46.25.

The refractive index of the ordinary ray \(n_o\) may be larger or smaller than the refractive index of the extraordinary ray \(n_e\text{.}\) The difference \(n_e - n_o\) is called the birefringence of the birefringent crystal. The values of some commonly used birefringent crystals are given in Table 46.26.
| Crystal | \(n_o\) | \(n_e\) | \(n_e - n_o\) |
| Calcite | \(1.6585\) | \(1.4864\) | -0.1721 |
| Quartz | \(1.5443\) | \(1.5534\) | 0.0091 |
| Sodium Nitrate | \(1.5854\) | \(1.3369\) | -0.2485 |
| Tourmaline | \(1.669\) | \(1.638\) | -0.031 |
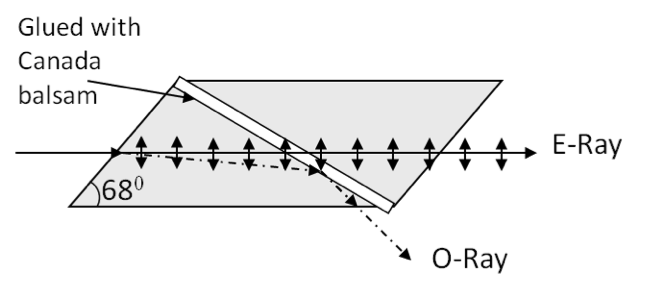
Polarizers can be constructed by using birefringence. One such birefringent polarizer is a Nicol prism shown in Figure 46.27. The Nicol prism is made by cementing two prisms of calcite with Canada balsam which is transparent in the visible spectrum and has a refractive index between the ordinary and extraordinary rays. The cemented surface is oriented such that the ordinary ray suffers a total internal reflection at the prism/balsam interface. That leaves the extraordinary ray enter the second prism and emerge from the second prism.