Section 48.2 The Huygens-Fresnel Principle
Fresnel made use of highly successful model of wave propagation put forth by Christiaan Huygens in 1690. This model is called Huygens’ principle. Huygen imagined that each point of a wavefront serves as a source of new waves, which he called secondary wavelets. These wavelets have the same frequency and speed as the original wave and are spherical waves. The envelop of these secondary wavelets make up the wavefront at a later time. Figure 48.3 illustrates Huygens’ principle by evolution of a primary wavefront, or simply a wavefront.
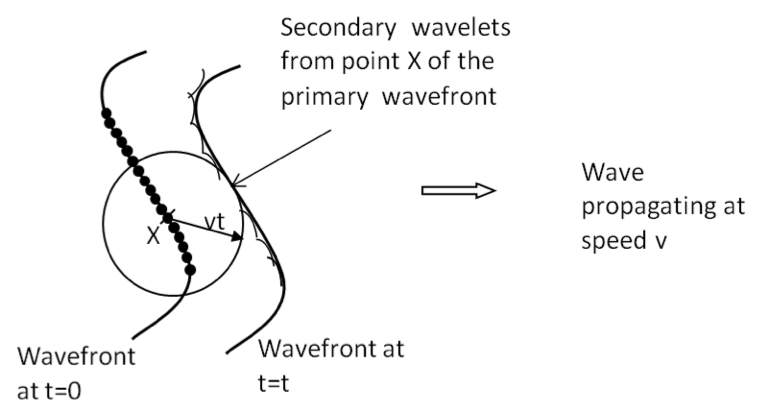
Huygens’ principle suffers from several drawbacks. It does not tell us what to do with the backward traveling part of the secondary spherical wavelet. Furthermore, it makes use of only the envelop of the secondary wavelets, and does not tell us what to do with the rest of the wavelet. Most problematic part was that it gave rise to the same wavefront regardless of the value of the wavelength. This contradicted observation that diffraction patterns in the same setup depended on the wavelength.
Augustin Jean Fresnel used the ideas of interference to modify Huygens’ principle so that one can understand the diffraction phenomena better. Fresnel hypothesized that every point of a primary wave could be thought of as producing secondary wavelet. But rather than their envelop, it was their overlap and interference that formed the primary wavefront later. The modified version is called the Huygens-Fresnel principle.
In the subsequent sections, we will now apply the Huygens-Fresnel principle to simple cases of diffraction from single-slit, double-slit, circular aperture, and diffraction grating to gain qualitative and quantitative understanding of the diffraction phenomena. It turns out that near an aperture or an obstacle, the pattern is very complicated, but the pattern simplifies when observed far away. We will study only this far-away cases in this book. This far away case, also called the far field case, is called Fraunhofer diffraction and the complicated nearby or near field case is called Fresnel diffraction.

