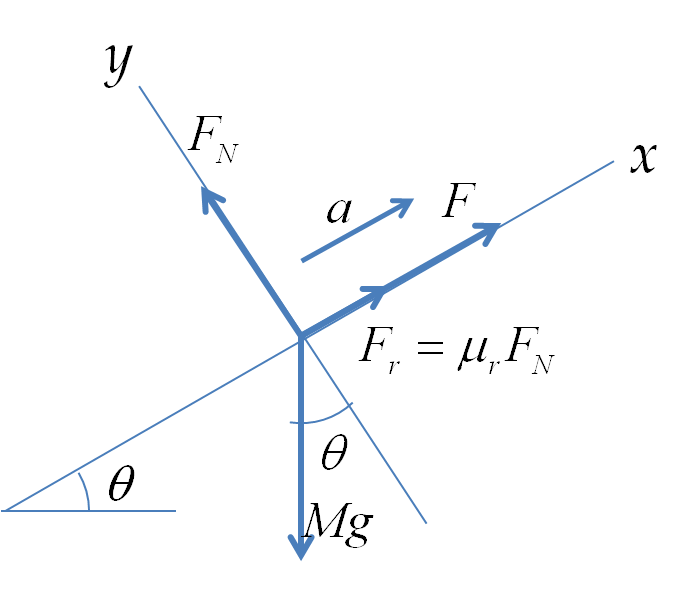
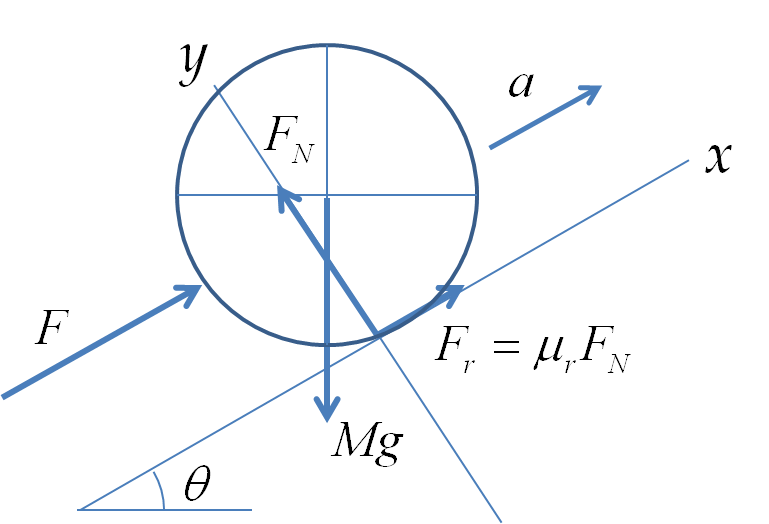
Example 9.128. Speed of a Ball Rolling Down an Incline.
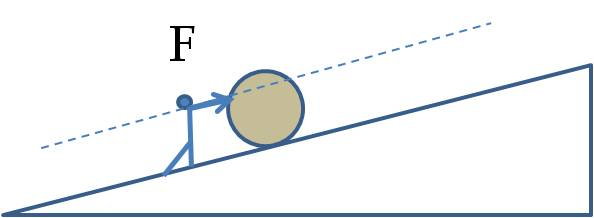
A spherical marble of radius \(R\) rolls down in a straight line on an inclined plane with the angle of inclination \(\theta\) without slipping. What will be the speed of the marble when it has rolled down a distance \(D\) on the incline?

Answer.
\(\sqrt{\dfrac{10}{7}\,g\,D\,\sin\,\theta}\text{.}\)
Solution.
The energy conservation can be used to state that the loss of gravitational potential energy will equal the total kinetic energy. Let \(M\) be the mass f the marble.
\begin{equation*}
\dfrac{1}{2} M V_\text{cm}^2 + \dfrac{1}{2}I\omega^2 = M g h,
\end{equation*}
where
\begin{equation*}
\omega = \dfrac{V_\text{cm}}{R},\ \ I = \dfrac{2}{5}MR^2,\ \ h = D\,\sin\,\theta.
\end{equation*}
Therefore
\begin{equation*}
\dfrac{7}{10}M V_\text{cm}^2 = M g D\sin\,\theta,
\end{equation*}
from which mass cancels out, and we get
\begin{equation*}
V_\text{cm} = \sqrt{\dfrac{10}{7}\,g\,D\,\sin\,\theta}.
\end{equation*}