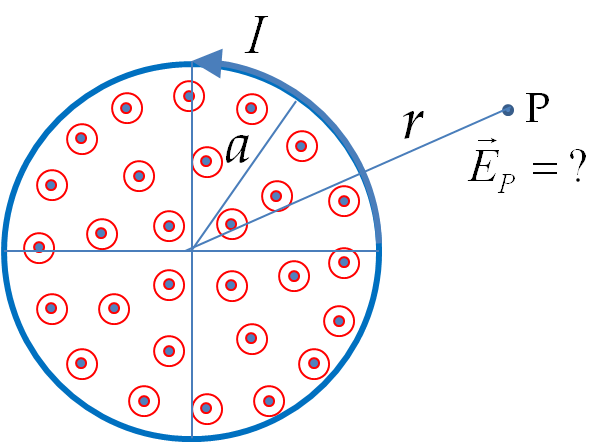
Example 38.41. (Calculus) Electric Field from a Varying Magnetic Field.
A long cylindrical solenoid of radius \(a\) having \(n\) turns per unit length carries a time-dependent current \(I(t)\text{.}\) Find electric field at a point P outside the solenoid as shown in figure, where, for the sake of clarity, only a cross-section of the solenoid is shown.
Solution.
Recall that the current in a solenoid produces a uniform magnetic field inside the solenoid of the magnitude \(\mu_0 n I\) and zero outside the solenoid. The direction of the magnetic field depends on the current direction given by the right-hand rule of Biot-Savart’s law: if you look down the axis, then the direction of magnetic field will be towards you if the current loops around in a counter-clockwise direction as given in the problem statement.
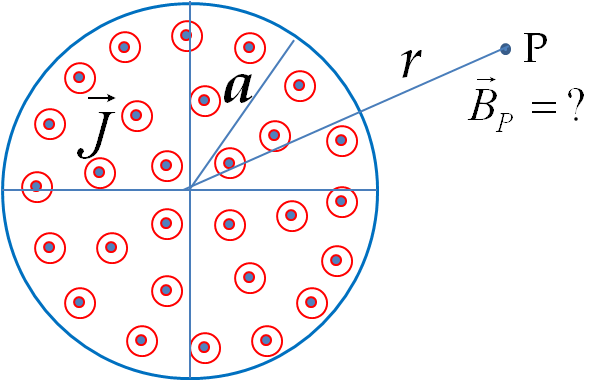
From the analogy of Ampere’s law and Faraday’s law discussed above, we note that the problem here is analogous to the Ampere’s law problem of finding magnetic field outside a straight wire that carries a uniform volume current density \(\vec J\) as shown in the figure.
Therefore, in the present situation we can claim that the electric field will circulate in circles around the magnetic field just as the magnetic field of a straight wire circulates around the current. Following the Ampere’s law procedure for a straight wire, we choose an “Amperian loop” in the shape of a circle that passes through the field point P as shown in Figure 38.43. Now, we equate the circulation of electric field around the Amperian loop with the “enclosed” rate of change of magnetic flux through the Amperian loop.
\begin{equation*}
\text{Circulation of }\vec E = - \text{ Enclosed rate of change of magnetic flux.}
\end{equation*}
Since the electric field has the same amplitude at all points of the circle the circulation is just a product of the amplitude of the electric field and circumference of the circle of radius \(r\text{,}\) which is the distance of field point P from the axis of solenoid. The enclosed magnetic flux is also easy to calculate here since the magnetic field is zero outside the solenoid.
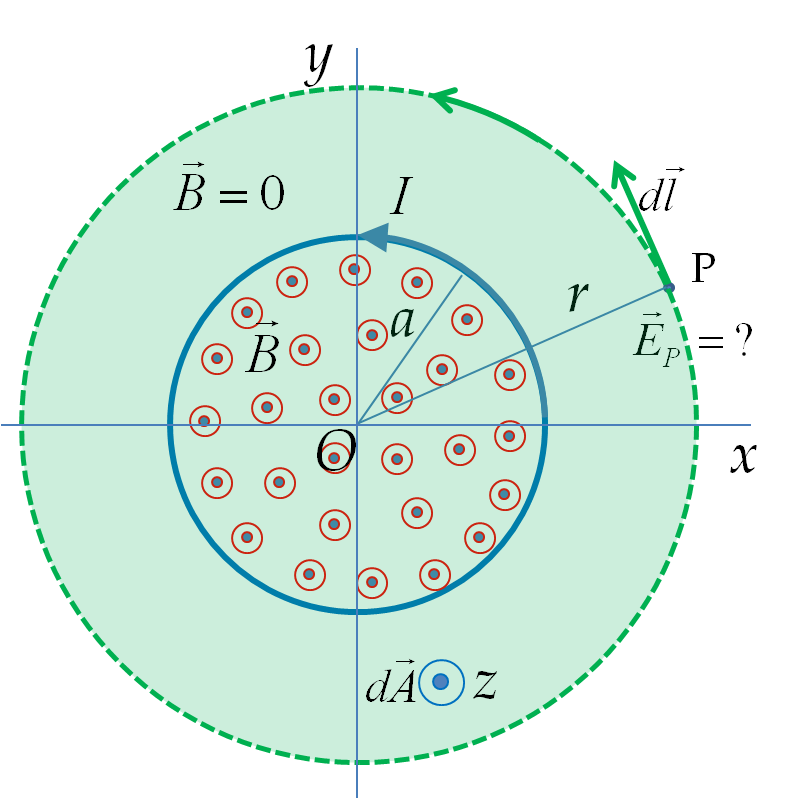
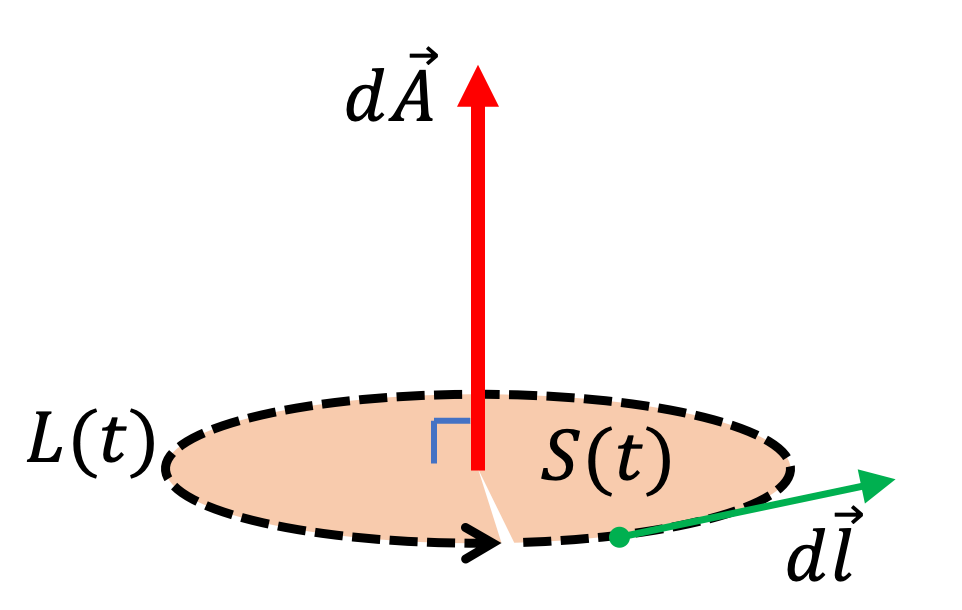
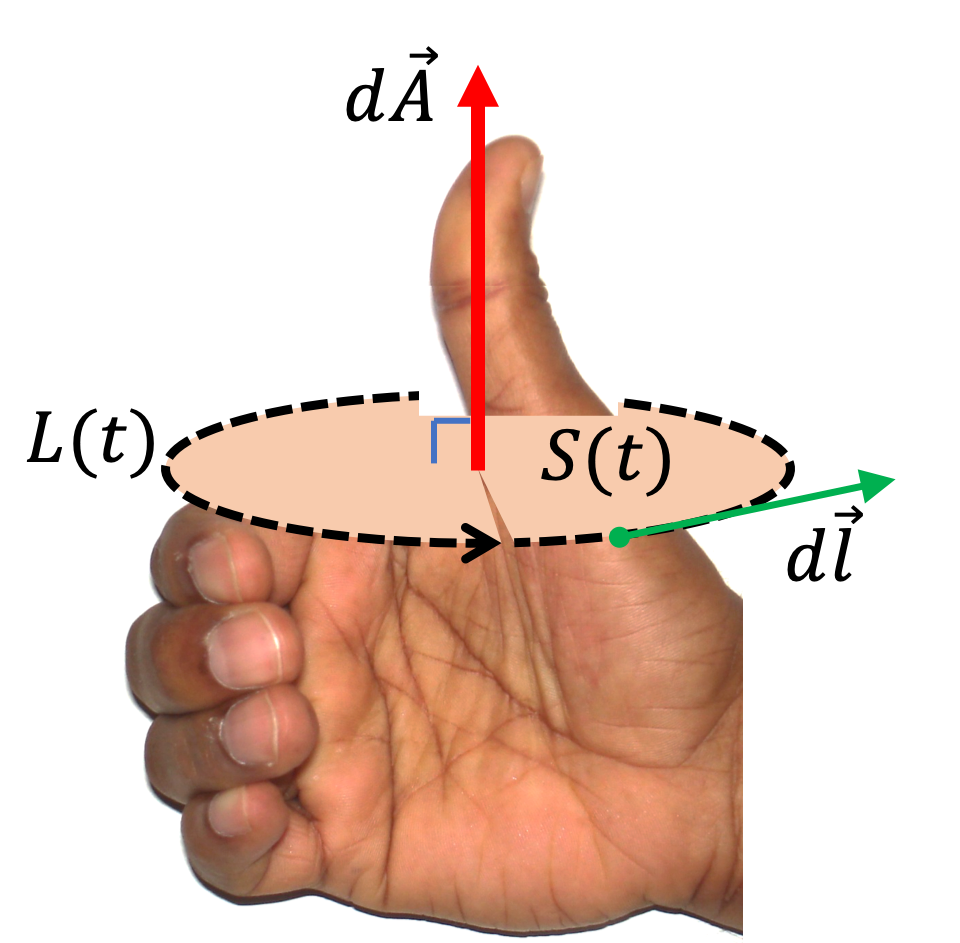
To include the direction information, we cast the circulation and magnetic flux in terms of components. The right-hand rule for Faraday’s law shows that, if the direction of the loop for the circulation is taken along \(\hat u_{\phi}\text{,}\) then the direction of the area element will be towards the positive \(z\)-axis as shown in Figure 38.43. This will give the following for the \(\phi\)-component of electric field.
\begin{equation*}
\left(2\pi r\right) E_{\phi} = -\left( \mu_0 \dfrac{dI}{dt} n \right) \left( \pi a^2\right),
\end{equation*}
where the minus sign on the right side comes from the minus sign in the Faraday’s law. Solving for \(E_{\phi}\) we find
\begin{equation*}
E_{\phi} = -\dfrac{\mu_0 n a^2}{2r}\dfrac{dI}{dt}.
\end{equation*}
Therefore, the electric field induced at a point P outside the solenoid is
\begin{equation*}
\vec E_P = -\dfrac{\mu_0 n a^2}{2r}\dfrac{dI}{dt} \hat u_{\phi}.
\end{equation*}
We find that the induced electric field at the space point P circulates clockwise for an increasing current \((dI/dt>0)\) and counter-clockwise for a decreasing current \((dI/dt\lt 0)\text{.}\) If you place a circular metal wire of radius \(r\) which coincides with the Amperian loop for the circulation of \(\vec E\) calculation, you will notice that there is an induced current in the direction of the induced electric field. Also, if you place a charge anywhere outside the solenoid, the charge will experience an electric force in the axial direction when the current in the solenoid is changing, but no such force when the current in the solenoid is steady.
The result obtained here implies a rather strange conclusion: the electric field at a point outside of a solenoid with a time-varying current is not zero, although the magnetic field there is zero! Note that this takes place only when the current in the solenoid is changing; once the current has become steady, there would be no electric field outside the solenoid.
Electric field inside solenoid
To find electric field induced at a point inside the solenoid we will choose Amperian loop with radius \(r\lt a\) as shown in Figure 38.44.
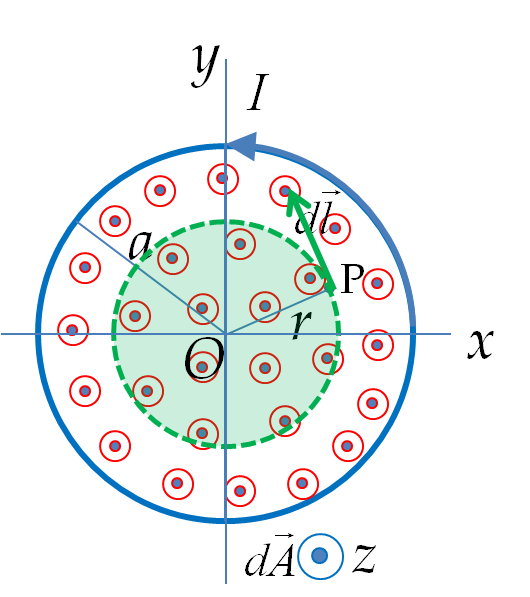
The enclosed magnetic flux will be less than the flux through the entire cross-section of the solenoid - instead, the magnetic flux through only an area \(\pi r^2\) will be enclosed within the Amperian loop. This gives the electric field that increases with the distance from the axis inside the solenoid.
\begin{equation*}
\vec E_P = -\dfrac{\mu_0 n r}{2}\dfrac{dI}{dt} \hat u_{\phi}\ \ \text{(at a point P inside)}.
\end{equation*}