Thermal Area Expansion

Section 20.2 Thermal Area Expansion

When a solid plate is heated, both its length and width expand by the mechanism of linear expansion. Consequently, area change \(\Delta A\) is proportional to the original area \(A\) and rise in temperature \(\Delta T\) assuming \(\Delta A\lt\lt A\text{.}\)

\begin{equation} \Delta A = k A \Delta T.\tag{20.2} \end{equation}

The constant of proportionality \(k\) can be related to the coefficient of linear expansion \(\alpha\) of the material as we can find by considering area change of a rectangular plate of length \(L\) and width \(W\text{.}\)

\begin{equation*} \Delta A = L_0W_0(1+\alpha\Delta T)^2 - L_0W_0 \approx 2\alpha A_0\Delta T. \end{equation*}

With \(A \text{ (at }T+\Delta T \text{)} = (L+\Delta L) (W+\Delta L) \) and \(A \text{ (at }T \text{)} = LW \text{,}\) we get

\begin{align*} \Delta A \amp = A \text{ (at }T+\Delta T \text{)} - A \text{ (at }T \text{)},\\ \amp = \left( LW + L \Delta W + W \Delta L + \Delta L \Delta W\right) - LW, \\ \amp = L \Delta W + W \Delta L + \Delta L \Delta W, \\ \amp \approx L \Delta W + W \Delta L, \end{align*}

where I dropped the last term since it will be considerably smaller than the terms kept. Now, we express the \(\Delta L = \alpha L\Delta T\) and \(\Delta W = \alpha W\Delta T\) to get

\begin{equation} \Delta A = 2\alpha A \Delta T.\tag{20.3} \end{equation}

Hence, the coefficient of area expansion is equal to twice the coefficient of linear expansion.

\begin{equation} k = 2\alpha.\tag{20.4} \end{equation}

Note that the coefficient of expansion for the area is not the square of the coefficient of the linear expansion, i.e. \(k\ne \alpha^2\text{,}\) but rather \(k =2 \alpha\text{.}\) You would make this mistake if you wrongly assumed that \(\Delta A = \Delta L \Delta W \text{ (WRONG!)}\text{.}\)

Example 20.7. Expansion of Copper Plates When Heated.

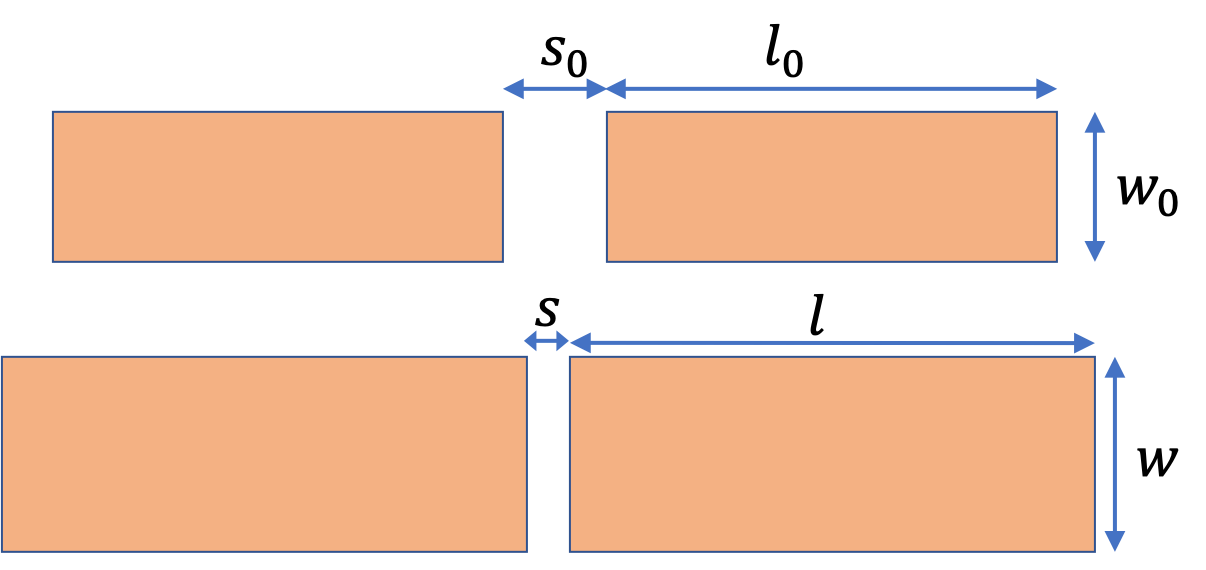
Two copper plates each of length \(l_0 = 15\text{ cm}\) and width \(w_0 = 2\text{ cm}\) at temperature \(25^{\circ}\text{C}\) are placed parallel lengthwise on a wooden plank as shown in the figur below. There is a separation of \(s_0 = 2\text{ cm}\) from one edge of one plate to the nearest edge of the other plate. They are then placed in an oven and heated to a temperature of \(85^{\circ}\text{C}\text{.}\) What is the separation \(s\) between the plates at that temperature? (Ignore any change in the wooden plank.)

Answer.

\(1.985\text{ cm}\)

Solution.

The length expands linearly as does the width. The separation reduces due to expansion along the length. Each plate will expand by \(\Delta l = l - l_0\text{,}\) half of which will come from each plate will reduce the gap between the plates. Therefore, expansion of the two plates together will reduce the distance be \(\Delta l\text{.}\)

Using the coefficient of linear expansion of copper we obtain

\begin{align*} \Delta l \amp = \frac{16.5\times 10^{-6}}{\ ^{\circ}\text{C}}\times 0.15\ \text{m} \times (85-25)^{\circ}\text{C} = 0.15 \ \text{mm}. \end{align*}

Therefore, the separation will be \(2.0\text{ cm} - 0.015\text{ cm} = 1.985\text{ cm}\text{.}\)

Exercises Exercises

1. Expansion of Copper Plates with a rectangular hole When Heated.

A copper plate of length \(l_0 = 15\text{ cm}\) and width \(w_0 = 6\text{ cm}\) with a rectangular hole of length \(l_0 = 10\text{ cm}\) and width \(w_0 = 2\text{ cm}\) at temperature \(25^{\circ}\text{C}\) is placed in an oven and heated to a temperature of \(85^{\circ}\text{C}\text{.}\) How big is the hole at \(85^{\circ}\text{C}\text{?}\)

Hint.

Hole will expand as if it was filled with the same material

Answer.

Hole: \(\Delta l = 0.01\text{ cm}\text{,}\) \(\Delta w = 0.002\text{ cm}\text{.}\)

Solution.

Since the plate is free to expand outward, the plate will expand as if there was no hole, expanding the area of the hole proportionately. The length and width of the hole after expansion will be

\begin{align*} l \amp = 10\text{ cm } + \frac{16.5\times 10^{-6}}{\ ^{\circ}\text{C}}\times 10\ \text{cm} \times (85-25)^{\circ}\text{C}, \\ \amp = 10\text{ cm } + 0.01 \text{ cm}. \\ w \amp = 2\text{ cm } + 0.002 \text{ cm}. \end{align*}

2. Fitting Rivets into Holes by Cooling the Rivets.

For a tighter fit, rivets are usually made slightly larger than the rivet holes, and, to make the rivets fit into the holes, they are cooled before being driven in the holes. Consider a rivet hole of diameter \(4\text{ mm}\) at \(20^{\circ}\text{C}\text{.}\) What would be the diameter of an aluminum rivet at \(20^{\circ}\text{C}\) which just fits the rivet hole when it is cooled by dry ice (solid \(\text{CO}_2\)) to a temperature of \(-78^{\circ}\text{C}\text{?}\)

Data: \(\alpha = \frac{16.5\times 10^{-6}}{\ ^{\circ}\text{C}} \text{.}\)

Hint.

Diameter will expand as length.

Answer.

\(4.0065\text{ mm}\text{.}\)

Solution.

The linear dimension, such as diameter \(D\text{,}\) expands or contracts as length.

\begin{equation*} \dfrac{\Delta D}{D} = \alpha \Delta T. \end{equation*}

Let \(x\) be the diameter of the rivet at \(20^{\circ}\text{C}\text{,}\) whose diameter at \(-78^{\circ}\text{C}\) would have to be \(4\text{ mm}\text{,}\) actually a smidgen less in order to slide through. Therefore, we will get the following equation.

\begin{equation*} \dfrac{x - 4 }{4} = \frac{16.5\times 10^{-6}}{\ ^{\circ}\text{C}} \times (20 -(-78)). \end{equation*}

Solving for \(x\text{,}\) we get \(x = 4.0065\text{ mm}\text{.}\)

Prev Top Next