Physics Bootcamp

Subsection 59.10.1 Dicovery of the Cosmic Background Radiation

Immediately after the Big Bang the universe would have been a fiery ball at an enormous temperature and produced a thermalized radiation. This radiation should be all around us and should come with equal intensity from all direction. This radiation is called the \textbf{Cosmic Background Radiation}.\index{Cosmic background radiation} Wien's law states that the maximum of the radiation emitted by a hot body occurs at a wavelength given by

where \(T\) is temperature in Kelvin. The expansion of the space causes all lengths to expand with it. Therefore, the wavelength \(\lambda_{\text{max}}\) of the most intense light would be red shifted, i.e. become longer. Ralph Asher Alpher with Robert Herman predicted in 1948 that the wavelength of the cosmic background at the present time would correspond to the temperature \(T= 5\:\text{K}\text{.}\) Independently, Robert Dicke and Yakov Zel'dovich also came to similar conclusions in the early 1960s. This temperature would give the \(\lambda_{\text{max}}\) value to be

This prediction turns out to be about two times shorter. While physicists at Princeton University was making preparations to observe this radiation, they heard in 1964 from two physicists, Arno Penzias and Robert Wilson who worked for Bell Laboratories in New Jersey, that they had seen a cosmic background radiation at wavelength 7.35 cm, which is not at the peak wavelength predicted above.

While working on a microwave receiver for a satellite communication system, Penzias and Wilson noticed that no matter what they did, they could not get rid of a faint background noise in the signal. After Penzias and Wilson systematically rejected all sources of radio noise they could think of, such as noise coming from New york City, or from bird droppings, and so on, and could not come up with any explanation, they contacted Robert Dicke of Princeton University, who suggested that the noise may be the background radiation expected from the big bang. Because the radiation was in the microwave region of the spectrum, it is called \textbf{cosmic microwave background radiation (CMBR)}.

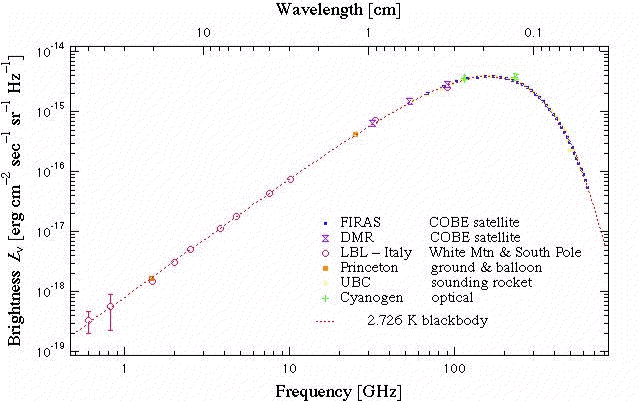
The Penzias and Wilson observation was at a single wavelength, 7.35 cm. The data at other wavelengths were later collected which show a perfect fit to the black body spectrum for a body at temperature \(T=2.726\) K. A modern plot of the intensity at various wavelength and fit to blackbody spectrum from NASA's Cosmic Background Explorer (COBE) mission is displayed in Figure 59.10.1.

Subsection 59.10.2 The Origin of CMR

By tracing back the present condition we can find various phase transitions that must have occurred in the past. Currently, the universe is dominated by matter and has the temperature of 2.7 K. We know two things about the microwave back ground radiation - it is thermal, i.e. blackbody, and it scales with the scale factor \(a\) of the universe. To scale with the scale factor implies that the comoving wavelength has not changed, which would imply that the primordial photons that make up the microwave background have not scattered off particles. When we trace back in time, the universe must have been more compact and hotter in the past. If the temperature of the universe is such that electron and proton would be split by the thermal energy, then, electrons and protons would not be able to form atoms. Locking electrons and protons in atoms makes them less likely to scatter photons. Therefore, the photons we see in the CMB must have separated from the matter at an energy scale which is \(\sim 1\: \text{eV}\text{.}\)

This gives the time when the photons in the CMB last scattered off charged particles was when the time since the big bang was \(380,000\) years. The universe at that time is said to form ``Surface of Last Scattering'' for cosmic photons. Before this time, photons were constantly scattering off charged particles and hence were thermalized. Before this time, the matter in the universe was in the plasma form.

Subsection 59.10.3 Nucleosynthesis of Light Elements

The relative abundances of light elements, Hydrogen, Helium, Lithium, and Beryllium, in the universe provide key evidence for the Big Bang theory. For instance, it turns out that that 25\% of the matter in the universe is He, which is too high an abundance and cannot be explained based on the production of Helium in stars. The data suggests that much of the He in the universe is primordial.

George Gamow asked his student Ralph Alpher in 1948 to find out if all the elements were formed by the Big Bang. The logic was that if you continue the clock backward, the universe will become more and more compressed into smaller and smaller space, getting denser and denser. Eventually, the universe will have high enough temperature for the nuclear synthesis to take place. This occurs with 225 sec of the Big Bang when the temperature of the universe must have been more than \(10^9\text{ K}\text{.}\) The nucleosynthesis during this period is called the Big Bang Nucleosysnthesis.

See the description of the Age of Nucleosyntesis in section Subsection 59.9.2. At first, protons and neutrons combine to form deuteron \(^2\)H, which can capture a neutron to from triton \(^3\)H, which is the nucelus of the radioactive hydrogen called tritium. A deuteron can capture a proton to make helium \(^3\)He. When \(^3\)H captures a proton or \(^3\)He captures a neutron we get helium \(^4\)He. At this stage, the ratio of protons to neutrons was about 7:1. Thus, the process of conversion to \(^4\)He used up almost all neutron. The process lasted about 3 minutes and almost 25\% of all the matter turned into \(^4\)He along with small percent in \(^2\)H, \(^3\)H, and \(^3\)He. Tiny amounts of \(^7\)Li and \(^7\)Be were also made. The expansion during this time cooled the universe enough that the nuclear reactions stopped.

The abundance of the light nuclei, \(^2\)H, \(^4\)He, and \(^7\)Li, except for \(^3\)He, created after the big bang are very dependent on the matter density. Once we determine the matter density, the predicted abundances provide a very stringent test of the big bang and the nuclear synthesis reactions. When the latest reading of the matter density from Wilkinson Microwave Anisotropy Probe (WMAP) is used, the predicted abundances and the observed abundances match very well providing another evidence in favor of the big bang theory.