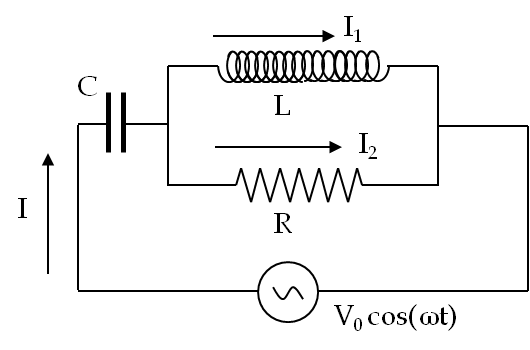
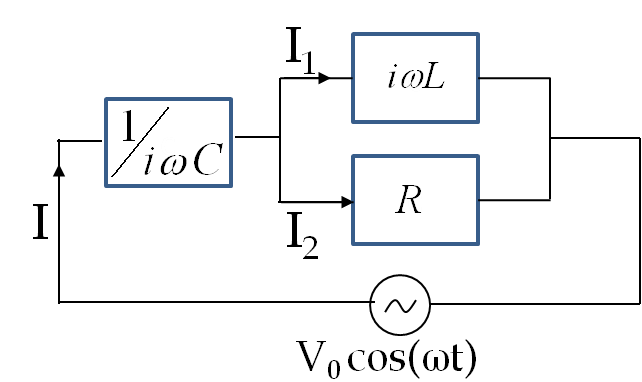
Example 41.42. Series RLC Circuit in Complex Notation.
Consider the series RLC-circuit. Find current in the circuit.
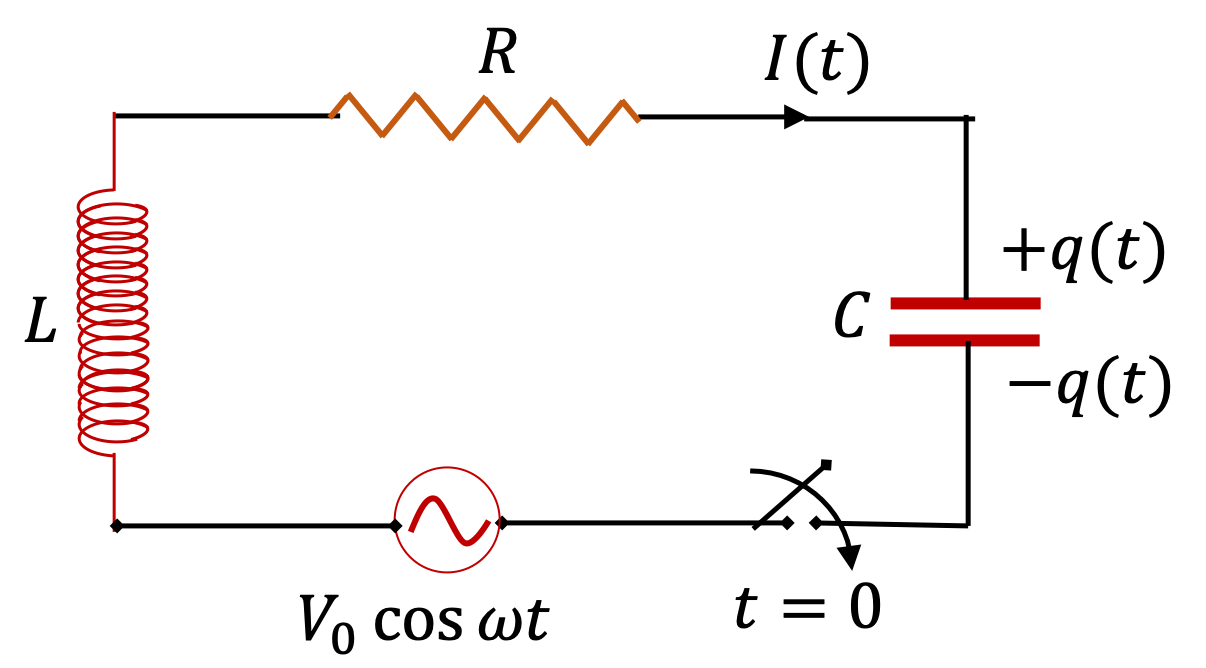
Answer.
\(I_0 = \dfrac{V_0}{ \sqrt{ R^2 + \left( \omega L- \dfrac{1}{\omega C}\right)^2 } }\text{,}\) \(\phi_I = - \tan^{-1} \left( \dfrac{\omega L- \dfrac{1}{\omega C}}{R} \right)\text{.}\)
Solution.
First step in our solution is to replace original circuit by a complex circuit where we replace \(R\) by \(Z_R\text{,}\) \(C\) by \(Z_C\text{,}\) and \(L\) by \(Z_L\text{,}\) and treat currents and voltages complex. This is shown as a complex circuit in the figure below.
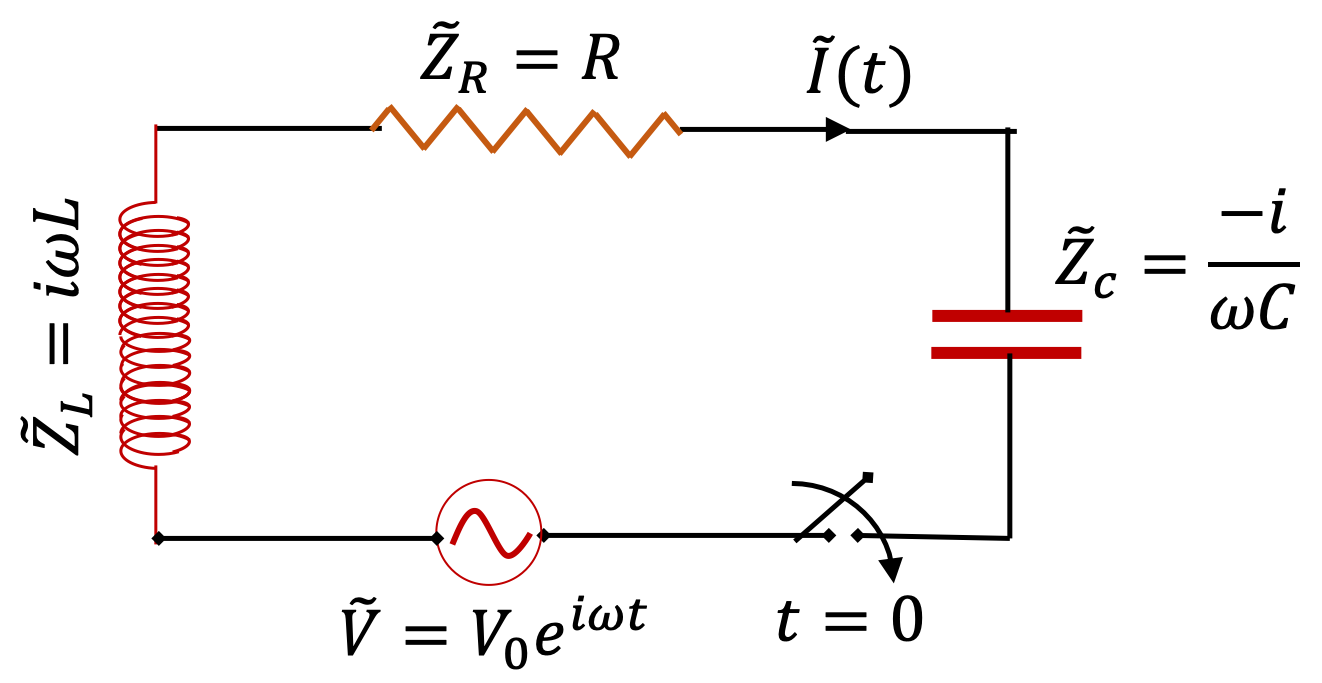
Now, we think of impedances as if they were simple resistors. In this circuit, the loop equation will give
\begin{equation*}
\tilde V - \tilde Z_R\tilde I - \tilde Z_L\tilde I - \tilde Z_C\tilde I = 0,
\end{equation*}
which can be solved for complex current.
\begin{equation}
\tilde I = \dfrac{\tilde V}{ \tilde Z_R + \tilde Z_L + \tilde Z_C}.\tag{41.43}
\end{equation}
From this we note that complex impedance of the circuit is
\begin{align*}
\tilde Z \amp = \tilde Z_R + \tilde Z_L + \tilde Z_C \\
\amp = R + i \omega L+ \dfrac{-i}{\omega C} \\
\amp = R + i \left( \omega L- \dfrac{1}{\omega C}\right)
\end{align*}
This is rectangular form of complex impedance, which we can also write in polar form. Let
\begin{equation*}
R + i \left( \omega L- \dfrac{1}{\omega C}\right) = |Z|\,e^{i\phi_Z}.
\end{equation*}
Then,
\begin{gather*}
|Z| = \sqrt{ R^2 + \left( \omega L- \dfrac{1}{\omega C}\right)^2 } \\
\phi_Z = \tan^{-1} \left( \dfrac{\omega L- \dfrac{1}{\omega C}}{R} \right)
\end{gather*}
Using polar form of complex impedance in Eq. (41.43) we get polar form of complex current.
\begin{equation*}
\tilde I = \dfrac{\tilde V}{ \tilde Z } = \dfrac{V_0}{|Z|}\, e^{i\left(\omega t-\phi_Z\right)},
\end{equation*}
whose real part gives the physical current in the circuit.
\begin{equation*}
I(t) = \dfrac{V_0}{|Z|}\,\cos(\omega t - \phi_Z ).
\end{equation*}
Wrting this as \(I(t) = I_0\,\cos(\omega t + \phi_I)\) we have
\begin{gather*}
I_0 = \dfrac{V_0}{ \sqrt{ R^2 + \left( \omega L- \dfrac{1}{\omega C}\right)^2 } },\\
\phi_I = - \tan^{-1} \left( \dfrac{\omega L- \dfrac{1}{\omega C}}{R} \right).
\end{gather*}