We found in our last chapter that we can separate translational motion of the center of mass motion and motion about the center of mass by replacing velocity \(\vec v_i\) by sum of velocity \(\vec v'_i\) with respect to CM and velocity \(V_\text{cm}\) of the CM.
\begin{equation*}
\vec v_i = \vec V_\text{cm} + \vec v'_i.
\end{equation*}
The calculation of separation gives
\begin{align*}
K_\text{tot} \amp = \frac{1}{2}\sum_{i}m_i v_i^2 = \frac{1}{2}\sum_{i}m_i \vec v_i \cdot \vec v_i \\
\amp = \frac{1}{2}\sum_{i}m_i (\vec V_\text{cm} + \vec v'_i) \cdot (\vec V_\text{cm} + \vec v'_i) \\
\amp = \frac{1}{2}\vec V_\text{cm} \cdot \vec V_\text{cm} \sum_{i}m_i +
\vec V_\text{cm}\cdot \sum_{i}m_i \vec v'_i + \frac{1}{2}\sum_{i}m_i\vec v'_i\cdot \vec v'_i \\
\amp = \frac{1}{2} M V_\text{cm}^2 + \frac{1}{2}\sum_{i}m_i\vec v'_i\cdot \vec v'_i.
\end{align*}
In the last step I used the fact that \(\sum_{i}m_i \vec v'_i=0\) since \(\vec v'_i\) are velocities with respect to the CM and have replaced total mass by \(M\text{.}\) The first part is kinetic energy of translation of the CM and the second part is the rotational kinetic energy.
\begin{align}
\amp K_\text{cm} = \frac{1}{2} M V_\text{cm}^2. \tag{10.32}\\
\amp K_\text{rot} = \frac{1}{2}\sum_{i}m_i\vec v'_i\cdot \vec v'_i. \tag{10.33}
\end{align}
By making use of the relation, \(\vec v' = \vec\omega \times \vec r'\text{,}\) for each particle, we can write \(K_\text{rot}\) in terms of angular velocity and angular moementum. Thus,
\begin{align*}
K_\text{rot} \amp = \frac{1}{2}\sum_{i}m_i\vec v'_i\cdot \vec v'_i\\
\amp = \frac{1}{2}\sum_{i}m_i(\vec\omega \times \vec r'_i)\cdot (\vec\omega \times \vec r'_i)\\
\amp = \frac{1}{2}\sum_{i}m_i\vec\omega \cdot [ \vec r'_i \times (\vec\omega \times \vec r'_i)]\\
\amp = \frac{1}{2}\vec\omega \cdot \sum_{i}m_i [ \vec r'_i \times (\vec\omega \times \vec r'_i)] .
\end{align*}
The expression
\(\sum_{i}m_i [ \vec r'_i \times (\vec\omega \times \vec r'_i)]\) is angular momentum
\(\vec L\) about CM by
(10.9). Therefore,
\begin{equation}
K_\text{rot} = \frac{1}{2}\,\vec\omega \cdot \vec L.\tag{10.34}
\end{equation}
We can replace \(\vec L\) by \({\bf I}\vec \omega\text{,}\) where \({\bf I}\) is full moment of inertia, giving us
\begin{equation}
K_\text{rot} = \frac{1}{2}\,\vec\omega \cdot ( {\bf I}\vec \omega ).\tag{10.35}
\end{equation}
We know that \({\bf I}\) simplifies when we use principal axes of the rotating body. Therefore, in a coordinate system along principal axes we can write kinetic energy in terms of components of angular velocity as
\begin{equation}
K_\text{rot} = \frac{1}{2} I_{xx}\omega_x^2 + \frac{1}{2} I_{yy}\omega_y^2 + \frac{1}{2} I_{zz}\omega_z^2.\tag{10.36}
\end{equation}
Often, it is useful to think of this relation in terms of angular momentum components rather than angular velocity components. Since in principal axes, \(L_{i} = I_{ii}\omega_i\) for \(i=x,y,z\text{,}\) rotational kinetic energy can also be written as
\begin{equation}
K_\text{rot} = \frac{1}{2} \frac{L_x^2}{I_{xx}} + \frac{1}{2} \frac{L_y^2}{I_{yy}} + \frac{1}{2} \frac{L_z^2}{I_{zz}}. \tag{10.37}
\end{equation}
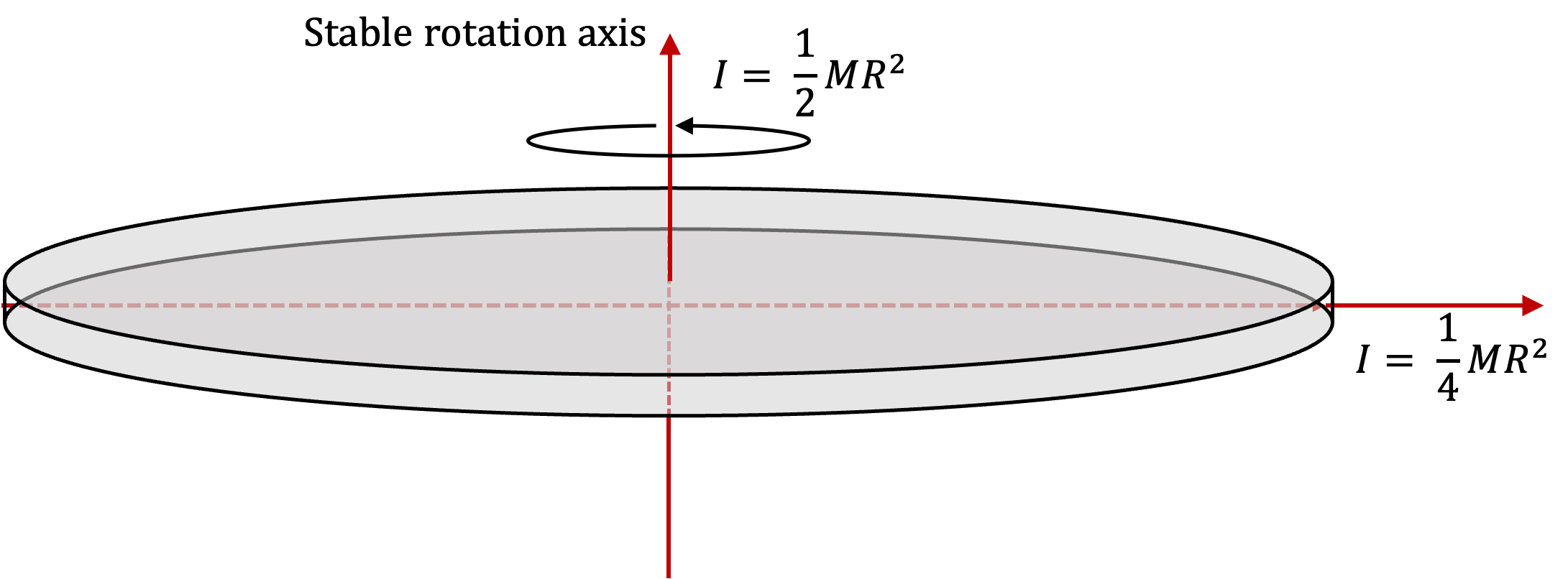
From this expression of \(K_\text{rot}\text{,}\) we can see that the principal axis about which moment of inertia is largest would tend to minimize kinetic energy. This leads to more stability for rotations around principal axis of largest \(I\text{.}\) If you start a rotation around an axis that has smallest moment of inertia, then, over time, the body will wobble and tend to settle in rotation about axis of largest moment of inertia.