Skip to main content

Section 8.4 The Work-Energy Theorem

Subsection 8.4.1 Kinetic Energy and Net Work

Consider the motion of the body over an interval from \(t_i \) to \(t_f\text{.}\) Let \(K_i \) be its kinetic energy at the initial time and \(K_f \) at the final time. That is,

\begin{equation*} K_i = \dfrac{1}{2}\, m\, v_i^2,\ \ \ K_f = \dfrac{1}{2}\, m\, v_f^2, \end{equation*}

where \(v_i\) and \(v_f \) are the speeds at the initial and final instants.

Using Newton's second law of motion, we can prove the following important equality.

\begin{equation} W_{if}^{\text{net}} = K_f - K_i,\tag{8.4.1} \end{equation}

where \(W_{if}^{\text{net}} \) is the net work done by all the forces during the interval \(t_i \) to \(t_f\text{.}\) This result is called the Work-energy theorem. It says that if there is no net work, then kinetic energy would not change. You might think of this as a statement of the conservation of kinetic energy.

No change in kinetic energy if no work done!

A box of mass \(20\text{ kg}\) is pushed on a floor with a constant horizontal force of \(50\text{ N}\text{.}\) There is a kinetic friction of magnitude \(10\text{ N}\) that opposes the sliding of the box. The weight of the box is balanced by the normal force.

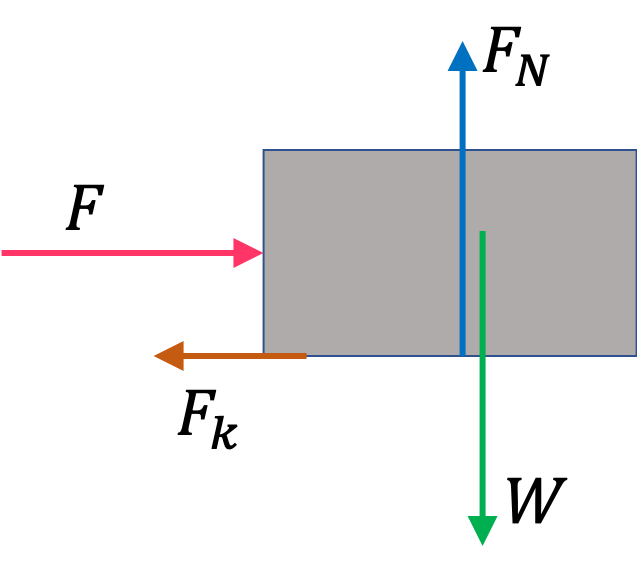
(a) How much work is done on the box by each of the forces when the box is displaced by \(3.0 \text{ m}\text{?}\)

(b) How much net work is done on the box when box is displaced by \(3.0 \text{ m}\text{?}\)

(c) How much kinetic energy of the box changes when it is displaced by \(3.0 \text{ m}\text{?}\)

(d) If the speed of the box was \(2.0\text{ m/s} \) at the beginning of the interval, what will be its speed at the end?

Hint

Answer

(a) \(150\text{ N.m}\text{,}\) \(-30\text{ N.m}\text{,}\) 0, 0, (b) \(120\text{ N.m}\text{,}\) (c) \(120\text{ J}\text{,}\) (d) \(4\text{ m/s}\text{.}\)

Solution 1 (a)

(a) The push force \(\vec F\) is in the direction of the displacement. Therefore, work by this force will be

\begin{equation*} W_{if}^{F} = 50\text{ N}\times 3.0 \text{ m}\times \cos\, 0^{\circ} = 150\text{ N.m}. \end{equation*}

The kinetic friction \(\vec F_k\) acts in the opposite direction of motion, and hence to displacement. Therefore,

\begin{equation*} W_{if}^{F_k} = 10\text{ N}\times 3.0 \text{ m}\times \cos\, 180^{\circ} = -30\text{ N.m}. \end{equation*}

Work by other forces, weight and normal, are zero, since they are perpendicular to the displacement.

Solution 2 (b)

(b) We add work by all forces to get he net work.

\begin{equation*} W_{if}^{\text{net}} = W_{if}^{F} + W_{if}^{F_k} = 150\text{ N.m} - 30\text{ N.m} = 120\text{ N.m}. \end{equation*}
Solution 3 (c)

(c) According the work-energy theorem, the change in kinetic energy is equal to the net work.

\begin{equation*} \Delta K = W_{if}^{\text{net}} = 120\text{ N.m}. \end{equation*}

But, when we write units of \(K \text{,}\) we reexpress the unit as

\begin{equation*} \text{kg.m}^2\text{/s}^2 \text{ or } \text{J}, \end{equation*}

which is equal to \(\text{N.m} \text{.}\)

\begin{equation*} \Delta K = 120\text{ J}. \end{equation*}
Solution 4 (d)

(d)

From the change in kinetic energy, we can find the speed at the end if we know the speed at the beginning. We have,

\begin{equation*} \dfrac{1}{2}\,m\,v_f^2 - \dfrac{1}{2}\,m\,v_i^2 = W_{if}^{\text{net}}. \end{equation*}

Rearranging we get

\begin{equation*} v_f^2 = v_i^2 + \dfrac{2}{m}\times W_{if}^{\text{net}}. \end{equation*}

Putting in the numbers gives

\begin{equation*} v_f^2 = 2.0^2 + \dfrac{2}{20}\times 120 = 16. \end{equation*}

Taking square root and keeping only the positive root (since speed by definition is positive), we get

\begin{equation*} v_f = 4\text{ m/s}. \end{equation*}

The speed of a train of mass \(20,000\text{ kg}\) changes from \(5 \text{ m/s}\) to \(10 \text{ m/s}\) over a distance of \(200\text{ m}\text{.}\) What is the average net force on the train?

Hint

Use \(F_\text{av} d = \Delta KE \text{.}\)

Answer

\(3,750\text{ N} \text{.}\)

Solution

Since the train is accelerating, the average net force will be in the direction of the motion of the train. Let \(F_\text{av}\) be the magnitude of this force. The work done by this force over a displacement \(d \) will be

\begin{equation*} W = F_\text{av} d, \end{equation*}

which will equal the change in the kinetic energy. Therefore, we will have

\begin{equation*} F_\text{av} d = \Delta KE. \end{equation*}

Solving this we get

\begin{equation*} F_\text{av} = \dfrac{1}{d}\, \Delta KE. \end{equation*}

Now, we use numerical values given.

\begin{equation*} \Delta KE = \dfrac{1}{2} m v_f^2 - \dfrac{1}{2} m v_i^2 = 750,000\text{ J}. \end{equation*}

Therefore

\begin{equation*} F_\text{av} = \dfrac{750,000}{200} = 3,750\text{ N}. \end{equation*}

Subsection 8.4.2 (Calculus) Work-Energy Theorem

We will now prove the work-energy theorem stated above using a simple system. Let us consider the simplest possible system - a system that has a single particle of fixed mass \(m \text{,}\) that is subject to a net force, \(\vec F_{\text{net}}\text{.}\) Newton's second law in Force/acceleration form is as follows.

\begin{equation*} \vec F_{\text{net}} = m\dfrac{d\vec v}{dt} \end{equation*}

Now, we take a dot product of both sides with the infinitesimal displacment vector \(d\vec r\) and integrate over a path during an interval \(t_i\) to \(t_f\text{.}\) The force side of this eqaution gives the net work by all forces, but what about the right side?

\begin{align*} \int_i^f\,\vec F_{\text{net}}\cdot d\vec r \amp = \int_i^f\,m\,\dfrac{d \vec v}{dt}\cdot d\vec r = \int_i^f\,m\, (d \vec v) \cdot \dfrac{d\vec r}{dt} \\ \amp = \int_i^f\,m\, (d \vec v) \cdot \vec v = \int_i^f\,m\, \vec v \cdot d \vec v\\ \amp = \int_i^f\,m\, (v_xdv_x + v_ydv_y + v_zdv_z) \\ \amp = m\,\int_i^f\, \left( \dfrac{1}{2}dv_x^2 + \dfrac{1}{2}dv_y^2 + \dfrac{1}{2}dv_z^2 \right) \\ \amp = \dfrac{m}{2}\,\int_i^f\, d\left( v_x^2 + v_y^2 + v_z^2 \right) = \dfrac{m}{2}\,\int_i^f\, dv^2 \\ \amp = \dfrac{1}{2} m \,\left( v_f^2 - v_i^2\right) = K_f - K_i, \end{align*}

where \(v_i \) and \(v_f \) are the initial and final speeds. The left side is just the total work done and the right side the change in kinetic energy.

\begin{equation} W_{if}^{\text{net}} = K_f - K_i.\label{eq-work-energy-theorem-0}\tag{8.4.2} \end{equation}

You might say that: But, you have proven work-energy theorem for a system of one particle only. How do I know it works in general?

Well, lets see what will happen to a system of arbitray number of particles. Each particle will have its own equation of motion given by Newton's second law applied to that particle. Using obvious notation to denote quantities, we will get the following collection of equations.

\begin{align*} \amp \vec F_{\text{on 1}} = m_1 \dfrac{d\vec v_1}{dt}, \\ \amp \vec F_{\text{on 2}} = m_2 \dfrac{d\vec v_2}{dt}, \\ \amp \vec F_{\text{on 3}} = m_3 \dfrac{d\vec v_3}{dt}, \\ \amp \cdots \end{align*}

where the forces on each particle are the net force on that particle, that include forces from other particles in the system, and objects that are not part of the system.

Now, we take dot product of first equation with \(d\vec r_1\) where \(\vec r_1\) is the position of particle 1. And, do similarly, for the other equations. Each equation can then be processed as we have done for the one-particle calculation above. These will give us

\begin{align*} \amp W_{\text{on 1}} = K_{1,f} - K_{1,i}, \\ \amp W_{\text{on 2}} = K_{2,f} - K_{2,i}, \\ \amp W_{\text{on 3}} = K_{3,f} - K_{3,i}, \\ \amp \cdots \end{align*}

Now summing all these will give us

\begin{equation*} W_{if}^{\text{all}} = K_f^{\text{all}} - K_i^{\text{all}}. \end{equation*}

This shows that the work-energy theorem is applicable to systems containing any number of particles. The work must include work by forces between particles of the system as well as by forces between the system and the external world. Unlike the impulse/momentum of multiparticle system, the work by internal forces do not necessarily cancel out here.