Physics Bootcamp

A thermodynamic state of a system is specified by the macroscopic properties of the system such as pressure, volume, temperature, internal energy, enthalpy, and entropy. They correspond to the equilibrium state of a very large number of molecules in any finite size system. On the other hand, a microstate or dynamical state refers to the set of positions and velocities of all the particles of the system, which may be molecules of the system.

It turns out that many different microstates of a system in equilibrium have the same values of the macroscopic properties. Since the number of particles in any finite size system is too large to know the microstates, physicists have developed statistical methods for extracting the macroscopic variables from averages over the microstates. The statistical considerations of the distribution of the microstates gives us a deeper understanding of the values of macroscopic variables.

Let \(n_1\text{,}\) \(n_2\text{,}\) etc. be the number of microstates that correspond to thermodynamic states labeled \(X_1\text{,}\) \(X_2\text{,}\) etc. respectively. For instance, when the system is in any one of the \(n_1\) microstates of state \(X_1\text{,}\) it has particular values of temperature \(T_1\text{,}\) pressure \(p_1\text{,}\) volume \(V_1\) and other macro properties. It is possible, in principle, to introduce probabilities of each thermodynamic state based on the relative number of the microstates. Therefore, the probability that a system will be in the thermodynamic state labeled \(X_i\) should be given by

The subject of statistical mechanics deals with the study of thermodynamics in terms of these probabilities that provide the description of a thermodynamic state in terms of microstates. According to statistical mechanics, an isolated system is most likely to be found in a thermodynamic state that has the highest probability. Let \(P\) be the probability for a system to be in a particular thermodynamic state in which the system has the entropy \(S\text{.}\) Ludwig Boltzmann showed that the entropy \(S\) of the state is proportional to the logarithm of probability \(P\text{.}\)

where the proportionality constant \(k_B\) is Boltzmann constant. This result shows that a spontaneous processes of an isolated system will always move the system towards the higher probability states since that would correspond to increasing the entropy as required by the second law of thermodynamics.

For example, consider two chambers connected by a valve as shown in Figure 26.6.1. The number of microstates where all the molecules are in one chamber is considerably less than the number when molecules are distributed in both chambers. When the valve is opened, the gas will distribute into both chambers. Why? In the present view, we compare the number of microstates in the state \#1 the valve is open and all gas is on one side to the number of microstates in the the state \#2 the valve is open and the gas is distributed on both sides. Many more microstates correspond to the distributed state than the state in which all gas is on one side. Therefore, the system will move from state \# 1 to state \# 2.

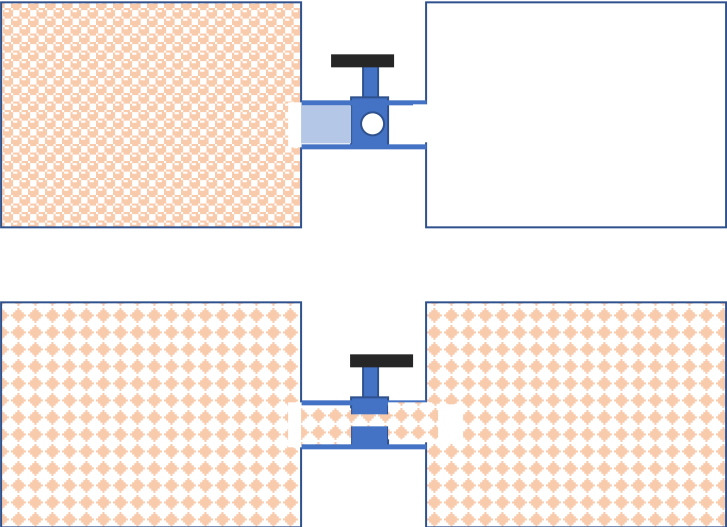
You can show generally that a state where molecules are more disordered has more microstates than the one that is less disordered. Thus, the second law of thermodynamics can be stated yet another way based on the disordered nature of microstates.

An isolated system moves towards the most disordered state.