Consider a shell of fluid between \(r\) and \(r+\Delta r\text{.}\) As shown in the figure the the shell can be thought of a sheet of thickness \(\Delta r\) and area \(2\pi r L\text{.}\) This problem then becomes similar to the problem of heat flow through a window.
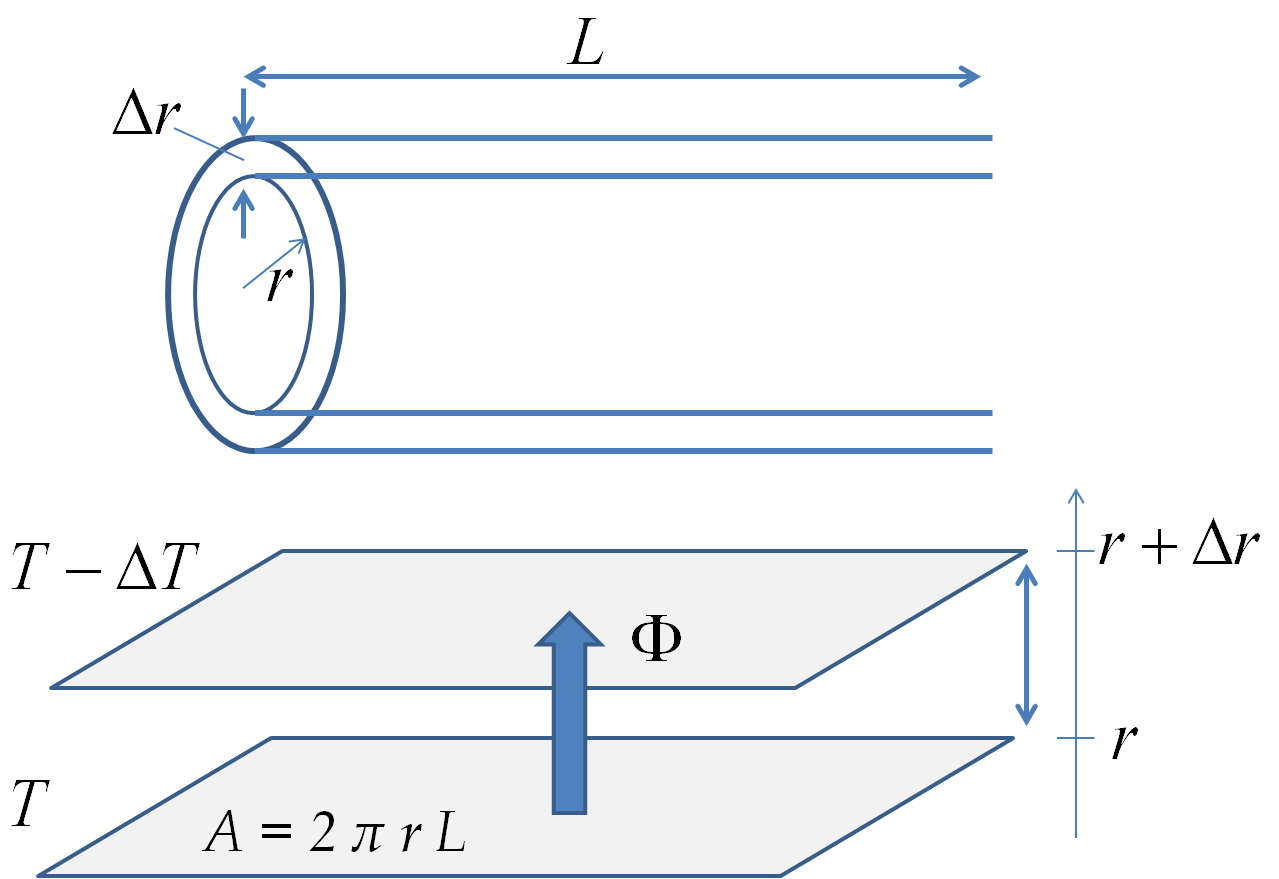
Writing the flux in terms of the rate of flow of heat over the area and in terms of the conductivity we find
\begin{equation*}
\Phi = \frac{\Delta Q/\Delta t}{2\pi r L} = - k \frac{\Delta T}{\Delta r},
\end{equation*}
where the negative sign is there since the heat flows towards larger \(r\text{,}\) i.e. increasing \(r\) corresponds to decreasing \(T\text{.}\) We have taken \(\Delta Q\) positive here. Making the shell infinitesimally thin turns the right side to \(-k dT/dr\text{.}\)
\begin{equation*}
\frac{\Delta Q/\Delta t}{2\pi r L} = - k \frac{d T}{d r}
\end{equation*}
Now, we rearrange terms to separate the $r$ and $T$ on different sides to obtain
\begin{equation*}
\left[ \frac{\Delta Q/\Delta t}{2\pi L} \right] \frac{dr}{r}= - k dT.
\end{equation*}
Integrating from \(r=R_1\) with \(T=T_1\) to \(r=R_2\) with \(T=T_2\) and rearranging gives the desired result.
\begin{align*}
\amp \left[ \frac{\Delta Q/\Delta t}{2\pi L} \right] \int_{R_1}^{R_2}\frac{dr}{r}= - k \int_{T_1}^{T_2}dT,\\
\amp \left[ \frac{\Delta Q/\Delta t}{2\pi L} \right] \ln\left( \frac{R_2}{R_1} \right)
= k \left( T_1-T_2\right),\\
\amp \left[ \frac{\Delta Q/\Delta t}{ L} \right]
= \frac{2\pi k \left( T_1-T_2\right)}{\ln\left( R_2 / R_1 \right)}.
\end{align*}



