Section 47.5 Lenses
In the last section we discussed refraction at a spherical surface. Once a light ray enters the second medium, it will travel in a straight line till it encounters the end of that medium and will refract at this second surface.
Lenses have two surfaces for light to pass through. The two surfaces could be of any type, but in practice, since spherical surfaces are easy to manufacture, most cheap lenses have either both surfaces spherical or one spherical and the other plane. Each surface can be carved to yield a convex or a concave surface. This yields a variety of choices illustrated in Figure 47.5.1.
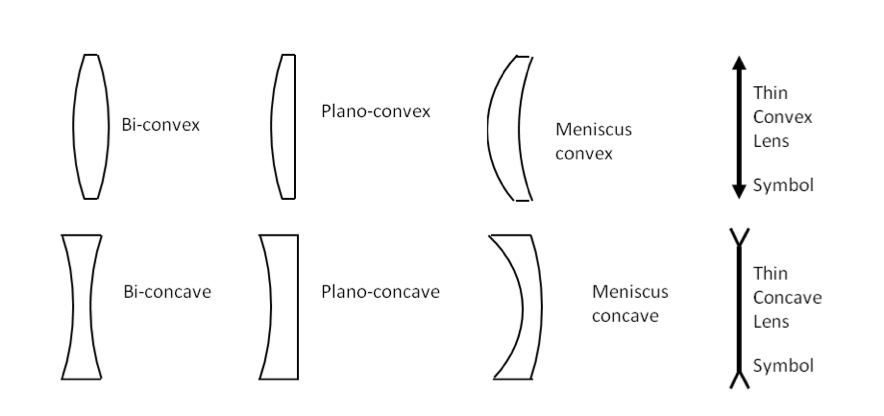
If rays passing through the entire lens bend towards the axis, we say that the lens is a converging lens or convex lens. The term convex lens does not mean both surfaces are convex - it means that overall the lens is a converging lens. On the other hand, if rays bend away from the axis, we say that the lens is a diverging lens or concave lens.
In this section you will some important rays that we encounter when analyzing refraction through lenses. You will also learn about focal length and power of a lens.
Subsection 47.5.1 Special Rays Through a Thin Converging Lens
There are three rays whose behavior is particularly simple. Figure 47.5.2 shows these rays.
- Chief Rays. These rays pass through the center of the lens. These rays represent the fact that near the center of the lens, the lens is like a parallel plate. When we neglect the thickness of this plate, we will get negligible lateral deviation.
- First Focal Point and Emerging Parallel Rays. When rays pass through the first focal point \(F_1\) of the lens, they emerge parallel. The figure illustrates the case where the rays come out parallel to the axis.
- Second Focal Point and Incident Parallel Rays. When rays parallel to the axis strike a converging lens, all of the transmitted rays pass through the second focal point on the axis.
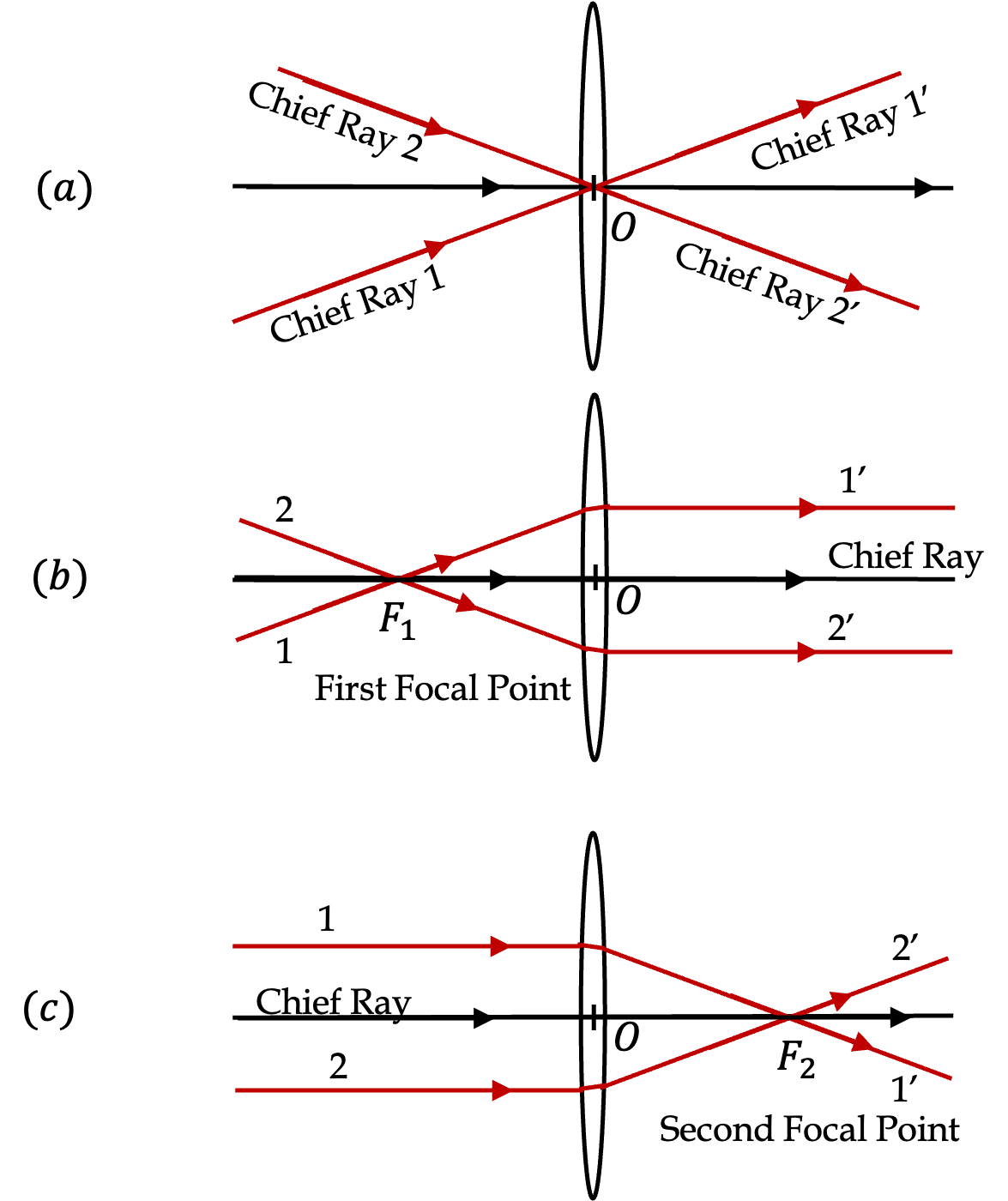
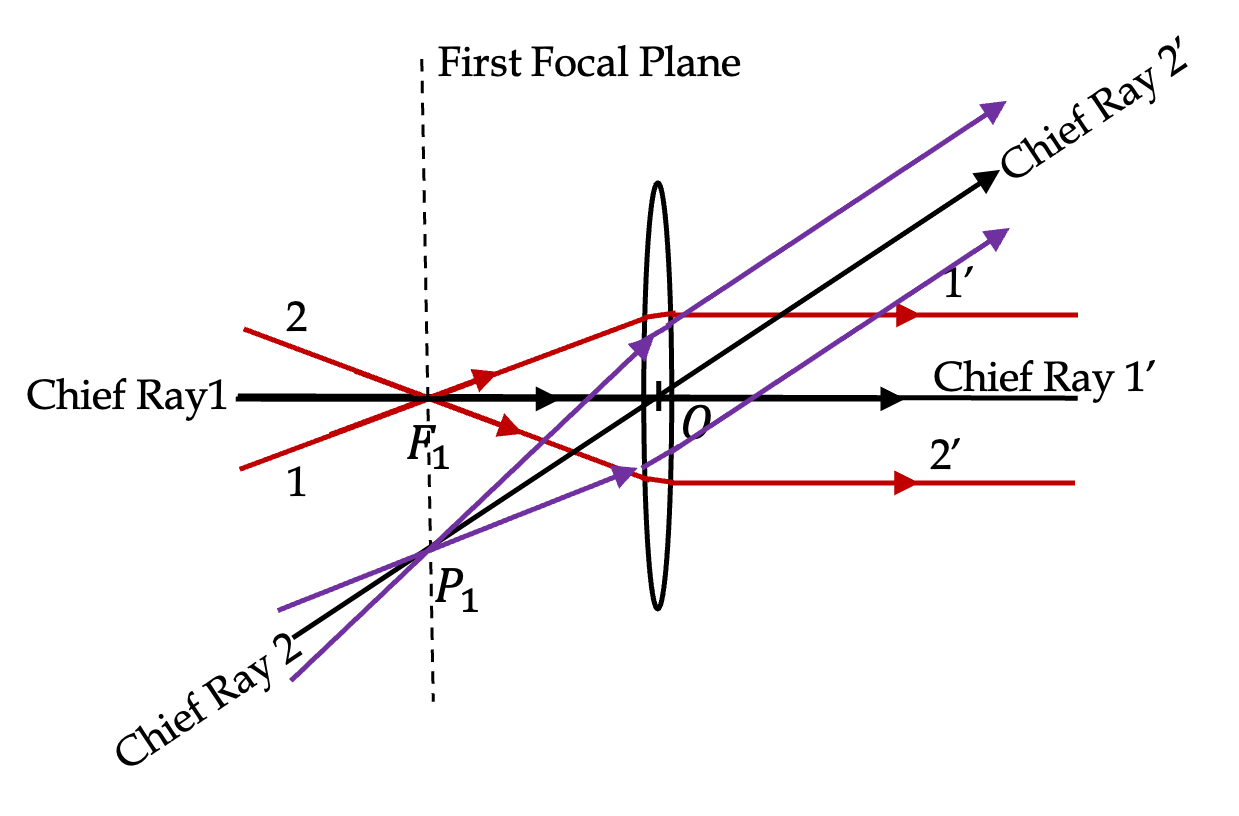
In Figure 47.5.2(b) and (c), the parallel rays are parallel to the axis, which is also the chief ray in that direction. Same behaviour takes place along other chief rays, which are at an angle to the the axis. Figure 47.5.3 illustrates rays that pass through a common point \(P_1\) in the plane, called the first focal plane, that contains the first focal point and is perpendicular to the axis. The emerging rays are parallel to the chief ray in that direction.
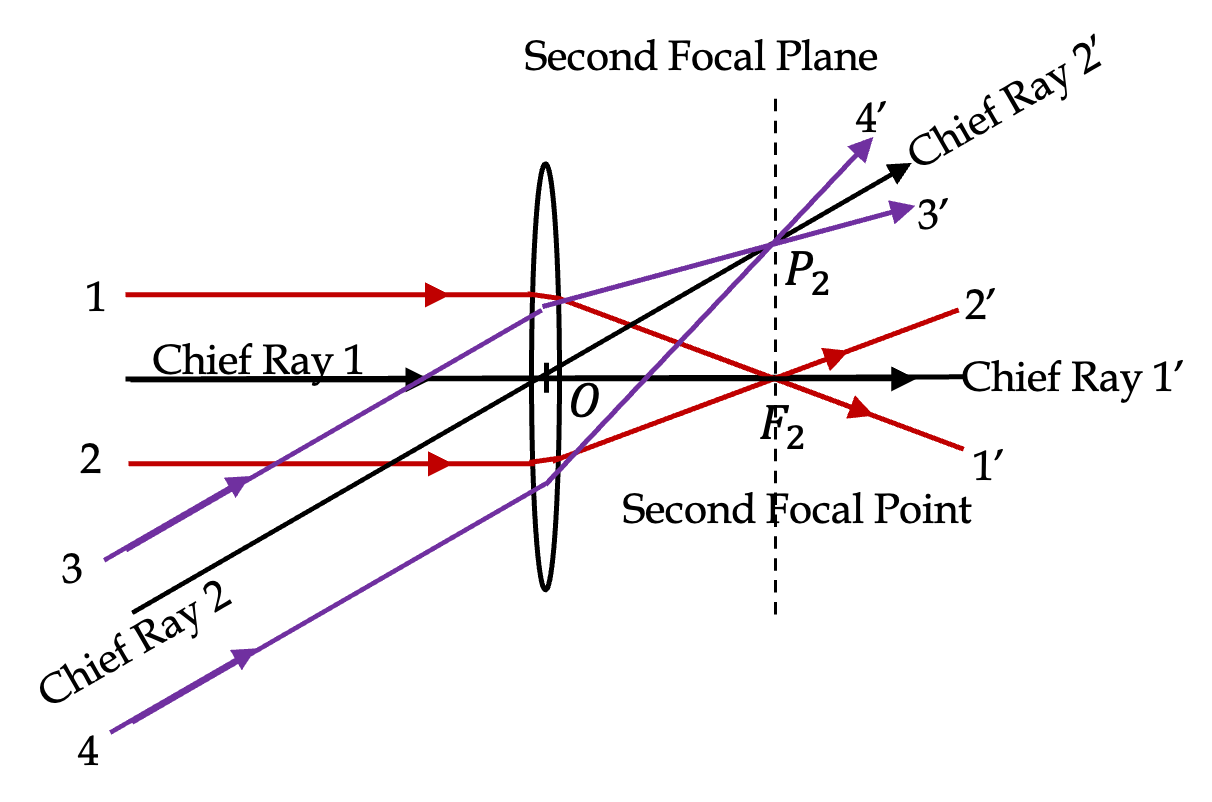
Similarly, if parallel rays in some other direction than the one parallel to the optical axis strike the converging lens, they pass through a common point in a plane containg the second focal point \(F_2\text{.}\) This is shown as point \(P_2\) in Figure 47.5.4.
Subsection 47.5.2 Special Rays Through a Thin Diverging Lens
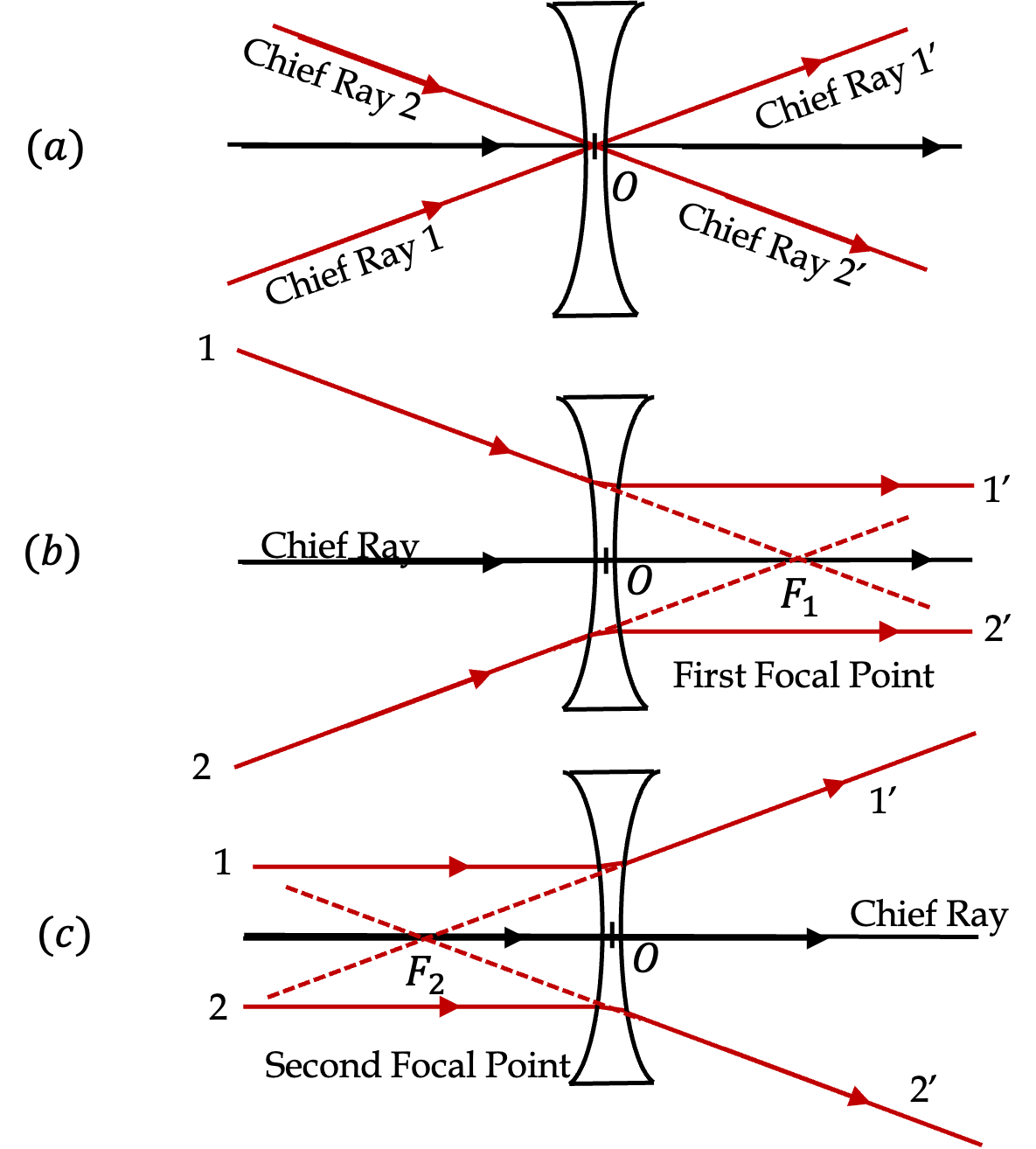
Similar to the convergin lens, there are three rays for diverging lenses corresponding to the rays that go through the center, rays that are parallel as incoming, and those that are parallel outgoing. Figure 47.5.5 shows these rays.
- Chief Rays. These rays pass through the center of the lens. These rays represent the fact that near the center of the lens, the lens is like a parallel plate. When we neglect the thickness of this plate, we will get negligible lateral deviation.
- First focal Point and Incident Parallel Rays. When rays that are parallel to the axis strike a diverging lens, the diverge away from each other on the other side of the lens. When these rays are extended back, they meet at first focal point \(F_1\) at the axis. If you had parallel rays that are at an angle to the axis, they will appear to come from an off-axis point of the first focal plane as we saw for the converging lens.
- Second Focal Point and Emerging Parallel Rays. When rays are pointed towards second focal point on the axis, they emerge parallel to the axis. If rays are pointed at an off-axis point of the second focal plane, i.e., the plane containg \(F_2\) and prependicular to the optical axis, then, the will emergy parallel, but in the direction of the point in the second focal plane. This is similar to what we saw in the converging lens case.
Subsection 47.5.3 Focal Length and Power of Lens
The distance from front vertex of the lens to the first focal point \(\text{F}_1\) is called the first focal length and is usually denoted by \(f_1\text{.}\) Similarly, the distance from back vertex of the lens to the second focal point \(\text{F}_2\) is called the second focal length and is usually denoted by \(f_2\text{.}\) If the lens is thin, the two distances are equal to each other, and we just call the common number the focal length of the lens.
Focal length of a converging lens is denoted by a positive number. This refers to the positive distance on the axis from the lens to the second focal point. Focal length of a diverging lens is denoted by a negative number, which referes to the distance on the axis from the lens to the first focal point. Thus, if you are given that focal length is \(f=-20\text{ cm}\text{,}\) you immediately know that it is a concave lens.
The inverse of the focal length is called power of the lens, which is denoted by \(P\text{.}\)
When focal length is expressed in \(\text{m}\text{,}\) the unit of power of lens is called \(\text{Diopter}\) or \(\text{dpt}\text{.}\) That is \(1\text{ dpt}\) stands for \(1\text{ m}^{-1}\text{.}\)
When we stack multiple lenses, their power adds algebraically. For instance, if you have two lenses of focal lengths \(f_A=-20\text{ cm}\) and \(f_B=5\text{cm}\text{.}\) The combined power will be