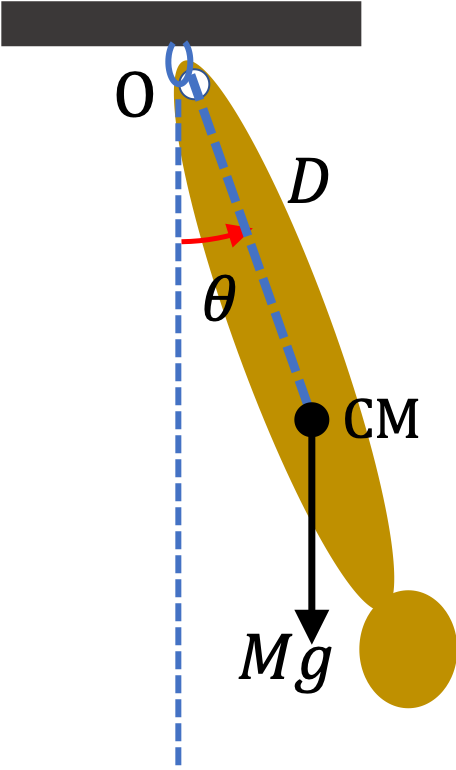
A rigid body hung from a post swings just like a pendulum. Such oscillating bodies are called physical pendulums. We want to find the frequency of small oscillations.
We study oscillations of a physical pendulum in small amgle approximation. Thus, the torque of the weight when the body’s CM is at an angle \(\theta\) with respect to the vertical becomes linear in the angle \(\theta\) as was the case with the plane pendulum.
\begin{equation*}
\tau_\text{net} = - M g D \sin\theta \approx - M g D \theta\ \ (\theta \ll 1\,rad).
\end{equation*}
where the negative sign refers to the clockwise sense of rotation. Let \(I\) be moment of inertia about the axis and \(\alpha\) the angular acceleration. Then, the equation of motion
\begin{equation}
I\alpha = - MgD\theta,\tag{13.34}
\end{equation}
where angular acceleration is
\begin{equation*}
\alpha = \frac{d^2 \theta}{dt^2}.
\end{equation*}
Rewriting the equation of motion as
\begin{equation*}
\frac{d^2 \theta}{dt^2} = - \dfrac{MgD}{I}\,\theta.
\end{equation*}
Comparing this to the equation of motion of a simple harmonic motion, \(a_x = -\omega^2 x \text{,}\) and of simple pendulum in small angle approximation, \(\alpha = -\omega^2 \theta\text{,}\) we find that the angular frequency of the physical pendulum is
\begin{equation}
\omega = \sqrt{ \dfrac{MgD}{I} }. \tag{13.35}
\end{equation}
(Don’t confuse this \(\omega\) with the angular speed \(d\theta/dt\text{;}\) the two are completely different quantities!) This gives frequency \(f \) to be
\begin{equation}
f = \dfrac{\omega}{2\pi} = \dfrac{1}{2\pi}\,\sqrt{ \dfrac{MgD}{I} },\tag{13.36}
\end{equation}
and the period \(T\text{,}\)
\begin{equation}
T = \dfrac{1}{f} = {2\pi}\,\sqrt{ \dfrac{I}{MgD} }.\tag{13.37}
\end{equation}
And the solution of the equation of motion is
\begin{equation}
\theta(t) = C_1\,\cos(\omega\,t) + C_2\,\sin(\omega\,t).\tag{13.38}
\end{equation}