Physics Bootcamp

Subsection 55.8.1 Fermions and Bosons

All particles in nature have spin. The magnitude \(|\vec S|\) of the spin angular momentum and the projection of the spin angular momentum vector in a direction, say the positive \(z\)-axis, \(S_z\text{,}\) of a particle of spin quantum number \(s\) are given by

The spin quantum number of every particle in nature is either an odd number multiple of \(\frac{1}{2}\text{,}\) or zero or a positive integer. For instance, the spin quantum number of electron is \(s = \frac{1}{2}\text{.}\) The spin of a proton is also \(\frac{1}{2}\text{.}\) The spin quantum number of \(Z\) boson is 0. The spin of a photon is 1.

The particles whose spins are an odd multiple of \(\frac{1}{2}\) are called fermions after the Italian physicist Enrico Fermi and the particles whose spins are zero or positive integers are called bosons after the Indian physicist Satyendra Nath Bose, who first studied their thermodynamic properties.

Subsection 55.8.2 Pauli's Exclusion principle

While studying anomalous Zeeman effect, Wolfgang Pauli found that spectroscopic lines for atoms having multiple electrons, which are all identical to each other, could be understood if he assumed that no two electrons could have the same values of all quantum numbers (Pauli actually had to introduce the fourth quantum number which turned out to be the spin quantum number proposed by Goudsmit and Uhlenbeck). Quantum numbers specify the wave function of each electron completely. So, the Pauli's principle implies that no two electrons can occupy the same space completely and have same spin projections.

Pauli's exclusion principle is actually a more general principle of nature than just applicable to electrons in atoms. Pauli exclusion principle applies to all fermions: No two fermions can be in the same quantum state. Pauli's exclusion principle does not apply to the bosons, the particles with zero or integer spins.

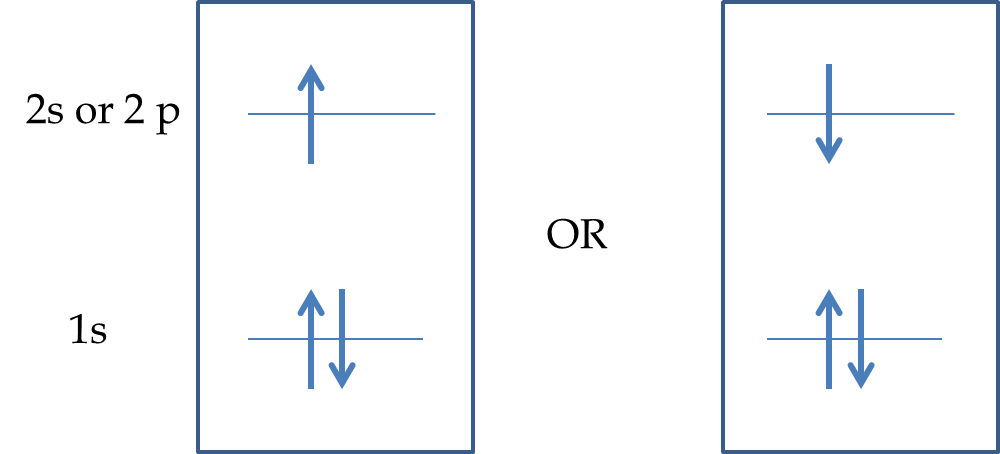
When you apply Pauli's principle to simple atoms such as lithium, which has three electrons, you can understand why lithium behaves as a one-electron system, i.e. with chemical valence of one. First note that only two electrons can in the state with \(n=1, l=0, m_l=0\text{:}\) the two differing in their \(m_s\) values, one with \(m_s = -1/2\) and the other with \(m_s = +1/2\text{.}\) The third electron has to be in the higher energy orbit with \(n=2\text{.}\) We say that two electrons in \(n=1\) are paired in spin and there is a lone electron with unpaired spin in \(n=2\) level as illustrated in Figure 55.8.1.

When Pauli's exclusion principle is applied to the wave function of a multielectron system, we require the wavefunction to be antisymmetric with respect to the exchange of particles. Suppose, we have a two electron system, e.g. the Helium atom, and let us label one electron by subscript 1 and the other electron by subscript 2. Let \(\psi_1\) be the wavefunction of electron 1, \(\psi_2\) the wavefunction of electron 2. The wavefunction \(\psi_{12}\) of the helium atom for two electrons to be in a state that one electron is in quantum state \(\alpha \equiv (n_a, l_a, m_{la}, m_{sa})\) and the other in \(\beta \equiv (n_b, l_b, m_{lb}, m_{sb})\) will be

Note that the electrons themselves are identical and we have used labels to write properties assigned to them, however, we cannot say which electron is in which state since they are identical. The antisymmetry of the wavefunction is evident when you switch the labels 1 and 2 in each term: you obtain a wave function that is minus of the wavefunction.

Also note that the antisymmetry guarantees that if \(\alpha = \beta\) then \(\psi_{12} = 0\text{.}\)

Subsection 55.8.3 Applications of Pauli's Principle

Pauli's exclusion principle can be applied anywhere we have a collection of fermions. When Pauli's principle is applied to the electrons in an atom, it helps explain the shell structure of the electron distribution around the nuclei of atoms and the fundamental reasons for the order in the periodical table.

When Pauli's principle is applied to electons in metals, we discover the Fermi level of a metal and available states in the conduction band. Pauli's principle has been applied very successfully to Astronomy. The Indian physicist Subramanyan Chandrasekhar applied Pauli's principle to predict the existence of white dwarfs, which are stars that are prevented from gravitational collapse due to the degeneracy pressure as a consequence of the Pauli's exclusion principle applied to electrons. When we apply Pauli's exclusion principle to neutrons, which also have spin \(\frac{1}{2}\text{,}\) we discover that neutrons also provide outwards pressure due to the exclusion of one neutron from occupying the same quantum state occupied by another neutron that balances immense gravitational pull.