The Rutherford scattering formula says that the scattering varies as fourth power of the sine of the angle with respect to the forward direction. In a particular experiment with alpha particles of uniform speed incident on a gold foil, 1000 alpha particles arrive every minute at an angle of $\theta = 30^{\circ}$. How many alpha particles per minute will be observed at (a) $\theta = 45^{\circ}$, (b) $\theta = 60^{\circ}$, (c) $\theta = 90^{\circ}$?
Section 52.3 Nuclear Model
Nuclear model of atom refers to the model in which most of mass of the atom is concentrated at one positive center. This model was suggested by Ruterford’s experiment. That the nucleus also contains neutral particles called neutron was discovered by Chadwick. We will discuss both these experiments in this section.
Subsection 52.3.1 The Rutherford’s Experiment
After the discovery of electrons as building blocks of atoms, J.J. Thomson proposed a model of atom, called the plum pudding model, that could explain the line spectra observed in gas discharges. In this model particles of electrons are dispersed in continuous cloud of positive charge just as resins are embedded in the pudding. The electrons in this model would resonate at their resonance frequencies explaining the absorption and emission of specific frequency light by the atom. Based on the chance discovery of Rutherford and his students Ernest Marsden and Hans Geiger we now know that this model is not correct.
Rutherford and his students were working on scattering of doubly charged alpha particles (containing two protons and two neutrons) by thin gold foil. They had noticed that the alpha particles scatter very little when they pass through a thin foil. When they looked at scattering at large angles, they were surprised to find some of the alpha particles were scattered in the backward direction. In Rutherford’s own words:
I had observed the scattering of alpha-particles, and Dr. Geiger in my laboratory had examined it in detail. He found, in thin pieces of heavy metal, that the scattering was usually small, of the order of one degree. One day Geiger came to me and said, “Don’t you think that young Marsden, whom I am training in radioactive methods, ought to begin a small research?” Now I had thought that, too, so I said, “Why not let him see if any alpha-particles can be scattered through a large angle?” I may tell you in confidence that I did not believe that they would be, since we knew the alpha-particle was a very fast, massive particle with a great deal of energy, and you could show that if the scattering was due to the accumulated effect of a number of small scatterings, the chance of an alpha-particle’s being scattered backward was very small. Then I remember two or three days later Geiger coming to me in great excitement and saying “We have been able to get some of the alpha-particles coming backward …” It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.
To explain the surprising result of any scattering at large angles Rutherford put forth a new model of atom, called the nuclear atom, in which most of its mass and all of its positive charge were concentrated in a small space as shown in Figure 52.19.
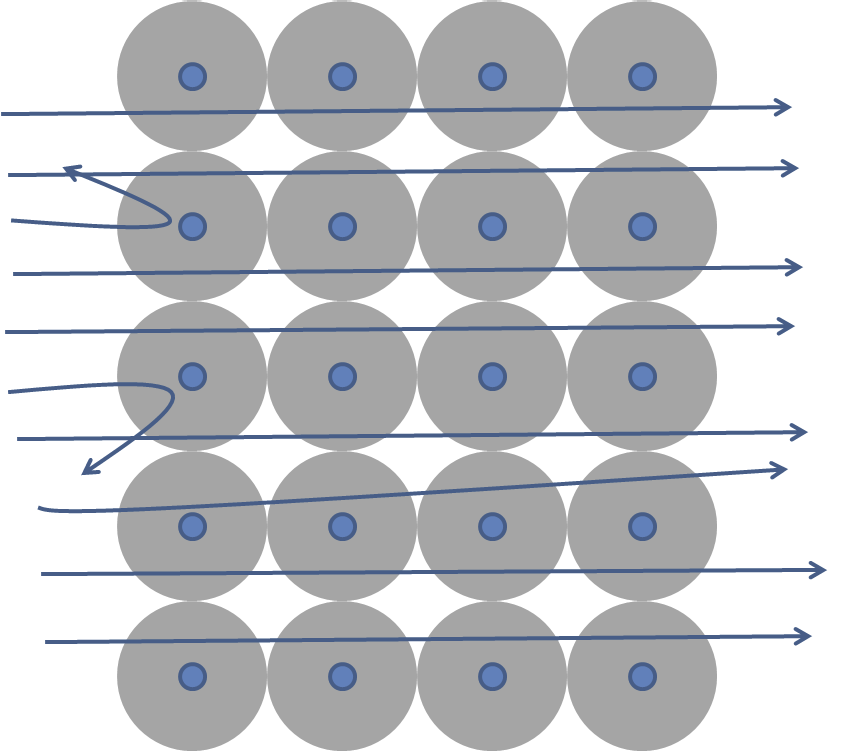
Rutherford assumed that scattering of positively charged alpha particles (charge \(+2e\)) from the positively charged nucleus (of charge \(+Ze\)) was solely due to the Coulomb force between them.
\begin{equation}
F = k \frac{(Ze)(2e)}{r^2}.\tag{52.18}
\end{equation}
Rutherford deduced a formula for the fraction of of alpha particles (\(N_\theta/N\)) that would be scattered towards an angle \(\theta\) with respect to the forward direction and detected by a detector of area \(A\) placed at a distance \(R\) from the scatterer.
\begin{equation}
\frac{N_\theta}{N} =\frac{k^2}{4}\ \frac{Z^2 w A}{R^2 K_\alpha^2 \sin^{4}(\theta/2)}, \tag{52.19}
\end{equation}
where \(w\) is the thickness of the foil and \(K_\alpha\) the kinetic energy of the alpha particles. The experiments of Rutherford and his students showed that this equation predicts the outcome of experiments perfectly as long as the kinetic energy of the alpha particles are not too great. The breakdown of this equation suggested to Rutherford that alpha particles of high enough energy were able to penetrate the nucleus which was not accounted for in the deduction of the formula.
Rutherford used the energy of the alpha particle when Eq. (52.19) breaks down to find an approximate radius of the nucleus by the nearest distance alpha particle would approach the nucleus when scattered by the threshold energy. Applying the conservation of energy to these alpha particles with kinetic energy \(K_\alpha\) when far away from the nucleus and all in terms potential energy at the nearest distance \(d_{\textrm{min}}\) of approach gives the following condition on \(d_{\textrm{min}}\text{.}\)
\begin{equation}
K_\alpha = k\frac{(Ze)(2e)}{d_{\textrm{min}}}. \tag{52.20}
\end{equation}
For heavier nuclei this requires considerably higher energy particles than was available to Rutherford. This led Rutherford to explore smaller nuclei and in 1919 he found that Eq. (52.19) broke down for aluminum target if the kinetic energy of alpha particles is above around 7.7 MeV. With \(Z=13\) we get
\begin{align*}
d_{\textrm{min}} \amp = k\frac{(Ze)(2e)}{K_\alpha}\\
\amp = 9\times 10^9\frac{(13\times 2 \times 1.67\times 10^{-19}\: e)}{7.7\times 10^6\: e} = 5.1\times 10^{-15}\:\textrm{m}.
\end{align*}
Compared to the size of an atom which would be \(\sim 10^{-10}\) m, the nucleus is 5 orders of magnitude smaller. Rutherford used the scattering equation (52.19) to determine \(Z\) of various atoms directly from experiment rather from atomic number. He also found that combined mass of all protons in a nucleus was about half as much as the mass of the nucleus. This raised the question: what contributed the rest of the mass in the nucleus? Initial guess that it may be a combination of electron and proton turned out be incorrect. If there was an electron inside a gold nucleus it will have a potential energy of
\begin{align*}
E \amp = k \frac{Z e^2}{r} = 9\times 10^9 \times \frac{79\times (1.67\times 10^{-19})^2}{10^{-14}}\\
\amp = 2 \times 10^{-12}\textrm{J} = 12\:\textrm{MeV}.
\end{align*}
However, if an electron is somehow confined in a space of dimension of a nucleus (\(\sim 10^{-14}\) m), the energy required by Heisenberg’s uncertainty will be
\begin{equation*}
K \sim \frac{(\Delta p)^2}{m} \sim \frac{\hbar^2}{m(\Delta x)^2} \sim 700 \:\textrm{MeV}.
\end{equation*}
Thus, the kinetic energy of the electron will be far greater than the binding energy provided by the Coulomb attraction. This shows that there is not enough energy to confine an electron in the nucleus. The mystery of extra mass in nucleus of atoms was solved by the discovery of neutron by James Chadwick in 1932. Neutron is neutral in charge and has the mass close to that of the mass of a proton.
Subsection 52.3.2 Chadwick’s Experiment and Discovery of Neutron
Rutherford made the suggestion in 1920 that the difference in the atomic mass and the mass due to protons in the nucleus can be made up by “neutral doublet”, or neutron, which he thought were made up of electron tightly bound to proton. Since these doublets were supposed to be neutral in charge, they would not be repelled by the nucleus and would be hard to detect. They had to be detected in an indirect way.
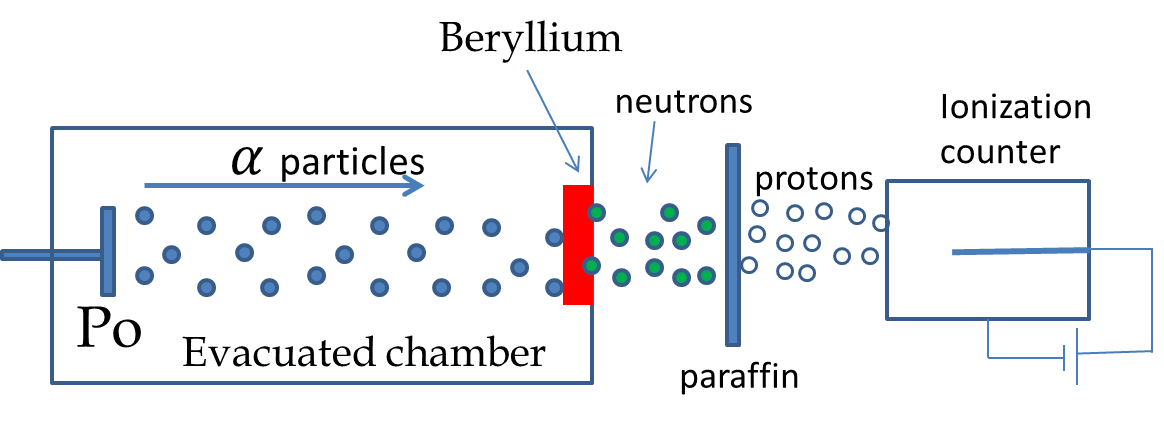
A major breakthrough came in 1930 when the German physicists Walther Bothe and Herbert Becker found that when beryllium is struck with alpha particles, it gives out a very penetrating non-ionizing radiation. They did not think that the radiation consisted of a new particle but they rather assumed that the radiation was highly energetic gamma rays. However, when French physicist couple Frédéric Joliot and Irène Joliot-Curie passed the radiation released from beryllium through a paraffin wax block they found that highly energetic protons came out. They measured speeds of these protons. They found that the energy of the protons released by paraffin wax was quite high. They too assumed the neural radiation from beryllium to be highly energetic photons and misinterpreted their results in terms of Compton effect.
James Chadwick immediately repeated the experiments of Joliet-Curies. Chadwick measured the energies of the recoiling charged particles when the radiation from beryllium struck paraffin, helium, nitrogen, and other substances. The experimental arrangement of Chadwick is shown in Figure 52.20. By an analysis of the energy of the proton released when neutrons struck the targets Chadwick was able to deduce that the neutral particles emitted by beryllium were actually a new particle which he called neutron in his paper in Nature in 1932. Chadwick was awarded Nobel Prize in physics in 1935 for his discovery of neutron.
Checkpoint 52.21. Number of Particles Scatterred in Various Angles in a Rutherford Experiment TODO.
Checkpoint 52.22. Number of Alpha Particles Scatterred by Copper and Gold in Rutherford Experiment TODO.
The Rutherford scattering formula says that the scattering varies as square of positive charge on the nucleus. Suppose same alpha particle source is incident on aluminum, copper and gold plates and the detector is set at $30^{\circ}$ to the forward direction. With aluminum foil 100 alpha particles per minute are observed in the detector. How many will be observed when the target is (a) copper, (b) gold?
Hint.
Answer.
Solution.
Checkpoint 52.23. Scatterring in Rutherford Experiment for Double Speed TODO.
The Rutherford scattering formula says that the scattering varies as inverse of the square of kinetic energy of alpha particles. In a particular experiment, alpha particles of speed $5\times 10^{6}$ m/s are incident on a thin gold foil and the detector is set at $10^{\circ}$ to the forward direction. The detector detects 1000 alpha particles per minute. How many alpha particles will be detected if the speed of the alpha particles are doubled?
Hint.
Answer.
Solution.
Checkpoint 52.24. Scatterring Protons in a Rutherford Experiment TODO.
The nucleus of copper has 29 protons and has radius $4.8\times 10^{-15}$ m. (a) What must be the speed of the alpha particles if it is to penetrate the nucleus? (b) If, instead of alpha particle, you shoot energetic protons, what must be speed of the protons at which point the proton will penetrate the nucleus?
Hint.
Answer.
Solution.
Checkpoint 52.25. Can Alpha Particles from Polonium Penetrate Beryllium Nucleus? TODO.
(a) Polonium is a source of alpha particles of energy around 5 .5 MeV. What is the speed of the alpha particles? (b) Beryllium nucleus has a loosely bound neutron that gives it an unusually large size with radius around 7 fm. Determine if 5.5 MeV alpha particles can penetrate the beryllium nucleus.

