Accelerating Frame

Section 11.1 Accelerating Frame

Subsection 11.1.1 Kinematics in Accelerating Frame

In this section I will define position, velocity, and acceleration with respect to an accelerating frame. We will also find relation between same quantities with respect two frames.

As usual, position vector is the displacement vector from the origin of a frame to the current position as shown by \(\vec r\) and \(\vec r'\) in Figure 11.1, which are positions of a particle with respect to non-accelerating and accelerating frames, respectively. Let \(\vec R\) denote vector from origin \(O\) of the non-accelerating frame to origin \(O'\) of the accelerating frame. From the triangle of vectors we have

\begin{equation} \vec r = \vec R + \vec r^{\prime}.\tag{11.1} \end{equation}

Figure 11.1. Position vectors of a point mass in two frames.

The velocity \(\vec V\) and acceleration \(\vec A\) of the accelerating frame with respect to the non-accelerating frame are simply the velocity and acceleration of origin \(O'\) of the accelerating frame, and can be obtained by successively taking time derivatives of vector \(\vec R\text{.}\)

\begin{align} \amp \vec V = \frac{d\vec R}{dt}\label{} \tag{11.2}\\ \amp \vec A = \frac{d\vec V}{dt} = \frac{d^2\vec R}{dt^2}\tag{11.3} \end{align}

The velocity \(\vec v'\) of the particle with respect to the accelerating frame is simply the rate at which position \(\vec r'\) of the particle changes with time.

\begin{equation} \vec v^{\prime} = \frac{d\vec r^{\prime}}{dt}.\tag{11.4} \end{equation}

Similarly, the acceleration \(\vec a^{\prime}\) of the particle with respect to the accelerating frame is simply the rate at which velocity \(\vec v^{\prime}\) of the particle with respect to the same frame changes with time.

\begin{equation} \vec a^{\prime} = \frac{d\vec v^{\prime}}{dt}.\tag{11.5} \end{equation}

Now, by taking successive derivatives of both sides of Eq. (11.1) with respect to time gives us the relation between velocity and acceleration of a particle in an in an inertial and a non-inertial frame.

\begin{align} \amp \vec v = \vec V + \vec v^{\prime}.\tag{11.6}\\ \amp \vec a = \vec A + \vec a^{\prime}.\tag{11.7} \end{align}

Subsection 11.1.2 Newton’s Second Law in Accelerating Frame

Newton’s second law of a point particle of mass \(m\) in an inertial frame is given by

\begin{equation*} \vec F = m\vec a \end{equation*}

where \(\vec F\) is the net force on the particle and \(\vec a\) the acceleration. This equation remains the same in all inertial frames, which are frames that have constant velocity with respect to each other. Now, we wish to find the corresponding equation of motion if the particle’s motion is observed from an accelerating frame. Let \(\vec a^{\prime}\) be the acceleration of the particle as observed from an accelerating frame. Let the acceleration of the accelerating frame with respect to the inertial frame be \(\vec A\) . By substituting Eq. (11.7) from the last section, we find that the following relation holds.

\begin{equation*} \vec F -m\vec A = m\vec a^{\prime}. \end{equation*}

Thus, in an accelerating frame one needs to add \((-m\vec A)\) to the real net force \(\vec F\) to equate the “corrected force” to mass times acceleration in that frame.

The quantity \((-m\vec A)\) acts like an additional force on the mass \(m\text{,}\) and is called a fictitious force or inertial force to distinguish it from the “real force” \(\vec F\text{.}\)

In the accelerating frame the inertial forces are felt the same way as real forces except there is no agent that applies them. The inertial force in a uniformly accelerating frame acts just like the gravitational force since it is proportional to mass. This observation led Albert Einstein to develop an alternate theory of gravitation called the general theory of relativity.

Example 11.2. Describing Motion in an Accelerating Frame.

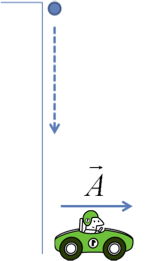
Two friends John and Jane observe the location of a building from their own frames which are accelerating with respect to each other.

In Jane’s frame John has an acceleration \(\vec A\) whose direction makes an angle \(\theta\) with respect to the direction of the building. Let the building be at a distance \(R\) from Jane who is fixed to the Earth.

Suppose at \(t=0\text{,}\) John and Jane were at the same location and their relative velocity was zero. (a) Draw a figure in Jane’s frame showing a choice of coordinates for both John and Jane supposing that the position vector of the building and acceleration vector \(\vec A\) are in the \(xy\)-plane. You can also take the \(x\)-axis to be the direction of vector \(\vec A\text{.}\) (b) Deduce the relation between the coordinates of the building in the two frame at an arbitrary time? (c) Describe the motion of the building in the two frames.

Answer.

See solution.

Solution 1. a

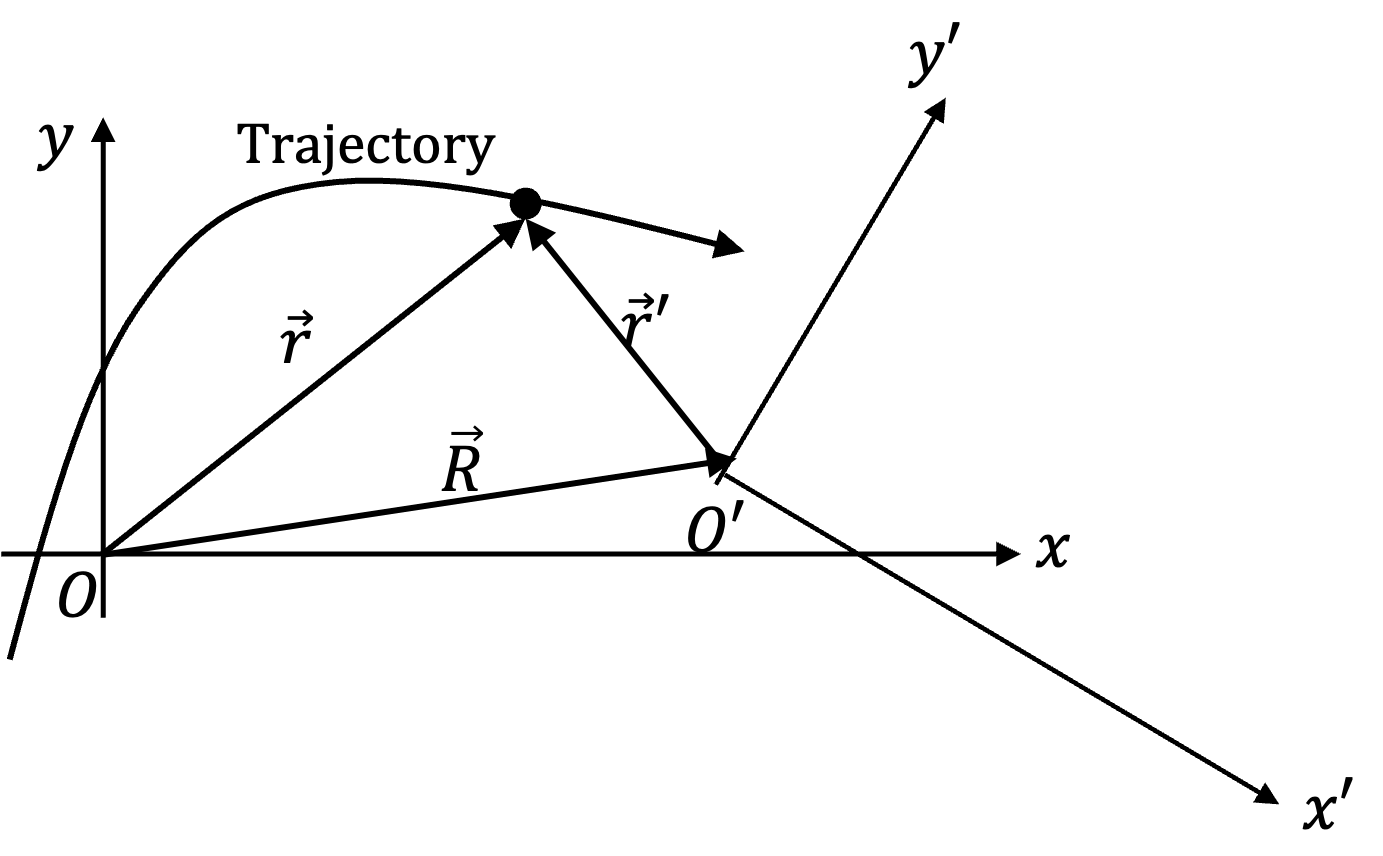
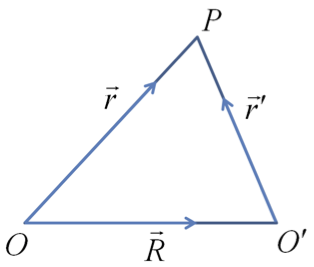
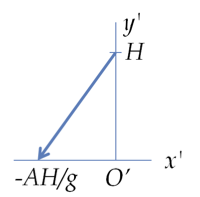
The following figure is drawn in the frame of Jane. The position of John is shown at point \(O'\text{.}\)

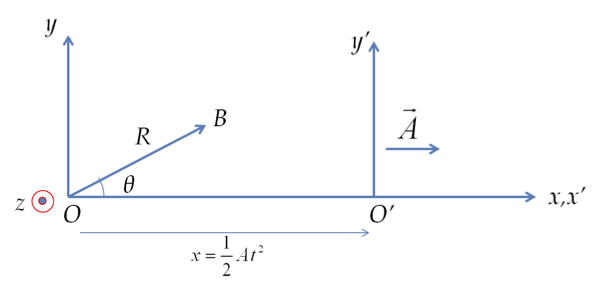
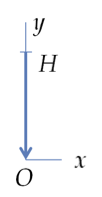
Here \(x\) is the coordinate of John at instant \(t\text{.}\) Since \(O'\) moves at a constant acceleration with respect to \(O\) and the initial speed of \(O'\) was zero at time \(t=0\text{,}\) the constant acceleration equation gives

\begin{equation*} x = \frac{1}{2} A t^2. \end{equation*}

Solution 2. b

The position of the building B in \(Oxyz\) frame is clear from the picture.

\begin{align*} \amp x_B = R\cos\theta.\\ \amp y_B = R \sin\theta. \end{align*}

The position of the same building with respect to \(O'\) will be

\begin{align*} \amp x_B^{\prime} = x_B - x = R\cos\theta - \frac{1}{2}At^2.\\ \amp y_B^{\prime} = y_B = R \sin\theta. \end{align*}

Solution 3. c

In frame \(Oxyz\) the building is at rest, but in frame \(O'xyz\) is not at rest as given by the time-dependence of its \(x\)-coordinate \(x_B\text{.}\)

Example 11.5. Apparent Weight in an Elevator.

As an example of an accelerating frame, consider a person in an elevator that is accelerating with respect to the ground with acceleration \(A\) pointed up. Suppose the person is stands on a weighing scale in the elevator.

(a) What will be the reading in the scale as observed by the person in the elevator? Note that the scale gives the value of normal force on the scale.

Suppose there is another observer outside the elevator and at rest with the ground. (b) What will be the value of the normal force by this observer?

Solution 1. a

Elevator frame.

This is non-inertial frame when the elevator has non-zero acceleration \(\vec A\) with respect to the ground. In this frame the real forces on the person are gravity (\(Mg\text{,}\) down) and normal (\(N\) unknown, up) as shown in Figure 11.6.

In this frame need to subtract \(M\vec A\text{,}\) from real forces to get the net force on the person as shown in the figure. Also, person is at rest in this frame, hence \(a'=-\text{.}\) Therefore, vertical component of Newton’s second law gives

\begin{equation*} N-Mg - MA = 0. \end{equation*}

Hence, reading in the scale will be

\begin{equation*} N = M(g+A). \end{equation*}

Solution 2. b

Ground-based frame.

In this frame forces on the person are gravity (\(Mg\text{,}\) down) and normal (\(N\) unknown, up) as shown in Figure 11.6. And person has acceleration \(a=A\) pointed up. Hence, Newton’s second law will give

\begin{equation*} N-Mg = MA. \end{equation*}

Therefore, reading in the scale will be

\begin{equation*} N = M(g+A). \end{equation*}

This is same as we found in (a).

Example 11.8. Pendulum in an Accelerating Train.

As a second example, consider a pendulum of mass \(M\) hanging from the ceiling of a train. When the train is at rest or coasting at a constant velocity, the pendulum hangs vertically. But when the train is accelerating the bob hangs at an angle \(\theta\) to the vertical. We wish to find this angle when the train’s acceleration is \(\vec A\text{.}\) We will do this problem in two frames to illustrate a non-accelerating frame and an accelerating frame shown in Figure 11.9.

Figure 11.9. Example Example 11.8. Free-body diagrams in (a) inertial and (b) non-inertial frames. Note the additional inertial force on the bob in the accelerating frame.

Equations of motion in the ground-based frame (\(\vec a \ne 0\)):

\begin{align*} \amp x\text{-component: }\ \ T\sin\theta = MA \\ \amp y\text{-component: }\ \ T\cos\theta-Mg=0 \end{align*}

Equations of motion in the train-based frame (\(\vec a' = 0\)):

\begin{align*} \amp x\text{-component: }\ \ T\sin\theta - MA=0\\ \amp y\text{-component: }\ \ T\cos\theta-Mg=0 \end{align*}

Note that the two frames yield identical relations for the equations of motion. Both frames will yield the same value for the real forces such as the tension in the string.

Exercises 11.1.3 Exercises

1. Box on an Accelerating Truck.

A box sits on a rubber floor in a truck. The driver starts the truck and increases the acceleration steadily from zero to \(5\ \textrm{m/s}^2\) in 2 seconds. If the coefficient of static friction between the box and the rubber floor is 0.2, determine if the box will slide, and if so, at what acceleration? Do this problem in the frame of the truck.

Hint.

Frame of truck is accelerating with respect to the ground.

Answer.

The box will not slide.

Solution.

In the frame of the truck, the acceleration of the box is zero when it does not slide, but the box has an additional fictitious force \(-m\vec A\text{,}\) where \(\vec A\) is the acceleration of the truck with respect to the ground. Let the \(x\) axis point in the direction of \(\vec A\) and the \(y\)-axis vertical. Then, the \(x\)- and \(y\)-components of the equation of motion of the box in the truck frame will be

\begin{align*} \amp \mu_s F_N - m A \ge 0\ \ \textrm{(if the box does not slide using }F_{s}^{\textrm{max})}\\ \amp F_N - mg = 0. \end{align*}

The given data has \(mA = 5\ m\) and \(\mu_s F_N\) = \(0.2\times 9.81\ m\) \(= 19.62\ m\text{.}\) Therefore, we do have \(\mu_s F_N > m A\text{.}\) Hence, the box will not slide.

2. Motion of a Particle in Accelerating Frame.

The coordinates of a particle in space from two frames \(Oxyz\) and \(O'x'y'z'\) are related as follows.

\begin{align*} \amp x' = x + (5\ \textrm{m/s})\ t\\ \amp y' = y + (5\ \textrm{m/s})\ t+ (2\ \textrm{m/s}^2)\ t^2\\ \amp z' = z \end{align*}

(a) Describe the relative motion of the two frames with respect to each other. (b) If a particle has a constant velocity with respect to \(Oxyz\) with components \((2\ \textrm{m/s},0,0)\text{,}\) what are the velocity and acceleration of this particle with respect to \(O'x'y'z'\text{?}\) (c) If a particle has a constant velocity with respect to \(O'x'y'z'\) with components \((2\ \textrm{m/s},0,0)\text{,}\) what are the velocity and acceleration of this particle with respect to \(Oxyz\text{?}\)

Hint.

Definition.

Answer.

See solution.

Solution 1. (a)

(a) The figure shows that the relative motions of the two frames is in the vector \(\vec R\) given by

\begin{equation*} \vec R = \vec r - \vec r^{\prime}. \end{equation*}

The \(X\text{,}\) \(Y\) and \(Z\)-coordinates of \(O'\) with respect to \(O\) are given in the problem.

\begin{align*} \amp X = x - x' = -(5\ \textrm{m/s})\ t\\ \amp Y = y -y' = -(5\ \textrm{m/s})\ t - (2\ \textrm{m/s}^2)\ t^2\\ \amp Z = z - z' =0. \end{align*}

Taking the time derivatives we obtain the components of the velocity of \(O'\) with respect to \(O\text{.}\)

\begin{align*} \amp V_x = \frac{dX}{dt} = -5\ \textrm{m/s}\\ \amp V_y = \frac{dY}{dt} = -5\ \textrm{m/s} - (4\ \textrm{m/s}^2)\ t\\ \amp V_z = \frac{dZ}{dt}=0. \end{align*}

Taking another derivative gives the components of the acceleration of \(O'\) with respect to \(O\text{.}\)

\begin{align*} \amp A_x = 0\\ \amp A_y = -4\ \textrm{m/s}^2 \\ \amp A_z = 0. \end{align*}

Therefore, the frame \(O'x'y'z'\) has the acceleration of magnitude \(4\ \textrm{m/s}^2\) towards the negative \(y\) axis. At \(t=0\text{,}\) the origins of the two frames are co-incident with the frame \(O'x'y'z'\) moving at speed \(5\sqrt{2}\) m/s at \(45^{\circ}\) with respect to the negative \(x\)-axis in the third quadrant.

Solution 2. (b)

(b) To obtain the components of the velocity we use the given position of the particle at an arbitrary time. We are given

\begin{align*} \amp v_x = \frac{dx}{dt} = 2\ \textrm{m/s} \\ \amp v_y = \frac{dy}{dt} = 0 \\ \amp v_z = \frac{dz}{dt}=0. \end{align*}

Therefore,

\begin{align*} \amp v_x^{\prime} = \frac{dx'}{dt}= \frac{dx}{dt} + 5 = 7\ \textrm{m/s} \\ \amp v_y^{\prime} = \frac{dy'}{dt} = \frac{dy}{dt} + 5 + 4 t= 5\ \textrm{m/s} + (4\ \textrm{m/s}^2) t\\ \amp v_z^{\prime} = \frac{dz'}{dt}=0. \end{align*}

The acceleration of the particle in the prime frame is

\begin{align*} \amp a_x^{\prime} = \frac{dv_x^{\prime}}{dt}= 0\\ \amp a_y^{\prime} = \frac{dv_y^{\prime}}{dt} = 4\ \textrm{m/s}^2 \\ \amp a_z^{\prime} = \frac{dv_z^{\prime}}{dt}=0. \end{align*}

Solution 3. (c)

\begin{align*} \amp v_x = \frac{dx}{dt}= -3\ \textrm{m/s} \\ \amp v_y = \frac{dy}{dt} = -3\ \textrm{m/s} - (4\ \textrm{m/s}^2) t \\ \amp v_z = \frac{dz}{dt}=0. \end{align*}

\begin{align*} \amp a_x = \frac{dv_x }{dt}= 0 \\ \amp a_y = \frac{dv_y }{dt} = -4\ \textrm{m/s}^2 \\ \amp a_z = \frac{dv_z }{dt}=0. \end{align*}

3. Box Sliding on Floor in an Accelerating Frame.

A box is sliding on a floor so that its coordinates with respect to a frame \(Oxyz\) fixed with respect to the floor are given as

\begin{align*} \amp x = (1\ \textrm{m}) + (2\ \textrm{m/s})\ t + (3\ \textrm{m/s}^2)\ t^2\\ \amp y =z=0 \end{align*}

What would be the coordinates of this box when observed with respect to another frame \(O'x'y'z'\) that has the following acceleration with respect to \(Oxyz\text{?}\)

\begin{align*} \amp A_x = 2\ \textrm{m/s}^2 \\ \amp A_y= A_z=0 \end{align*}

Assume origins \(O\) and \(O'\) coincide at \(t=0\) and the axes of the two frames are parallel with each other.

Hint.

Definition.

Answer.

See solution.

Solution.

We have shown the triangle of vectors above to give

\begin{equation} \vec {r}^{\prime} = \vec r - \vec R. \tag{11.8} \end{equation}

This leads to

\begin{equation*} \vec a^{\prime} = \vec a - \vec A, \end{equation*}

by taking two time-derivatives. In terms of components

\begin{align*} \amp a_x^{\prime} =a_x - A_x = 6\ \textrm{m/s}^2 - 2\ \textrm{m/s}^2 = 4\ \textrm{m/s}^2\\ \amp a_y^{\prime}= a_z^{\prime}=0 \end{align*}

The acceleration in the prime frame is constant in time. From Eq. (11.8), with \(V_x = A_x t\) we get the velocity in the prime frame at any arbitrary time to be

\begin{align*} \amp v_x^{\prime} =v_x - V_x =2 \ \textrm{m/s} + (6\ \textrm{m/s}^2) t- (4\ \textrm{m/s}^2) t = 2 \ \textrm{m/s} + (2\ \textrm{m/s}^2) t.\\ \amp v_y^{\prime}= v_z^{\prime}=0 \end{align*}

Integrating these with the particle at \(x' = 1\) m at \(t=0\) since \(O\) and \(O'\) coincide at \(t=0\text{.}\) \(\)

4. A Block Hanging by a Spring attached to Accelerating Elevator.

A block of mass \(m\) is hung from the ceiling of an elevator using a spring of spring constant \(k\text{.}\) Find the change in the length of the spring under the following situations. (a) Elevator going up with constant velocity, \(\vec v_1\text{.}\) (b) Elevator going down with constant velocity, \(\vec v_2\text{.}\) (c) Elevator going up with acceleration \(\vec a_1\) point up. (d) Elevator going up with acceleration \(\vec a_2\) pointed down. (e) Elevator going down with acceleration \(\vec a_3\) pointed up. (f) Elevator going down with acceleration \(\vec a_4\) pointed down.

Hint.

Definition.

Answer.

See solution.

Solution 1. (a) and (b)

(a) and (b): Since elevator is not accelerating, the situation for the block and spring system is same as on the ground. The stretching of the spring will be \(\Delta l = mg/k\text{,}\) where \(k\) is the spring constant.

Solution 2. (c)

(c) The acceleration of the elevator is pointed up and has the magnitude \(a_1\) with respect to the ground. Therefore, in the elevator frame, there will be a fictititous force on the block of magnitude \(ma_1\) and direction pointed down in addition to the weight \(mg\) of the block pointed down and the spring force \(\vec F_{\textrm{spring}}\text{.}\) In the elevator frame the block has no acceleration. Therefore, in the elevator frame,

\begin{equation*} F_{\textrm{spring}} - mg - ma_1 = 0. \end{equation*}

Writing the magnitude of the spring force as \(k\Delta l\) we find the stretching now

\begin{equation*} \Delta l = \frac{m}{k} \left( g +a_1\right). \end{equation*}

Solution 3. (d)

(d) When the acceleration of the elevator is pointed down, the fictitious force will be pointed up. This will give

\begin{equation*} F_{\textrm{spring}} - mg + ma_2 = 0. \end{equation*}

Therefore, the stretching now

\begin{equation*} \Delta l = \frac{g}{k} \left( g -a_2\right). \end{equation*}

Solution 4. (e)

(e) The direction of the movement of the accelerator does not matter - only the direction of the acceleration of the elevator goes into the force equation. Therefore, the situation is like (c).

\begin{equation*} \Delta l = \frac{g}{k} \left( g +a_3\right). \end{equation*}

Solution 5. (f)

(f) The direction of the movement of the accelerator does not matter - only the direction of the acceleration of the elevator goes into the force equation. Therefore, the situation is like (d).

\begin{equation*} \Delta l = \frac{g}{k} \left( g -a_4\right). \end{equation*}

5. Motion a Falling Ball from an Accelerating Car.

A ball is dropped from a tall building from a height \(H\text{.}\) In a frame fixed to Earth, the ball drops vertically with a constant acceleration \(g\) pointed down. The same ball is observed from a car that is accelerating with respect to the fixed frame. The acceleration of the car is pointed horizontally and away from the building and has the magnitude \(A\text{.}\)

Suppose the fixed frame has a coordinate system \(Oxyz\) whose \(y\)-axis is pointed up and the \(x\)-axis is pointed in the direction of the acceleration of the car. Let \(O'x'y'z'\) be the coordinate system whose origin is fixed to the car. The coordinate axes of the two frame are parallel to each other. The time \(t=0\) is chosen when the two origins coincide and the velocity of the car is zero with respect to the ground.

(a) Write the coordinates of the ball in \(Oxyz\) frame during the flight, i.e., before the ball hits the ground. (b) Write the coordinates of the ball in \(O'x'y'z'\) frame during the flight, i.e., before the ball hits the ground. (c) What are the trajectory of the ball in the two frames? Do the trajectory equations make sense, i.e. does the ball fall vertically in both frames?

Hint.

Definition.

Answer.

See solution.

Solution 1. (a)

(a) This is just free-fall towards the negative \(y\) axis.

\begin{align*} \amp x = 0.\\ \amp y = H -\frac{1}{2} g t^2.\\ \amp z = 0. \end{align*}

Solution 2. (b)

(b) To find the \((x',y',z')\) of the ball we first write down the coordinates \((X,Y,Z)\) of the car (\(O'\)) with respect to \(O\text{.}\)

\begin{align*} \amp Y = 0.\\ \amp Z = 0. \end{align*}

The coordinates of the ball in the two frames are related by \(\vec r = \vec r^{\prime} + \vec R\text{,}\) where \(\vec r\) is the position of the ball in \(Oxyz\text{,}\) \(\vec r^{\prime}\) is the position of the ball in \(O'x'y'z'\text{,}\) and \(\vec R\) the position of \(O'\) with respect to \(O\text{.}\)

\begin{align*} \amp x' = x-X = -\frac{1}{2} A t^2.\\ \amp y'=y-Y =H -\frac{1}{2} g t^2.\\ \amp z'=z-Z = 0. \end{align*}

Solution 3. (c)

(c) The trajectory of the ball in the frame \(Oxyz\) is straight down towards the negative \(y\)-axis. That is the trajectory is a vertically straight line since only the \(y\)-coordinate is changing with time.

The trajectory of the ball in \(O'x'y'z'\)-frame is in the \(x'y'\) plane. The ball moves from \((0,H)\) to \((-AH/g,0)\) in a straight line. The trajectory is not straight down in this frame but tilted with the angle in the third quadrant with the angle \(theta\) below the negative \(x\) axis given by \(\tan^{-1}(g/A)\text{.}\)

6. Skydiver Observed by Another Diver.

A freely falling sky diver looks at another diver directly above him that has his parachute on and finds his position in a coordinate system that has the \(y\)-axis vertically up as follows.

\begin{equation*} y = 4 + 5 t + 3 t^2. \end{equation*}

If at \(t=0\text{,}\) the freely falling person was 100 meters from the ground. Find the position of the person with his parachute on as a function of time when observed from the ground?

Hint.

Definition.

Answer.

See solution.

Solution.

Let the frame of the freely falling be \(Oxyz\) and the frame fixed to the ground be \(O'x'y'z'\text{.}\) The position of the diver with the parachute open is given in the \(Oxyz\text{.}\)

\begin{equation*} x = 0;\ \ y = 4 + 5 t + 3 t^2;\ \ z = 0. \end{equation*}

The position \(O\) of the freely falling person with respect to O will be

\begin{equation*} X = 0;\ \ Y = Y_0 + V_{0y} t - \frac{1}{2} g t^2;\ \ Z = 0. \end{equation*}

Using the \((x,y,z)\) of the parachuter P with respect to \(O\) and \((X,Y,Z)\) of \(O\) with respect to \(O'\) we can deduce the coordinate \((x',y',z')\) of P with respect to \(O'\text{.}\)

\begin{equation*} x' = 0;\ \ y' = (Y_0 + V_{0y} t - \frac{1}{2} g t^2)+(4 + 5 t + 3 t^2);\ \ z' = 0. \end{equation*}

Prev Top Next