Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 34.3 Ohm’s Law

In a wide variety of materials electric current is driven by the electric field pushing on charges such that the drift speed v of charges is proportional to the electric field \(E\) on the particle.
\begin{equation*} v = k E, \end{equation*}
where \(k\) is a constant of proportionality. Let’s multiply both sides by \(n e\text{,}\) where \(n\) is number density of conduction electrons and \(e\) the electronic charge.
\begin{equation*} nev = nek E. \end{equation*}
Left side is just the current density \(J\text{.}\) Wrting \(\sigma\) for \(nek\text{,}\) we can write this relation as a relation between current density \(J \) and electric field \(E\text{.}\)
\begin{equation} J = \sigma E. \tag{34.8} \end{equation}
This equation is called Ohm’s law, after German physicist Georg Simon Ohm (1789 - 1854). The constant of proportionality \(\sigma\) is called the conductivity of the substance. For isotropic materials, i.e. a material that does not have intrinsic preferred direction of flow for charges, \(\sigma\) is just a positive scalar quantity.
From Eq.(34.8) the unit of resistivity in SI system will be
\begin{equation*} \frac{J}{E} = \frac{\text{C}/\text{s.m}^2}{\text{N/C}}. \end{equation*}
This is a complicated combination of units. A more common way to represent it is to use unit of resistance, which is denoted by \(\Omega\text{,}\) called Ohm. In terms of \(\Omega\text{,}\) the unit is
\begin{equation*} \text{SI unit of }\sigma = \Omega\;\text{m}. \end{equation*}
A more common form of Ohm’s law between potential drop \(\Delta \phi\) across a conductor and total current \(I\) through the conductor will be derived below.
\begin{equation*} \Delta\phi = I R,\text{ or, equivalently, } V = I R, \end{equation*}
where \(R\) is resistance, to be defined below. While resisitivity is an intrinsic property of a material, resistance depends on the shape and size of the material.
Table 34.13. Resistivity of Common Materials
Material Resistivity at \(20^\circ\text{C}\) \(\alpha\,^\circ\text{C}^{-1}\)
\((\Omega\;\text{m})\)
Typical Metals
Aluminium \(2.8\times 10^{-8}\) \(4.3\times 10^{-3}\)
Copper \(1.7\times 10^{-8}\) \(6.8\times 10^{-3}\)
Gold \(2.4\times 10^{-8}\) \(3.4\times 10^{-3}\)
Iron \(9.8\times 10^{-8}\) \(5.0\times 10^{-3}\)
Lead \(21.0\times 10^{-8}\) \(3.9\times 10^{-3}\)
Mercury \(98.0\times 10^{-8}\) \(0.9\times 10^{-3}\)
Platinum \(10.0\times 10^{-8}\) \(3.9\times 10^{-3}\)
Silver \(1.6\times 10^{-8}\) \(6.1\times 10^{-3}\)
Tungsten \(4.9\times 10^{-8}\) \(4.5\times 10^{-3}\)
Zinc \(5.5\times 10^{-8}\) \(3.9\times 10^{-3}\)
Metal Alloys
Manganin \(48.0\times 10^{-8}\) \(2.0\times 10^{-3}\)
(Cu, Mn, Ni alloy)
Nichrome \(100.0\times 10^{-8}\) \(0.4\times 10^{-3}\)
(Ni, Fe, Cr alloy)
Typical Semiconductors
Pure Silicon \(2.5 \times 10^{3}\)
n-type Silicon \(8.7\times 10^{-4}\) \((n = 10^{23}\, \text{m}^{-3})\)
p-type Silicon \(2.8 \times 10^{-3}\) \((p = 10^{23}\, \text{m}^{-3})\)
Typical Insulators
Pure water \(2.5\times 10^{5}\)
Glass \(10^{10}\,\text{-}\, 10^{14}\)
Polystyrene \(\gt 10^{14}\)
Hard rubber \(10^{13}\,\text{-}\, 10^{15}\)

Subsection 34.3.1 Conductivity and Resistivity

Instead of the conductivity, \(\sigma\text{,}\) we often use the inverse of conductivity, called the resistivity, which is denoted by \(\rho\text{.}\)
\begin{equation} \sigma = \frac{1}{\rho}. \tag{34.9} \end{equation}
Temeprature-dependence of Resistivity
The resistivity \(\rho\) (or equivalently the conductivity \(\sigma\)) of a material depends on the temperature. For most metals the dependence is nearly linear over narrow ranges of temperature. Using the value of resistivity \(\rho_0\) at some reference temperature \(T_0\) in a range we express the resistivity \(\rho\) at some other temperature \(T\) near the reference temperature as follows.
\begin{equation*} \frac{\rho-\rho_0}{\rho_0} = \alpha \left( T-T_0\right). \end{equation*}
The proportionality constant \(\alpha\) is called the temperature coefficient. The temperature coefficient is small, but can be important in some applications. For instance, for copper it is \(\alpha_\text{Cu} = .00386\text{ per }^\circ\text{C}\text{.}\) If copper wire heats us by \(100^\circ\text{C}\text{,}\) you can see the resitivity change by \(38.6\%\text{.}\)

Example 34.14. Temperature from Resistance Readings.

A platinum wire is connected to a precision constant voltage source of 1.5 V and internal resistance 0.1 \(\Omega\text{.}\) Current through the wire is measured by a precision Ammeter. At \(20^{\circ}\textrm{C}\) a current of 1.010 A flows through the platinum wire. When the wire is dipped in a non-conducting fluid of unknown temperature we find that current decreases to 1.000 A. Find the temperature of the fluid.
Answer.
\(22.7^{\circ}\,\text{C}\text{.}\)
Solution.
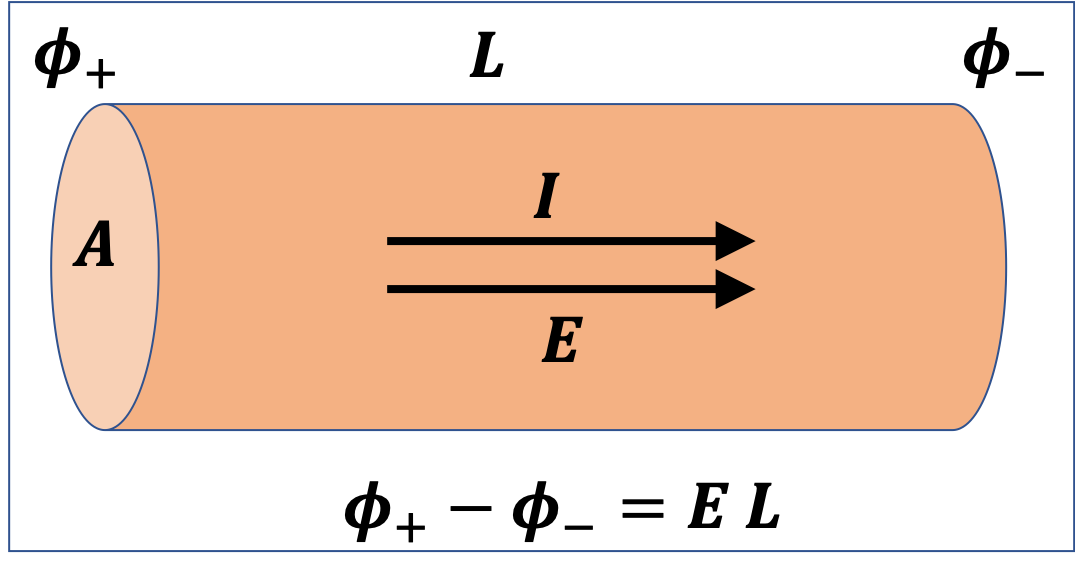
Assuming the length and area of cross-section of the wire does not vary significantly, and the difference in the current in the two situation solely comes from the variation in resistivity, we can convert the temperature-dependence formula of resistivity to temperature variation formula for resistance by using \(R = \rho\,L/A\) formula given in Eq. (34.13).
\begin{equation*} \dfrac{R-R_0}{R_0} = \alpha (T - T_0), \end{equation*}
where \(R_0\) is the resistance at \(T_0 = 20^{\circ}\)C and \(R\) the resistance at the unknown temperature. The resistance found from the experimental data is \(R+r\) and \(R_0+r\) where \(r\) is the internal resistance, which is equal to 0.1 \(\Omega\text{.}\)
\begin{align*} \amp R_0 + r = \dfrac{1.5\:\textrm{V}}{1.010\:\textrm{A}},\\ \amp R + r = \dfrac{1.5\:\textrm{V}}{1.000\:\textrm{A}} \end{align*}
From the table, the temperature coefficient for platinum is
\begin{equation*} \alpha = 3.9\times 10^{-3}\:\textrm{per}\: ^{\circ}\textrm{C}. \end{equation*}
Here \(T_0 = 20^{\circ}\)C. Hence, we have
\begin{equation*} \left. \left(\dfrac{1.5}{1.000} - \dfrac{1.5}{1.010} \right) \right/ \left(\dfrac{1.5}{1.010} -0.1 \right) = 3.9\times 10^{-3} (T - 20), \end{equation*}
which gives \(T = 22.7^{\circ}\)C.

Subsection 34.3.2 Conductance and Resistance

We now work out an important consequence of Ohm’s law that is very useful in the study of electric circuits.
Consider a uniform metallic wire of cross-section area \(A\) and length \(L\) that carries current \(I\text{.}\) Suppose we multiply Ohm’s law in Eq. (34.8) by \(A\text{.}\) This will give Ohm’s law in another form.
\begin{equation} I = JA = \sigma A E = \frac{ \sigma A }{L}\, EL = \frac{ \sigma A }{L}\,\Delta \phi.\tag{34.10} \end{equation}
The quantity \(\sigma A /L \) is called conductance and is denoted by \(G\text{.}\) Therefore, current through the wire is proportional to the potential difference across the wire.
\begin{equation} I = G\;\Delta \phi,\tag{34.11} \end{equation}
with conductance \(G\) of the cylindrical wire to be
\begin{equation} G = \frac{ \sigma A }{L}.\tag{34.12} \end{equation}
Conductance depends on geometric properties of the wire, thickness given by area of cross-section \(A\) and length \(L\text{,}\) and an intrinsic property, the conductivity, \(\sigma\text{,}\) which varies between materials and also with temperature.
The inverse of conductance is called resistance, which is denoted by \(R\text{.}\) Therefore, resitance of the wire is
\begin{equation} R = \frac{1}{G} = \frac{L}{ \sigma A } = \frac{L}{ A }\, \rho,\tag{34.13} \end{equation}
where I have replaced \(1/\sigma\) by \(\rho\text{,}\) the resistivity. This relation says that a thicker wire with larger area of cross-section will have lower resistance and a thinner wire of the same material and same length will have larger resistance. Additionally, a longer wire will have larger resistance than a shorter wire of the same material and the same thickness. One can understand this by noting that in a thicker wire there are more charge carriers in the cross-section, and therefore, there are more paths for carrying the current, and hence less resistance.
In terms \(R\text{,}\) Eq. (34.11) becomes
\begin{equation} \Delta \phi = I R,\tag{34.14} \end{equation}
which is often written as
\begin{equation*} V = IR, \end{equation*}
where \(V\) refers to voltage, which is same as the potential difference.
Equations (34.11) and (34.14) are also called Ohm’s law. Although, we have derived these expressions for a cylindrical conductor, they are applicable fo any shape.
In SI system of units, the unit of resistance is \(\text{ohm}\) (denoted by the Greek letter \(\Omega\text{.}\) According to Ohm’s law in the form given in Eq. (34.14), a current of one Ampere will flow through a wire of resistance one Ohm if a potential drop of one Volt is maintained between the ends.
\begin{equation*} 1\ \Omega = 1\ \frac{\text{V}}{\text{A}}. \end{equation*}

Example 34.15. Resistances of Wires Made from Different Metals.

(a) Find the resistances of \(1\text{-m}\) long copper wire and \(1\text{-m}\) long nichrome wire, each of diameter \(0.02\text{ mm}\text{.}\)
(b) Find the resistance of \(1\text{-m}\) long copper wire but of diameter \(0.04\text{ mm}\text{.}\)
(c) How long a copper wire would you need that has the same resistance as a \(1\text{-m}\) long nichrome wire of the same diameter?
Data: \(\rho_{\text{copper}} = 1.7\times 10^{-8}\Omega.\text{m} \text{,}\) \(\rho_{\text{nichrome}} = 100\times 10^{-8}\Omega.\text{m}\text{.}\)
Answer.
(a) \(3200\ \Omega\text{,}\) (b) \(13.5\ \Omega\text{,}\) (c) \(59\text{ m}\text{.}\)
Solution 1. (a)
We will use the fundamental formula
\begin{equation*} R = \rho\, \frac{L}{A}. \end{equation*}
Resistances of the two wires are:
\begin{align*} \amp R_{\text{copper}} = 1.7\times 10^{-8}\Omega.\text{m}\times\frac{1\ \text{m}}{\pi(0.01\times 10^{-3}\text{m})^2} = 54\ \Omega.\\ \amp R_{\text{nichrome}} = 100\times 10^{-8}\Omega.\text{m}\times\frac{1\ \text{m}}{\pi(0.01\times 10^{-3}\text{m})^2} = 3200\ \Omega. \end{align*}
Solution 2. (b)
When the thickness goes up 2-fold, the area of cross-section will go up \(2^2\) or 4-fold. This will make the resistance \(\frac{1}{4}\)-times as much.
\begin{equation*} R= \frac{54\ \Omega}{4} = 13.5\ \Omega. \end{equation*}
Solution 3. (c)
Since the two wires have the same resistance and the same thickness we have the following condition, \(R = \rho_1L_1/A = \rho_2L_2/A\text{.}\) Therefore,
\begin{align*} \frac{L_1}{L_2} \amp =\frac{\rho_2}{\rho_1} \\ \amp = \frac{100\times 10^{-8}\Omega.\text{m}}{1.7\times 10^{-8}\Omega.\text{m}} = 59. \end{align*}
This says that we would need 59 meters of copper wire for 1 m of a nichrome wire of the same thickness in order for the two wires to have the same resistance.

Example 34.16. Resistance from Resitivity, Length, and Thickness.

Find the resistances of \(10\text{ m}\) of (a) 14-gauge copper wire (diameter \(0.0642 \text{ in}\)), (b) 10-gauge copper wire (diameter \(0.102 \text{ in}\)), and (c) 14-gauge nichrome wire.
Data: \(\rho_\text{Cu} = 1.7\times 10^{-8}\:\Omega.\text{m}\text{,}\) \(\rho_\text{nichrome} = 1.0\times 10^{-6}\:\Omega.\text{m}\text{.}\)
Answer.
(a) \(8.1\times 10^{-2}\Omega\text{,}\) (b) \(3.2\times 10^{-2}\Omega\text{,}\) (c) \(4.8\Omega\text{.}\)
Solution.
Let us first convert the diameters in metric unit.
\begin{align*} D_{10} \amp = 0.102\: \text{in} = 2.59\times 10^{-3}\:\text{m}, \\ D_{14} \amp = 0.0642\: \text{in} = 1.63\times 10^{-3}\:\text{m}. \end{align*}
Use the formula of resistance of a wire.
\begin{align*} R_{14} \amp = \rho\:\frac{L}{A} \\ \amp = 1.7\times 10^{-8}\:\Omega.\text{m}\times \frac{10\:\text{m}}{\pi (0.00163/2)^2\:\text{m}^2} = 8.1\times 10^{-2}\:\Omega. \end{align*}
\begin{align*} R_{10} \amp = \rho\:\frac{L}{A}\\ \amp = 1.7\times 10^{-8}\:\Omega.\text{m}\times \frac{10\:\text{m}}{\pi (0.00259/2)^2\:\text{m}^2} = 3.2\times 10^{-2}\:\Omega. \end{align*}
For this part we need the resistivity of nichrome.
\begin{align*} R \amp = \rho\:\frac{L}{A}\\ \amp = 1.0\times 10^{-6}\:\Omega.\text{m}\times \frac{10\:\text{m}}{\pi (0.00259/2)^2\:\text{m}^2} = 4.8 \:\Omega. \end{align*}

Subsection 34.3.3 Current Through a Junction of Two Materials

Suppose you weld together a copper and a platinum wire with the same cross-section and pass a steady current through the composite conductor as shown in Figure 34.17. Since the same current \(I\) would flow through the two conductors of the same cross-sectional area, their volume current densities \(J\) would be equal.
\begin{equation*} J_\text{Cu} = J_\text{Pt}. \end{equation*}
That means
\begin{equation*} \sigma_\text{Cu} E_{\text{in Cu}} = \sigma_\text{Pt} E_{\text{in Pt}}. \end{equation*}
But since, \(\rho_{Pt} \approx 6\times \rho_{Cu}\text{,}\) i.e., \(\sigma_{Cu} \approx 6\times \sigma_{Pt}\text{.}\) That will make electric field to be lower in Cu than in Pt.
\begin{equation*} E_{\text{in Cu}} \approx \frac{1}{6} E_{\text{in Pt}}. \end{equation*}
Figure 34.17. Junction of two conductors develops a layer of charge when steady current flows through the two wires. The electric field of charges at the junction add to the electric field from the potential difference for points on the right of the junction and subtract at points on the left. This gives rise to higher electric field in platinum than in copper.
How can the electric field be different in the two metals that are welded together? You can trace the difference in the electric field to an accumulation of charges at the interface layer. As shown in Figure 34.17, if current goes from copper into platinum a layer of positive charges will build up at the interface. The excess charges at the interface create electric field that adds to the external electric field inside platinum and opposes inside copper.
We can use Gauss’s law to deduce the charge density that builds up at the interface. Let \(\sigma_{12}\) be the charge density at the interface, and \(E_1\) and \(E_2\) be the magnitudes of the electric fields in the two wires. Now imagine a Gaussian surface in the shape of a pill box about the interface as shown in Figure 34.18.
Figure 34.18. Gaussian pillbox straddling the interface used to find the excess charge density at the interface.
Note the flux is non-zero through the ends while zero through the side. Let \(A\) be the area of cross-section of the pill box at the interface. Then from Gauss’s law we obtain the following.
\begin{equation*} E_2A - E_1 A = \frac{\sigma_{12}A}{\epsilon_0} \end{equation*}
Hence, the charge density at the interface is proportional to the difference in the magnitudes of the electric field in the two wires.
\begin{equation} \sigma_{12} = \epsilon_0\left( E_2 - E_1 \right).\tag{34.15} \end{equation}
Question: What would you expect the electric fields if you weld platinum to nichrome? See if you can figure it out.

Example 34.19. Charge Density at the Interface of Two Metals.

What would be the excess charge density at the interface of copper and aluminum rods of circular cross-section of diameter \(2\) mm carrying \(12\) A current?
Solution.
Eq. (34.15) tells us the charge density in terms of electric fields. We can use Ohm’s law to express the electric fields in terms of the corresponding current densities, and then look up the resistivities from Table 34.13.
\begin{align*} \sigma_{12}\amp = \epsilon_0\left( E_2 - E_1 \right) = \epsilon_0\left( \rho_2J_2 - \rho_1J_1 \right) = \epsilon_0\left( \rho_2 - \rho_1\right)\times \frac{I}{A}\\ \amp =8.9\times 10^{-12} \frac{\textrm{C}^2}{\textrm{N.m}^2}\left(2.7-1.7 \right)\times 10^{-8} \Omega.\textrm{m}\times\frac{12\ \textrm{A}}{\pi\left( 0.001\ \textrm{m}\right)^2}\\ \amp = 3.4\times 10^{-13}\frac{C^2}{\textrm{N.m}^2}\times \Omega.\textrm{m}\times \frac{\textrm{A}}{\textrm{m}^2}\\ \amp = 3.4\times 10^{-13} \frac{\textrm{C}}{\textrm{m}^2}\ \ \left(\textrm{using}\ \textrm{A}.\Omega = \textrm{V} = \frac{\textrm{N.m}}{\textrm{C}}\right) \end{align*}

Exercises 34.3.4 Exercises

1. Resistance of a Cylindrical Shell.

A cylindrical shell made of a material of resistivity \(\rho\) has inner radius \(a\text{,}\) outer radius \(b\) and length \(L\text{.}\) Find its resistance for flow of current along its length.
Solution.
Use the formula for resistance of a wire.
\begin{equation*} R = \rho\dfrac{L}{A} = \dfrac{\rho\:L}{\pi\left( b^2 - a^2\right)}. \end{equation*}

2. Resistivity and Conductivity from Ohm’s Law Application.

A \(2\text{-m}\) wire of radius \(1.0 \text{ mm}\) of an unknown material with \(10.0 \text{ V}\) across its ends carries a current of \(0.5 \text{ A}\text{.}\) (a) Find the conductivity of the material. (b) Evaluate the resistivity of the material.
Hint.
First find the resistance, \(R\text{.}\)
Answer.
(a) \(3.18\times 10^4\ \Omega^{-1}\text{m}^{-1}\text{,}\) (b) \(3.18\times 10^{-5}\ \Omega.\text{m}\text{.}\)
Solution.
We will find the resistance by Ohm’s law and then use it to find the resistivity and conductivity.
\begin{equation*} R = \frac{\Delta \phi}{I} = \frac{10\:\text{V}}{0.5\:\text{A}} = 20 \:\Omega. \end{equation*}
(a) The conductivity is then,
\begin{align*} \sigma \amp = \frac{L}{A\:R}\\ \amp = \frac{2\:\text{m}}{(\pi\: 0.001^2\:\text{m}^2)\times 20\:\Omega}\\ \amp = 3.18\times 10^4\:\frac{1}{\Omega.\text{m}}. \end{align*}
(b) The resistivity is the inverse of conductivity.
\begin{equation*} \rho = \frac{1}{\sigma} = 3.14\times 10^{-5}\:\Omega.\text{m}. \end{equation*}

3. Resistivity and Conductivity from Ohm’s Law on a Slab.

A newly discovered material is made into a slab of width \(3.0 \text{ mm}\text{,}\) length \(2.0 \text{ cm}\text{,}\) and thickness \(1.0 \text{ mm}\text{.}\) In an experiment, it is noticed that \(2.0 \text{ mV}\) applied across its length prodices \(1.0\ \mu\text{A}\) current. (a) Evaluate the resisitivity of the material. (b) What is the conductivity of the material?
Hint.
(a) Use Ohm’s law and then use \(R\) in terms of \(\rho\text{.}\) (b) Use \(\rho= 1/\sigma\text{.}\)
Answer.
(a) \(0.3\ \Omega.\text{m}\text{,}\) (b) \(3.3\ \Omega^{-1}\text{m}^{-1}\text{.}\)
Solution 1. (a)
First we find the resistance from the current/voltage data.
\begin{equation*} R = \frac{\Delta \phi}{I} = \frac{2\text{ mV}}{1.0\ \mu\text{A}} = 2000\ \Omega. \end{equation*}
Using the Ohm’s law formula into the resistance/resistivity/conductivity formula we obtain
\begin{align*} \rho \amp = \frac{A R}{L}\\ \amp = \frac{( (0.001\times 0.003)\:\text{m}^2)\times 2000\ \Omega}{0.02\:\text{m}} = 0.3\:\Omega.\text{m}. \end{align*}
Solution 2. (b)
The resistivity is inverse of conductivity
\begin{equation*} \sigma = \frac{1}{\rho} = 3.3\: \frac{1}{\Omega.\text{m}}. \end{equation*}

4. Potential Drop Across and Electric Field in a Wire Carrying Current.

A constant voltage power source across a 12-gauge Nichrome wire (radius \(0.0404 \text{ in}\)) of length \(20 \text{ m}\) produces a current of \(3 \text{ A}\text{.}\) (a) What is the voltage across the wire? (b) Find the electric field in the wire.
Data: \(\rho_\text{nichrome} = 1.0\times 10^{-6}\:\Omega.\text{m} \text{.}\)
Hint.
Electric field magnitude wil be potential drop divided by the length.
Answer.
(a) \(18.2\text{ V}\text{,}\) (b) \(0.91\text{ V/m}\text{.}\)
Solution 1. (a)
We assume same current throughout the wire. That means same current density throughout the wire. From Ohm’s law, it means electric field is constant througout the wire. Therefore, we can get electric field by dividing the potental drop across the wire by the length of the wire.
To find the potential drop, we first work out the resistance.
\begin{align*} R \amp = \rho\:\frac{L}{A} \\ \amp = 1.0\times 10^{-6}\:\Omega.\text{m}\times \frac{10\:\text{m}}{\pi\: 0.0010262^2\:\text{m}^2} = 6.0\:\Omega. \end{align*}
Therefore, the voltage drop across the wire will be
\begin{equation*} \Delta \phi = I R = (3\:\text{A})(6.05\:\Omega) = 18.2\:\text{V}. \end{equation*}
Solution 2. (b)
The magnitude of the electric field in the wire will be
\begin{equation*} E = V/L = \frac{18.2\:\text{V}}{20\:\text{m}} = 0.91 \text{ V/m}. \end{equation*}

5. Current Density in a Wire from a Potential Difference across the Wire.

An aluminum wire of diameter \(1 \text{ mm}\) and length \(50 \text{ m}\) is connected across a \(3\text{-V}\) battery. Find the current density in the wire.
Data: \(\rho_\text{Al} = 2.7\times 10^{-8}\:\Omega.\textrm{m}\text{.}\)
Hint.
Use \(J=I/A\text{.}\)
Answer.
\(2.2\times 10^{6}\:\text{A/m}^2\text{.}\)
Solution.
The current density is related to the current and area of cross-section by \(J = I/A\text{.}\) The area of cross-section \(A\) is
\begin{equation*} A = \frac{\pi}{4} D^2 = \frac{\pi}{4} 0.001^2 = 7.85\times 10^{-7}\text{ m}^2. \end{equation*}
For current, we need resistance,
\begin{align*} R \amp = \rho \frac{L}{A} \\ \amp = 2.7\times 10^{-8}\:\Omega.\textrm{m} \times \frac{ 50\text{ m}}{7.85\times 10^{-5}\text{ m}^2 } = 1.72\ \Omega. \end{align*}
Therefore, current in the wire is
\begin{equation*} I = \frac{\Delta \phi}{R} = \frac{3\text{ V}}{1.72\ \Omega} = 1.74\text{ A}. \end{equation*}
Now, we can compute the current density.
\begin{equation*} J= \frac{I}{A} = \frac{1.74\text{ A}}{7.85\times 10^{-7}\text{ m}^2} = 2.2\times 10^{6}\:\text{A/m}^2. \end{equation*}

6. Drift Speed and Electric Field in two Metals Welded Together.

One end of Gauge 6 (diameter \(0.162\, \text{in}\)) copper wire is welded to a Gauge 6 aluminum wire. A current of \(10\, \text{A}\) passes through the composite wire. (a) Find the current density in each wire. (b) Assuming there is one conduction electron per atom for copper and one conduction electron per atom for aluminum, find the drift velocity of electrons in copper and in aluminum for the current given. (c) Why is the drift velocity in the copper wire greater than that in the aluminum wire? (d) Why do the drift velocities much smaller than common everyday experience of almost instantaneous effect of turning electrical appliances when switch is thrown?
Answer.
(a) \(7.5\times 10^5\ \textrm{A/m}^2\text{,}\) (b) \(\text{Cu } 6.03\times 10^{-5}\ \textrm{m/s}\text{,}\) \(\text{Al } 7.78\times 10^{-5}\ \textrm{m/s}\text{.}\)
Solution 1. a
Let us express the radius of the wire in the SI units.
\begin{equation*} R = \dfrac{0.162\:\textrm{in}}{2}\times \dfrac{0.0254\:\textrm{m}}{\textrm{in}} = 2.06\times 10^{-3}\:\textrm{m}. \end{equation*}
Hence, the average volume current density would be
\begin{equation*} J = \dfrac{I}{\pi R^2} = \dfrac{10\:\textrm{A}}{\pi ( 2.06\times 10^{-3}\:\textrm{m})^2} = 7.50\times 10^5\:\textrm{A/m}^2. \end{equation*}
Solution 2. b
The volume current density in a metal is also equal to the product of the charge density of conducting electrons and their drift speed. Hence, drift speed can be evaluated from current density found in (a) and charge density of conducting electrons, which will be different for the two metals.
\begin{equation*} v_d = \dfrac{J}{\rho_{\textrm{conducting}}}. \end{equation*}
Let us work out the charge density of conducting electrons in Copper.
\begin{align*} \rho_{\textrm{Cu}} \amp= \dfrac{\textrm{No. atoms}}{\textrm{m}^3}\times 1\:\textrm{e} \\ \amp = \dfrac{6.022\times 10^{23}\:\textrm{atoms}}{0.064\:\textrm{kg}} \times \dfrac{8000\:\textrm{kg}}{\textrm{m}^3} \times 1.6\times 10^{-19}\:\textrm{C} = 1.20\times 10^{10}\:\textrm{C/m}^3. \end{align*}
Hence, the drift speed of conducting electrons in copper is
\begin{equation*} (v_d)_{\textrm{Cu}} = \dfrac{J}{\rho_{\textrm{Cu}}} = \dfrac{7.5\times 10^{5}\:\textrm{A/m}^2}{1.20\times 10^{10}\:\textrm{C/m}^3} = 6.03\times 10^{-5}\:\textrm{m/s}. \end{equation*}
A similar calculation, using the density \(2700\, \text{kg/m}^3\) and atomic weight \(0.027\, \text{kg/mole}\) leads to the following drift speed in aluminum.
\begin{equation*} (v_d)_{\textrm{Al}} = 7.78\times 10^{-5}\:\textrm{m/s}. \end{equation*}
Solution 3. c
Although, the electrons move at drift speed, an electron moving out from any point of the wire is replaced by another electron entering at that point. The signal itself moves at the speed of light.

7. Electric Field in two Wires Welded Together and Carrying Current.

Two rectangular cross-section wires of copper and aluminum are welded together seamlessly. A steady current of \(50\, \text{A}\) is passed though them. The areas of cross-sections of the wires are \(4\, \text{mm}^2\) each. (a) What is the value and direction of the electric field in each wire? Assume uniform electric field. (b) What excess charges are responsible for the difference in electric field in the two materials, and where are they located?
Density of copper = \(8000\, \text{kg/m}^3\text{;}\) Density of aluminum = \(2700\, \text{kg/m}^3\text{;}\) Atomic weight of copper = 65; Atomic weight of aluminum = 27; Conductivity of copper = \(5.9 \times 10^7\, \Omega^{-1}\text{m}^{-1}\text{;}\) Conductivity of aluminum = \(3.7 \times 10^7\, \Omega^{-1}\text{m}^{-1}\text{.}\)
Answer.
(a) \(\text{Cu}\, 0.21\, \text{V/m}\text{,}\) \(\text{Al}\, 0.34\, \text{V/m}\text{.}\) (b) \(1.15\times 10^{-12}\ \textrm{C/m}^2\text{.}\)
Solution 1. a
Note the current density is same in the two wires since equal current flows past equal cross-sectional area. The magnitude of the volume current density is
\begin{equation*} J = \dfrac{50\:\textrm{A}}{4\:\textrm{mm}^2} \times \dfrac{10^6\:\textrm{mm}^2}{1\textrm{m}^2}= 1.25\times 10^{7}\:\textrm{A/m}^2. \end{equation*}
\noindent (a) Electric field is in the direction of current. The magnitude of electric field in the two metals are different because their conductivities are different according to Ohm’s law.
\begin{equation*} E = \dfrac{J}{\sigma}. \end{equation*}
Therefore electric field in Copper and Aluminum are
\begin{align*} \amp E_{\textrm{in Cu}} = \dfrac{1.25\times 10^7\:\textrm{A/m}^2}{5.9\times 10^7\:\Omega^{-1}\textrm{m}^{-1}} = 0.21\:\textrm{V/m}.\\ \amp E_{\textrm{in Al}} = \dfrac{1.25\times 10^7\:\textrm{A/m}^2}{3.7\times 10^7\:\Omega^{-1}\textrm{m}^{-1}} = 0.34\:\textrm{V/m}. \end{align*}
Solution 2. b
Imagine a box-shaped Gaussian surface straddling the interface. Let the charge collected at the interface be denoted by \(\sigma_{\textrm{face}}\text{.}\) Then we see that there must be excess charges accumulated at the interface.
Figure 34.20.
\begin{equation*} \left( E_{\textrm{in Al}} - E_{\textrm{in Cu}} \right) = \dfrac{\sigma_{\textrm{face}}\:A}{\epsilon_0}, \end{equation*}
where \(A\) is the area of cross-section of the Gaussian box. \noindent Hence, the charge density at the interface is
\begin{equation*} \sigma_{\textrm{face}} = \epsilon_0\: \left( E_{\textrm{in Al}} - E_{\textrm{in Cu}} \right) = 8.85\times 10^{-12}\times (0.34-0.21) = 1.15\times 10^{-12}\:\textrm{C/m}^2. \end{equation*}

8. Current Density and Electric Field in a Current Carrying Wire.

A cylindrical copper Gauge 6 (diameter \(0.162\, \text{in}\)) wire carries a current of \(30\, \text{A}\text{.}\) (a) Assuming that current density \(J\) is uniform throughout the cross-section, find the electric field inside the copper wire. (b) Why is the electric field not zero inside copper, which is a good conductor?
Answer.
(a) \(3.8\times 10^{-2}\,\text{V/m}\text{.}\)
Solution 1. a
From Ohm’s law we know that electric field is proportional to the volume current density. If the current density is uniform, it is equal to the current over the cross-sectional area. Hence, we have the following for the electric field.
\begin{equation*} E = \rho\:J = \rho\:\dfrac{I}{A} = 1.7\times 10^{-8}\:\Omega.\textrm{m}\dfrac{30\:\textrm{A}}{1.38\times 10^{-5}\:\textrm{m}^2} = 3.8\times 10^{-2}\:\textrm{V/m}. \end{equation*}
Solution 2. b
The electric field inside the copper wire is not zero, since it is zero only when the electrons have stopped moving while in a wire carrying a current the electrons are moving. For a steady current, the electric force due to a non-zero electric field is balanced by “retarding force” by the atoms.

9. Resistance of a Rectangular Slab in Three Different Directions.

A rectangular slab of copper has dimensions as shown in the figure. Find resistance in the three directions.
Figure 34.21.
Answer.
\(1.13\times 10^{-1}\,\Omega\text{,}\) \(6.38\times 10^{-4}\,\Omega\text{,}\) \(2.83\times 10^{-4}\,\Omega\text{.}\)
Solution 1. a
The resistance formula tells us that resistance is proportional to the length and inversely proportional to the cross-sectional area. Both length and cross-sectional area depend upon the direction of the current. Hence, we have the following values of the resistance depending on the direction in which we pass the current even when the material is homogeneous and the resistivity is independent of direction.
\begin{equation*} R = 1.7\times 10^{-8}\:\Omega.\textrm{m}\times \dfrac{40\times 10^{-6}\:\textrm{m}}{(2\times 10^{-6}\:\textrm{m})(3\times 10^{-6}\:\textrm{m})} = 1.13\times 10^{-1}\:\Omega\text{.} \end{equation*}
Solution 2. b
\begin{equation*} R = 1.7\times 10^{-8}\:\Omega.\textrm{m}\times \dfrac{3\times 10^{-6}\:\textrm{m}}{(2\times 10^{-6}\:\textrm{m})(40\times 10^{-6}\:\textrm{m})} = 6.38\times 10^{-4}\:\Omega\text{.} \end{equation*}
Solution 3. c
\begin{equation*} R = 1.7\times 10^{-8}\:\Omega.\textrm{m}\times \dfrac{2\times 10^{-6}\:\textrm{m}}{(3\times 10^{-6}\:\textrm{m})(40\times 10^{-6}\:\textrm{m})} = 2.83\times 10^{-4}\:\Omega\text{.} \end{equation*}
PrevTopNext
Found typo?