Archimedes’ Principle

Section 17.6 Archimedes’ Principle

Archimedes’s principle refers to the upward force of buoyancy that results when a body is submerged in a fluid, whether partially or wholly. We will find that the main reason for buoyancy is the difference in pressure at different depths. Due to buoyancy, an object appear lighter when submerged. The difference of actual weight of a body and the buoyancy force is called the apparent weight of the body.

Let’s look at a rectangular block fully submerged in water as in Figure 17.31. The pressure from the sides exert forces on the block - they cancel each other out. But, since the pressure at the top surface is less than the pressure at the bottom surface, the forces from those pressures will have a left over upward pointing net force. This is the buoyancy force.

Figure 17.31. The buoyancy force on the block occurs due to pressure increasing with depth. The net upward force is the buoyancy force, whose magnitude would be \(F_b = p_2\ A - p_1\, A = (p_2-p_1)A\text{.}\) The horizontal forces, \(p_3A,\ p_4A,\ p_5A,\ p_6A\) are balanced - they are not involved in buoyancy.

The buoyancy force is pointed up and has the magnitude

\begin{equation*} F_b = p_2\ A - p_1\, A = (p_2-p_1)A. \end{equation*}

Writing the pressure at a point in the fluid as

\begin{equation*} p = p_0 + \rho\,g\,h, \end{equation*}

where \(p_0\) is the atmospheric pressure, we can see that

\begin{equation*} p_2-p_1 = \rho_w g h. \end{equation*}

where \(\rho_w\) is the density of water and \(h \) the height of the block. Therefore, we can write the force of buoyancy as

\begin{equation*} F_b = (p_2-p_1)A = \rho_w g h A = \rho_w g V, \end{equation*}

where \(V\) is the volume of the block. Since the block is fully submerged, \(V\) is also the volume of the fluid that was displaced by the block. We see that \(\rho_w V\) is the mass of the water corresponding to the volume of water that was displaced by the submerged block. Therefore, we write the buoyancy force alternately as

\begin{equation} \vec F_b = \text{Weight of displaced fluid, pointed up}.\tag{17.18} \end{equation}

This is the statement of the Archimedes’ principle. We should that this works also for the partially submerged block. When the block is partially submerged, the volume will not be the volume of the entire block, but of only the part that is actually submerged.

Figure to the right shows a partially submerged block of full height \(h\text{,}\) of which only the height \(h_s\) is submerged. Forces from the sides again cancel out, and the upward buiyancy force is

\begin{align*} F_b \amp = (p_2-p_1)A = \rho_w g h_s A, \\ \amp = W_{\text{displaced fluid}}. \end{align*}

Now, \(Ah_s\) is not the volume of the block, but only the part that is submerged. That is the part that equals the volume of fluid that was displaced. Therefore, once again, the buoyancy is the weight of the displaced fluid.

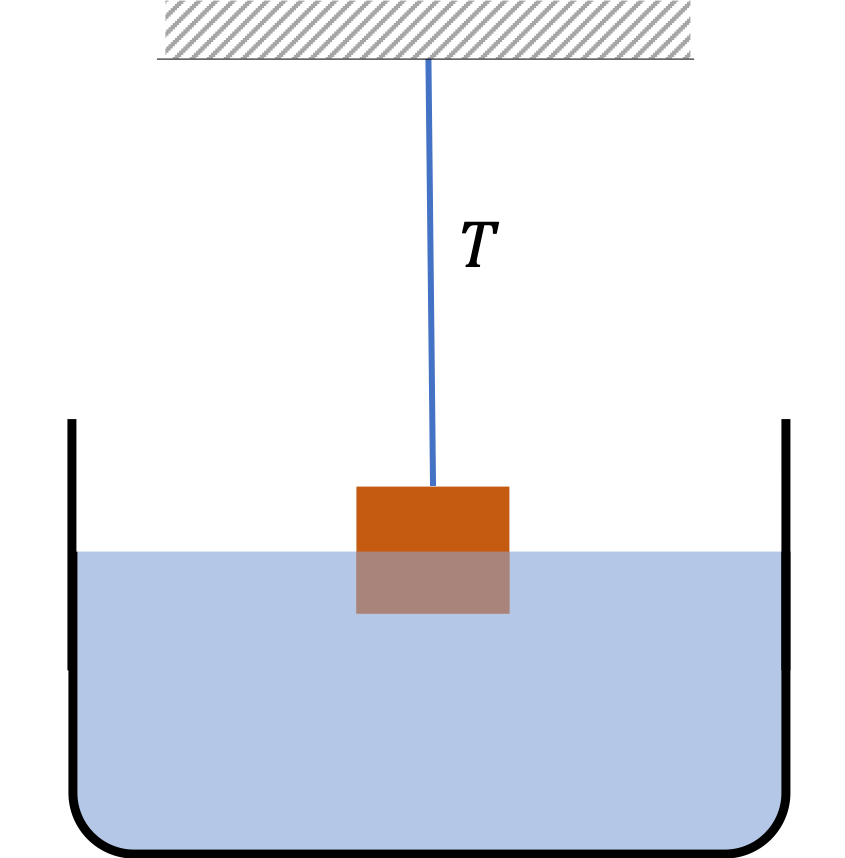
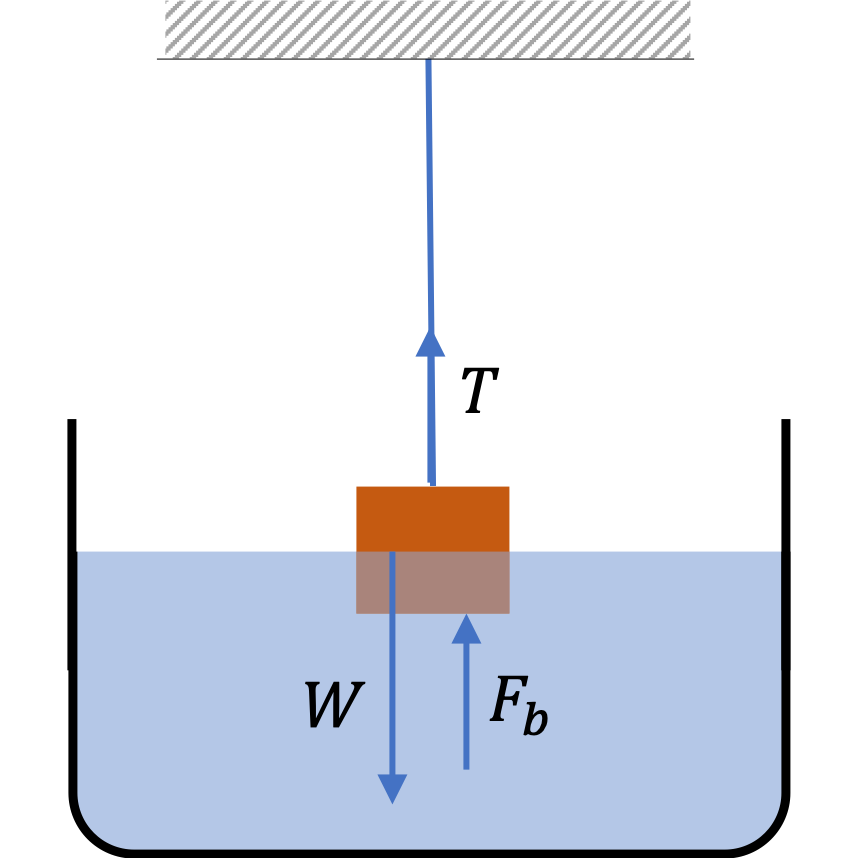
Example 17.32. Density from Apparenet Weight of Fully Submerged Body.

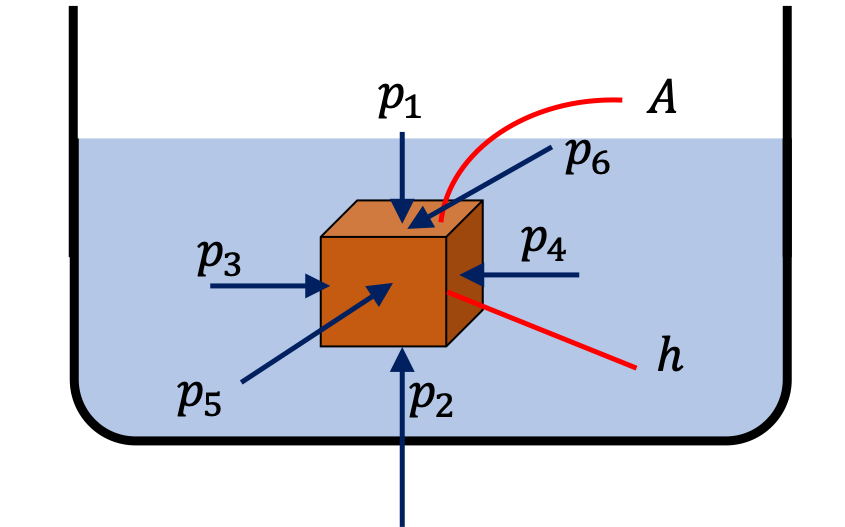
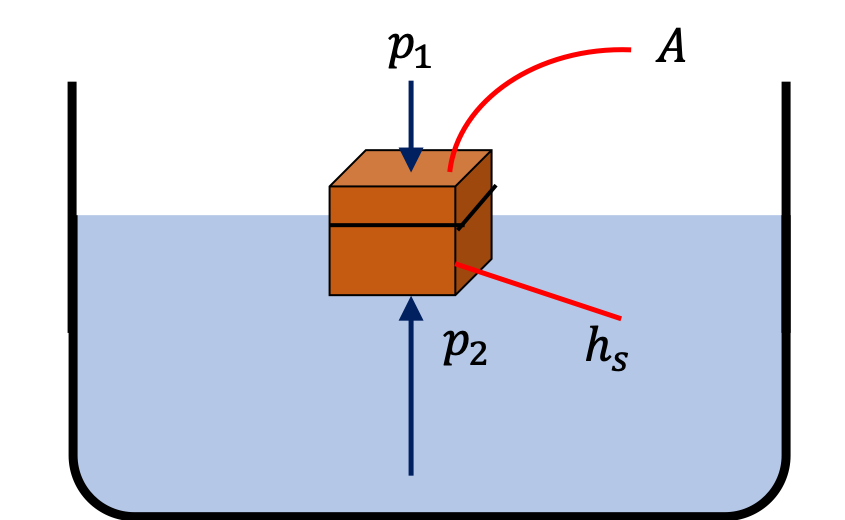
We tie a block of a material of density higher than the density of water to a thin thread and measure the tension in the thread as the block is lowered in water. When the block is in air, the tension is \(50\text{ N} \) and when fully submerged, the tension is \(40\text{ N} \text{.}\) What is the density of the material if the density of water is \(1000\text{ kg/m}^3\text{.}\)

Answer.

\(5000\text{ kg/m}^3 \)

Solution.

Let \(W \) be the tension in air, and \(W'\) the tension when fully submerged in water. Let \(V \) be the volume of the block, \(\rho_0\) the density of water, and \(\rho\) the density of the block.

From the two experiments we can write the following relations.

\begin{align*} \amp W = V\rho g, \\ \amp W' = W - F_b, \\ \amp F_b = V\rho_0 g. \end{align*}

The volume of the block can be written as

\begin{equation*} V = \dfrac{W}{\rho g} \end{equation*}

Therefore,

\begin{equation*} W' = \dfrac{W}{\rho} \left( \rho - \rho_0 \right). \end{equation*}

Therefore,

\begin{equation*} 1- \dfrac{\rho_0}{\rho} = \dfrac{W'}{W}, \end{equation*}

which gives

\begin{equation*} \rho = \dfrac{W}{W-W'}\, \rho_0. \end{equation*}

Now, putting in the numbers we get

\begin{equation*} \rho = \dfrac{50}{10}\times 1000 = 5000\text{ kg/m}^3. \end{equation*}

Example 17.33. Floating Steel Container in Water.

A \(1\text{-mm}\) thick steel sheet is made into a cylindrical cup of outer radius \(10\text{ cm}\) and height \(30\text{ cm}\) with one end sealed and the other end open. It is then placed in water with the closed end first. How much of the cup stays above water?

Data: density of water = \(1.0\text{ g/cm}^3\text{,}\) density of steel = \(8.0\text{ g/cm}^3\text{.}\)

Answer.

\(24.4\text{ cm}.\)

Solution.

Let \(h\) be the height of the cylinder above water and \(H\) its total height. Let \(r_\text{out}\) be the outer radius, \(r_\text{in}\) the inner radius, and \(t \) the thickness. Let us denote the density of steel by \(\rho\) ad the density of water by \(\rho_0\text{.}\)

The force of buoyancy on the container will balance the weight of the container since the acceleration of the container is zero. To find an expression for the weight of the container, we figure out the volume of the material used to make the container by adding the volume of the side and the bottom.

\begin{equation*} V = \left( \pi r_\text{out}^2 - \pi r_\text{in}^2 \right)\, H + \pi r_\text{in}^2 t. \end{equation*}

Therefore, weight of the container is

\begin{equation} W = \rho V g.\tag{17.19} \end{equation}

Recall the magnitude of the buoyancy force is equal to the weight of the displaced fluid. Since \(H-h\) of the height is under water, this gives the following for the magnitude of the buoyancy force.

\begin{equation} F_b = \rho_0\, \left[ \pi r_\text{out}^2 (H-h)\right]\, g. \tag{17.20} \end{equation}

Equating \(W\) with \(F_b\) gives the equation,

\begin{equation*} \rho_0\, \left[\pi r_\text{out}^2 (H-h)\right]\, g = W, \end{equation*}

which can be solved for \(h\)

\begin{equation*} h = \dfrac{W}{ \rho_0 \pi r_\text{out}^2 g}. \end{equation*}

Putting in the full expression for \(W\) from Eq. (17.19), and setting \(r_\text{out} = R = r_\text{in}+t\)

\begin{equation*} H-h = \dfrac{\rho}{\rho_0} \left[ (1 - x) H + x t \right], \end{equation*}

where

\begin{equation*} x = \left( 1- \dfrac{t}{R}\right)^2. \end{equation*}

Now, we use the numerical values in \(\text{cm}\) units for length, we get

\begin{align*} x \amp= \left( 1- \dfrac{0.1}{10}\right)^2 = 0.99^2 = 0.9801. \end{align*}

Therefore, we get

\begin{align*} H-h \amp = \dfrac{8.0}{1.0} \left[ (1 - 0.9801) \times 30 + 0.9801\times 0.1 \right] \\ \amp = 5.6\text{ cm}. \end{align*}

Hence,

\begin{align*} h \amp = H - 5.6\text{ cm} = 24.4\text{ cm}. \end{align*}

Exercises Exercises

1. Pushing Down a Ball Filled with Air into Water.

A plastic spherical ball of negligible mass and filled with air has a radius of \(10\text{ cm}\text{.}\) A boy pushes the ball in water till quarter of its volume is submerged. How much force the boy must apply to keep the ball so submerged? Assume negligible change in the volume of the ball.

Hint.

Balance the required force by the force of buoyancy. When computing buoyancy, only the volume of the displaced fluid matters.

Answer.

\(10.3\text{ N}\text{,}\) down.

Solution.

Let \(F\) be the force by the boy. This force on the ball balances the buoyancy force on the ball. We ignore the weight of the ball.

\begin{equation*} F = F_b, \end{equation*}

with

\begin{equation*} F_b = \dfrac{V}{4}\,\rho_w\, g. \end{equation*}

Therefore,we have

\begin{align*} F \amp = \dfrac{1}{4}\,\dfrac{4}{3} \pi R^3 \rho_w\, g, \\ \amp = \dfrac{1}{3} \pi\times 0.1^3 \times 10^3\times 9.81 = 10.3\text{ N}. \end{align*}

The direction of this force is down.

2. Apparent Weight of a Brass Block Half Submerged in Water.

A block of brass of mass \(800\text{ grams}\) is attached to a string and hung from a support. The block is then placed so that half of the block is submerged in the water. What is the tension in the string?

Data: density of brass = \(8.6\text{ g/cc}\text{,}\) density of water = \(1.0\text{ g/cc}\text{.}\)

Hint.

Balance tension, buoyancy, and weight.

Answer.

\(7.4\text{ N}.\)

Solution.

Let \(\rho \) denote the density of brass and \(\rho_0 \) the density of water. There are three forces on the block: the weight \(Mg\) of the block pointed down, the tension \(T\) in the string pointed up, and the buoyancy \(F_B \) pointed up. The forces are in balance.

\begin{equation*} F_B + T = Mg. \end{equation*}

Half of the volume \(V\) of the block is in water, which we will write as \(V = M/\rho\text{.}\) Therefore, the buoyancy is

\begin{equation*} F_B = \frac{1}{2}V \rho_0 g = \frac{1}{2} \frac{M}{\rho} \rho_0 g. \end{equation*}

The two equations give the magnitude of the tension in the string to be

\begin{equation*} T = \left[ 1 - \frac{1}{2} \frac{\rho_0}{\rho} \right]\ M g. \end{equation*}

Now, putting in the numbers we get

\begin{align*} T \amp =\left[ 1 - \frac{1}{2} \times \dfrac{1.0\ \text{g/cc}}{ 8.6\ \text{g/cc}} \right]\ 0.8\ \text{kg} \times 9.81 \text{m/s}^2 \\ \amp = 7.38\text{ N}. \end{align*}

3. Thickness of a Closed Cubical Aluminum Box Floats in Water.

A closed cubical box of side \(a = 16\text{ cm}\) made of aluminum sheet of unknown thickness \(t\) floats in water with \(\dfrac{1}{4}\) of it above the surface of water. Find the thickness of the sheet.

Data: Density of aluminum = \(2.7\text{ g/cc} \text{,}\) dnesity of water = \(1.0\text{ g/cc}\text{.}\)

Hint.

Balance weight by the buoyancy.

Answer.

\(0.256\text{ cm}. \)

Solution.

Let \(\rho\) denote the density of aluminum and \(\rho_0\) the density of water. Let us denote the fraction of the block submerged by \(f\text{,}\) which has the value \(\frac{3}{4}a = 12\text{ cm}\) here. Balancing the weight of the box by the buoyancy force gives

\begin{equation} Mg = f a^3 \rho_0 g,\tag{17.21} \end{equation}

where

\begin{equation*} M = (4 a^2 t + 2 (a-2t)^2 t) \rho. \end{equation*}

Let us define a simple variable to solve for.

\begin{equation*} x =\frac{t}{a}, \end{equation*}

and expanding Eq. (17.21) to find

\begin{equation*} x^3 - x^2 + 0.75 x = \frac{f\rho_0}{8 \rho}. \end{equation*}

Putting in the numerical values given we find that we need to solve the following cubic equation.

\begin{equation*} x^3 - x^2 + 0.75 x - 0.01157 = 0. \end{equation*}

where I have kept the extra digits. The final answer will be rounded to two significant digits. I put this equation in Mathematica and found that there is only one real value, the other two solutions are complex numbers.

\begin{equation*} x = 0.01575. \end{equation*}

Rounding off to two significant digits we find the thickness in terms of the side of the cube to be

\begin{equation*} t = 0.016\; a = 0.016\times 16\text{ cm} = 0.256\text{ cm}. \end{equation*}

4. A Cubical Box with Open End Floating in Mercury.

A cubical box of side 10 cm made of steel has an open side. With open side of the box up, 90\% of the box floats in mercury. How much of the box will float if 200 gram of load is put inside the box?

Solution.

We already know that that only 1 cm is above the mercury. Now, if we put 200 g more, then the additional buoyancy we need will come from the decrease in this 1 cm. Let the decrease be \(\Delta h\text{.}\) This additional buoyancy should balance the additional weight. Let us denote the area of the base by \(A\text{,}\) the density of the mercury by \(\rho\text{,}\) the additional mass by \(m\text{.}\) Then we have

\begin{equation*} (A \Delta h) \rho g = mg. \end{equation*}

This gives

\begin{equation*} \Delta h = \frac{m}{A \rho} = \frac{0.2\ \textrm{kg}}{0.01\ \textrm{m}^2 \times 13,600\ \textrm{kg/m}^3} = 0.147\ \textrm{cm}. \end{equation*}

With the load the container will have only 1 cm - 0.147 cm = 0.953 cm above mercury.

5. (Calculus) Work for Pushing a Wooden Block Under Water.

A cubic wooden block (density \(0.9\)) of side \(5\text{ cm}\) is placed in water.

(a) How much of the block is under water?

(b) (Calculus) The block is then pushed down by a force which balances the increase in the buoyancy force at each instant. What is the total work needed to fully submerge the block?

Hint.

(a) Balance weight by buoyancy force, (b) You will find that the force when an amount \(y\) is pushed in, depends on \(y\text{.}\) You can integrate over \(y\) to get the force - similar to the way you get the work by the spring force.

Answer.

(a) \(4.5\text{ cm}\text{,}\) (b) \(0.003\text{ J}\text{.}\)

Solution 1. (a)

(a) Let \(a\) denote the side of the cube, \(\rho\) the density of the wood and \(\rho_0\) the density of water. Let \(h_0\) be the height submerged when freely floating. Balancing the buyoancy force with the weight of the block gives

\begin{equation*} (a^2 h_0) \rho_0 g = a^3 \rho g. \end{equation*}

Solving for \(h_0\) we get

\begin{equation*} h_0 = \left( \dfrac{ \rho}{\rho_0} \right) a. \end{equation*}

Putting in the numbers given we find the height submerged is

\begin{align*} h_0 \amp = \left( \dfrac{ 0.9\ \text{g/cc}}{1.0\ \text{g/cc}} \right) 5\ \text{cm}\\ \amp = 4.5\ \text{cm}. \end{align*}

Solution 2. (b)

(b) The force needed to push in the block depends on the level of submersion.

For instance, suppose you choose a coordinate system such that \(y\) axis is pointed up and the center of the block is at the origin when the block is submerged by \(h_0\text{,}\) then the force to push in will depend on the \(y\)-coordinate of the center of the block. The \(y\)-component of the force applied will be

\begin{equation*} F_y = - (a^2 y) \rho_0 g. \end{equation*}

The change in the \(y\)-coordinate to fully submerge the block will be

\begin{equation*} \Delta y = -(a-h_0). \end{equation*}

The work done by the applied force to fully submerge the block can be obtained by the area under the curve or integral. Doing the integral for force that varies with displacement gives

\begin{align*} W \amp = \int _0^{\Delta y} F_y dy = \frac{1}{2} a^2 \rho_0 g (\Delta y)^2\\ \amp = \frac{1}{2} a^2 (a-h_0)^2 \rho_0 g. \end{align*}

Putting in the numbers we find

\begin{align*} W \amp = \frac{1}{2} \times 0.05^2 (0.05-0.045)^2 \times 1000 \times 9.81 \\ \amp =3.07\times 10^{-4}\ \text{J}. \end{align*}

Prev Top Next